Оптимальная форма ротора гиродина в классе конических тел

DOI:

При разработке шагающих роботизированных систем, таких как AnyWalker [2; 4], и систем стабилизации их движения на основе гиродинов [3; 5] возникает проблема выбора конструкции гиродинов. В частности, необходимо выбрать форму ротора гиродина таким образом, чтобы обеспечить максимальную эффективность работы гиродина. Эффективность обусловливается в основном моментом импульса ротора относительно оси вращения ротора. При фиксированной массе ротора момент импульса можно увеличить за счет увеличения скорости его вращения либо за счет увеличения момента инерции ротора гиродина относительно оси его вращения путем перераспределения массы «подальше» от оси. Как увеличение скорости, так и увеличение момента инерции ведет к увеличению внутренних напряжений в материале ротора. Таким образом, возникает задача выбора скорости вращения и формы ротора гиродина для того, чтобы максимизировать момент импульса при выполнении условий прочности. Поставленную задачу следует рассматривать при дополнительных ограничениях на размер и массу ротора, поскольку эти ограничения являются следствием ограничений на размеры и массу конструкции.

1. Постановка задачи

Перед тем, как непосредственно перейти к математической постановке задачи исследования, рассмотрим математическую модель упруго-деформированного состояния ротора, приведенную в работе [1].

Ротор гиродина является телом вращения, толщина которого зависит только от расстояния r до оси вращения, г Е [0,R]. Поверхность ротора задана вращением кривых z = ±z(r) вокруг оси. Иными словами, функция z(r) определяет профиль ротора. Толщина ротора на расстоянии r от оси равна 2z(r).

Ротор будем считать тонким, и поэтому пренебрегаем перемещениями и механиче- скими напряжениями в направлении, параллельном оси вращения ротора. В теле ротора образуются поля нормальных напряжений: радиальное от и кольцевое ot. В силу симметрии все силы и напряжения будут функциями расстояния r от оси вращения.

Когда ротор раскручен, он претерпевает деформации, в результате которых произвольная точка А смещается в радиальном направлении в точку А ’ (см. рис. 1).

Поле деформации в точке А определяется вектором АА ‘ . В силу радиальной симметрии длина этого вектора зависит лишь от радиуса г = | ОА | . Определим функцию деформации и : [0, R] ^ R , как длину вектора смещения: и(г) = | АА ‘ | . Поле деформаций однозначно описывается этой функцией.

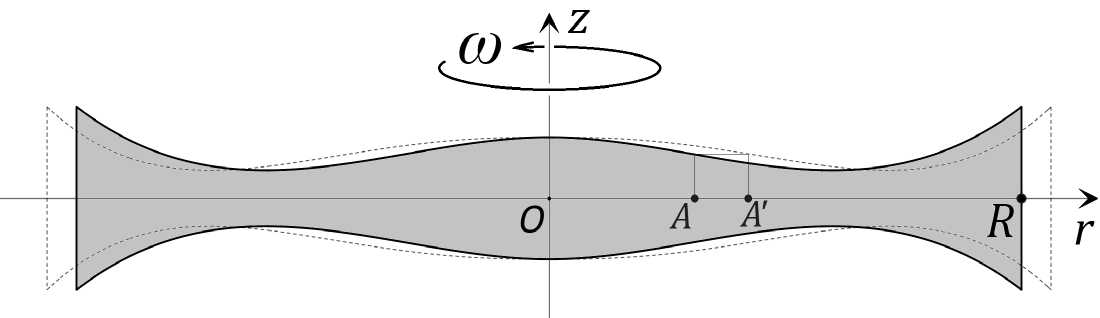
Рис. 1. Профиль ротора и его деформация

Функция - удовлетворяет уравнению упруго-деформируемого состояния [1]:

, - ₂ f z^^- + Гу^- + rz^ + ц ^и - z- ^ + рш ² ?z = 0, г е (0; R).   (1)

1 — ц ² у dr dr dr     dr ²     dr r}

Связь между полем деформаций и полями напряжений описывается уравнениями [1]

( ^O r = 1 - ^ 2 ($ ⁺ Ц ⁷ ) , I ^o t = 1 - ^ 2 ⁽ц§ ^{+ 7 )} .

Здесь R обозначает радиус ротора; ш — угловая скорость вращения ротора; р — плотность; E — модуль Юнга; µ — коэффициент Пуассона материала ротора.

Положительное значение напряжения о _т соответствует растяжению элементарного объема в радиальном направлении, а отрицательное — сжатию. Аналогично знак o _t определяет растяжение/сжатие элементарного объема в тангенциальном направлении.

В силу отсутствия воздействия со стороны внешней границы o _r (R) = 0 . Ввиду радиальной симметрии центр ротора не смещается, то есть -(0) = 0 . Поэтому уравнение (1) относительно функции - дополняется следующими краевыми условиями:

u(0)=0,    d^- (R) + ц ^^ = 0.                     (3)

dr        R

Краевая задача (1), (3) ставится для каждой положительной на (0, R) функции z е е С 1 [0, R] . Классическим решением краевой задачи (1), (3) будем называть функцию

- е С0[0,R] ПС1 (0, R] ПС2(0, R), которая удовлетворяет соотношениям (1) и (3).

Максимальное механическое напряжение, соответствующее растяжению элементарных объемов, в теле ротора, заданного полутолщиной z раскрученного до угловой скорости ω , описывается функционалом:

S д, P ,E, ц (ш ,z( • ) ) = sup max (o _r (ж), о^ ж) ) .                        (4)

ж £ [0,Я]

В формуле (4) отсутствует модуль, поскольку мы считаем, что разрушение материала может происходить только из-за растяжения. Это обусловливается как постановкой задачи, так и тем, что предел прочности на сжатие существенно выше, чем предел прочности на растяжение.

При заданном материале, массе т и радиусе R ротора гиродина требуется подобрать его форму z(г) в заданном классе функций У С С 1 [0, R] с дополнительным условием

4пр / г z(г) dr = т и угловую скорость вращения ω с целью максимизации момента импульса

L (w ,z( • )) = 4 npw / г ³ z(г)dг, 0

учитывая при этом конечную прочность материала ротора:

s^p,e,^(^. :(• П 6 И, где [ст] обозначает максимально допустимое напряжение материала ротора. Определим множество

Kr^e^u = {( w,z) G R х У ^: выполнены (5) и (6) }•

Это множество будем называть множеством, удовлетворяющем условию прочности, или множеством прочности.

Основная задача состоит в том, чтобы найти максимум функционала момента импульса L (w,z0) на множестве Евт^и :

M (R, т, р , Е, [ ст ], р )

max        L(w, z (•)) , y,y)EKR,m,p,E>w

предъявить максимизирующую пару ( w ,z( ^ )) G K R,_m, _p ,_E,[ _CT ], _p , задающую профиль z оптимального ротора и его оптимальную угловую скорость вращения

В дальнейшем, в настоящей статье, будем считать, что р = 7800 м 3 , [ ст ] = 147 МПа, Е = 200 ГПа, что соответствует стали. Зафиксируем т = 2 кг, R = 0,12 м, что соответствует параметрам разрабатываемой установки [5]. Для упрощения обозначений зависимость от этих пяти параметров в дальнейшем будем опускать. Для стали коэффициент Пуассона р = 0,3 , однако, нас интересует вопрос зависимости задачи от параметра р . Поэтому будем считать, что р G ( — 1,1) , несмотря на то, что изотропных материалов с коэффициентами Пуассона р > 0, 5 , по-видимому, не существует.

В качестве класса функций У возьмем многочлены степени не выше первой, задающие конические тела вращения. Для этого класса функций уравнение (1), вообще говоря, не разрешимо аналитически, так же как и в общем случае, что вынуждает нас пользоваться численными методами, даже в этом относительно простом случае. В этом смысле мы не ограничиваем общности предлагаемого подхода. С другой стороны, мы избегаем ряд технических сложностей, например, проверка условия положительности z(г) при г G (0, R) упрощается, результаты вычислений можно представить более наглядно. Кроме этого, конические роторы проще в изготовлении.

аналитически решить задачу не удается, кроме некоторых частных случаев, например, b = 0 или a = 0 . По-видимому, общего аналитического решения в этом классе нет, поэтому будем решать задачу численно.

Из условия (5) следует, что a =

т   2R

2 np R 2    3

Это, в частности, означает, что при фиксированных т , р и R параметры а и b являются зависимыми, то есть класс роторов конической формы может быть описан лишь одним параметром. Выберем для описания параметр b , а параметр а будем находить из соотношения связи (8).

Так как z (0) >  0 и z (R) >  0 , то должны выполняться два условия: а >  0 и а + bR >  0 , из которых с учетом (8) следует, что

"   = 2 np R 3 - ^b - ^{b max} = 4 np R 3 .

Поскольку полутолщина z однозначно задается одним параметром b , функционал момента импульса L зависит от двух вещественных параметров ш и b :

L(ш, b) = 4 прш / г ³ (а + br) dr = -mwR² +-- bпршR⁵ .

о              '        2            15

Задача (7) на классе конических роторов упрощается и принимает вид:

M(y) = max L(ш,b) , (ш,ь)екц где множество Ky задает область параметров, удовлетворяющих условию прочности:

K = {( ш , b) G [0, + то ) х [b mm ,b m«z ] : 6_ц ( ш ,Ь ) 6 [ а ]}.

Здесь S _y ( ш , b) — функция максимальных напряжений, определяемая выражением (4), в котором z(r) = а + br , параметр а находится из (8).

Значения ( ш ,Ь ) , обеспечивающие максимум (11), будем называть оптимальными для заданного µ . Ротор соответствующего профиля будем называть оптимальным в классе конических тел.

Мы будем пользоваться фактом, что функции L( ш , b) и S _y ( w , b) возрастают при фиксированном ш > 0 с возрастанием b . Для первой это следует из (10). Для второй функции это утверждение оставляем в качестве гипотезы, основанной на физических рассуждениях, что увеличение b соответствует перераспределению массы ближе к краю с одновременным уменьшением толщины в центре, что должно привести к увеличению максимального напряжения материала ротора. Гипотеза подтверждается численными экспериментами.

Приведем некоторые значения функции L( ш ,b) :

31  3

L ( ш ,b m^n ) = 10 т ш R² , L ( ш , 0) = ^ т ш R² , L (ш^ тах ) = 5т ш R² .

Пусть

^ p = {ш >  0 : {ш}х [b min ,b ma_Ж ] П K p = 0} ,   B p ( ш ) = { b G [b min , b m^ ] : ( ш ,Ь) G K p } .

Тогда max L(ш,b) = max max L(ш,b).

( ш ,Ь) Е К ^              ше п ^ Ь Е В ^ ( ш )

В силу установленной монотонности функции L ( ш , b) по b , внутренний максимум в правой части достигается на значении Ь ( ш ) = max В _р ( ш ) . Используя монотонность функции S _p ( ш , b) по b , мы можем численно находить Ь ( ш ) методом дихотомии. Из уравнений (1) и (2) следует факт монотонного возрастания функции S _p ( ш ,b) по ш . Поэтому функция Ь ( ш ) монотонно убывает. Это позволяет оптимизировать вычисления при построении области прочности.

Численное значение M ( p ) можно найти, например, следующим способом. Для значений параметра ш , начиная от нуля с шагом 5ш > 0 и пока В _р ( ш ) не пусто, находим значения L( ш ,b( ш )) , среди которых выбираем наибольшее.

Для проверки условия прочности применялся конечно-разностный подход. Краевая задача (1), (3) дискретизировалась в рамках конечно-разностного подхода следующим образом:

U = 0,

d i U ' - i + biUi + C i U i+i = f i ,

i = 1, n — 1,

П _п - П _п -1 h

+ p ^ =0.

Здесь n — заданная размерность приближенной задачи; h = R/n — шаг сетки; r = ih , u _i — аппроксимация для u(r _i ) , i = 0,n ; a _i = A ' /h² — B _i /(2h) ; b _i = — 2A _i /h 2 + C _i ; C i = A i /h ² + B i /(2h) ; f i = —рш ² г ² г(^ i )(1 — p ² )/E ; A ' = r ' z(r i ) ; B i = z ( t' ) + r i zfr f ) ; C i = p Z ‘ (T i ) — z(T i )/T i .

При этом конечно-разностные аппроксимации напряжений o _r (r _i ) и o _t (r i ) вычислялись по формулам

	O r,i =л ' 2 (bU i + p ),    O t,i =л ' 2 (pS U i +     ), i = 1,n   1, 1 — p \         ri)           1 — p \         ri) E O r,0 = O t,0 = 1    pb U 0 ,
где	S _ U1 — U o      S _ U i+1 — U i - 1    . _ 1---—J      S - U n — U n - 1 0         h ,           '           2h      ,     - ,        ,          n~        h      .

Функцию максимальных напряжений S _p ( ш , b) , определяющую область прочности (12), аппроксимируем следующим образом:

^S p ^{( ш} , ^{b )    max} {ff _r,0 , ..., G ..-, . ° t,0 , •••, ^O t,n ^} .

• 3.    Частные интегрируемые случаи конических роторов

В семействе конических роторов можно выделить два интегрируемых случая. Запишем решения для этих случаев и будем их использовать для тестирования сходимости численных решений. При b = 0 краевая задача (1), (3) имеет решение

—

Р^ш 2 ^{(1 —} p ^{2 )} _r 3 8E

pш2R2(3 + p)(1 — p) u(r) = -----------------------r v '              8E

При а = 0, что соответствует случаю b = bmax, краевая задача (1), (3) имеет решение рш2(1 - »2)(3 + »)Я3 s s   рш2(1 - »2) 3

^ ^й                  ^

(s + »)(11 + »)Е         (11 + »)Е где s = ний:

^5- ₂ ^4µ-1 . Из этого можем получить значения функции максимальных напряже-

S „(ш, 0) = ^{max {}^ ⁺ »’ ^ —^1 рш²К²,    S„ (ш,Ь_тах) = то .

»      ,                                                         ,             »      , /mUX

Замечание 1. Из последнего соотношения следует, что при любом » G ( - 1,1) для области прочности (12) выполнено включение:

К » С { 0 } ^{X [ b} min , ^b max ] и (0, + то ) ^{X [ Ь} тгп , ^b

max

).

Для диска равной толщины ( b = 0 ) максимальное ш , удовлетворяющее условию прочности (12), задается выражением:

ш _п ( » ) =

%]

р max { 3 + » ; 2 — 2 »}

Отсюда находим, что максимальный момент импульса M d ( л ) для диска равной толщины, при выполнении условия прочности, имеет следующий вид:

M d ( » ) =    ш ( Л ),0) = ' "  G   '" = _тД /        ^^]

2           у р max { 3 + » ; 2 — 2 »}

• 4.    Результаты расчетов4.1.    Результаты тестирования сходимости

Приведем результаты тестирования сходимости численного решения к точному в описанных выше интегрируемых случаях.

Таблица 1

Оценка погрешности численного метода при b = 0 , » = 0 , 3

n	10	100	10 3	10 4	10 5	10 6
max | п(Г г ) - n ^ | max | u(r ^ ) |	1, 46 • 10 — 1	1,48•10 — 2	1,48•10 — 3	1,48•10 - 4	1,48•10 - 5	1,46 • 10 - 6
max | n ‘ (r ^ ) —5 n ^ | max | n ‘ (r t ) |	9, 76 • 10 — 2	9,19•10 — 3	9,11•10 - 4	9,09•10 - 5	9,09•10 - 6	9, 27 • 10 - 7

Таблица 2

Оценка погрешности численного метода при b = b _max , » = 0 , 25

n	10	100	10 3	10 4	10 5	10 6
max | u(r i ) — u " |	1, 35 • 10 — 1	1,39 • 10 — 2	1, 74 • 10 — 3	5,63 • 10 — 4	1,78 • 10 — 4	5, 65 • 10 — 5
max | n(r i ) |

При других значениях ц Е ( — 1; 1) результаты аналогичны. Прослеживается сходимость порядка О(1/тг) для b = 0 и порядка O(1/ti ^s ) для b = b max . Для b = b_max сходимость более медленная, так как имеет место особенность первой производной точного решения в нуле.

• 4.2.    Область прочности

Пользуясь приведенным выше алгоритмом численного решения, рассчитаем область прочности (12) в зависимости от ц Е ( — 1,1) . Результаты расчетов приведем на рисунке 2. Серым цветом выделена область параметров ш и b , удовлетворяющих условию прочности при ц = 0, 3 . Показаны границы этой области при некоторых других значениях µ .

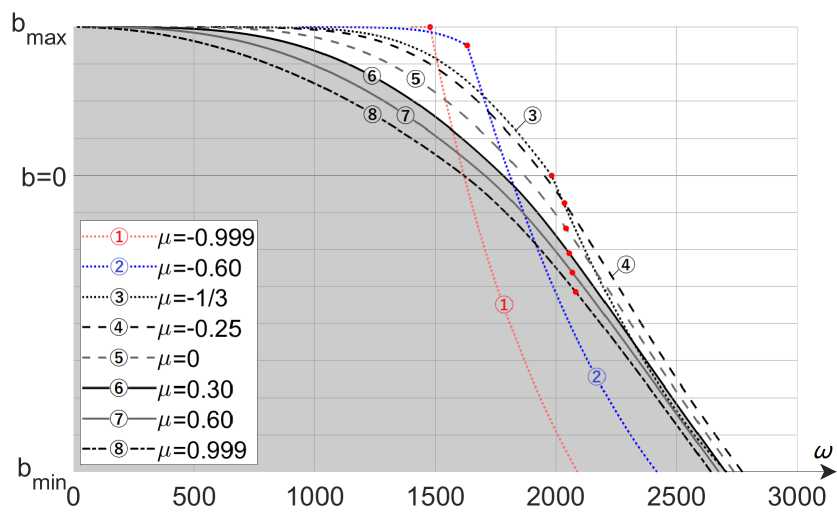
Рис. 2. Область прочности К ^ для некоторых значений ц

На рисунке 2 для каждого из указанных значений µ выделены точки максимума ( ш ( ц ), Ь ( ц )) функционала момента импульса (10) по области К _ц . Они перечислены ниже в таблице 3 вместе со значениями целевого функционала М ( ц ) = £ ( ш ( ц ) ,Ь ( ц )) и относительным выигрышем по сравнению с моментом импульса ротора постоянной толщины (14) при заданном µ .

Отметим, что с ростом ц от — 1 до приблизительно - 1/4 область прочности изменяется не монотонно. В частности, она «сокращается» при больших значениях b (около b_max ), но «растет» при меньших значениях b . Около значения ц to — 1/4 характер «немонотонности» усложняется и требует отдельного исследования. Начиная со значения ц to — 1/4 область прочности монотонно убывает с ростом ц .

Значения величин ω и M даны в единицах системы СИ: раcд и кг·см2 соответственно. Остальные величины являются безразмерными. Справочно приведем значения bmax = 0, 0354,     bmin = —0, 0708.

Таблица 3

Точки максимума момента импульса (10) по К ^ в зависимости от ц

µ	-0,999	-0,6	— 1/3	—0,25	0	0,3	0,6	0, 999
ω	1 477	1 632	1 981	2036	2 042	2 055	2 068	2 082
ь	0,0354	0,0311	0,0000	-0,0066	-0,0127	-0,0186	-0,0232	-0,0279
M	25,5266	27,6169	28,5335	28,2151	27,2980	26,4854	25,8755	25,2637
M - M n M n	9,5%	6,0%	0,0%	0,4%	1,5%	3,2%	5,4%	8,4%

4.3. Эффективность конических роторов

Эффективностью оптимального конического ротора при заданном ц G (—1,1) по сравнению с ротором постоянной толщины назовем отношение M^^^ максимального

момента импульса (11) к моменту импульса ротора постоянной толщины (14).

На следующем рисунке представлена зависимость эффективности оптимального конического ротора от ц G ( - 1,1) .

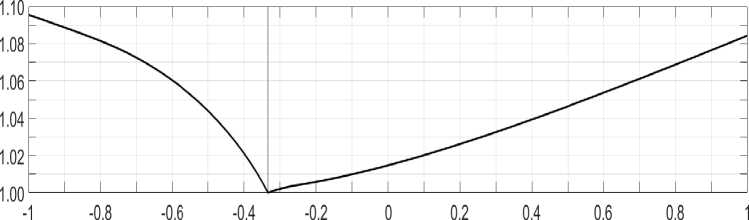
Рис. 3. Выигрыш эффективности оптимального конического ротора по сравнению с диском постоянной толщины

Из графика, приведенного на рисунке 3, видно, что при значениях µ , близких к ± 1 , прирост эффективности составляет порядка 9 % относительно диска постоянной ширины, а при значении ц = 0, 3 прирост эффективности составляет приблизительно 3,2 %.

На рисунке 4 показаны графики оптимальной угловой скорости ω оптимального конического ротора и максимальной угловой скорости ш _д диска постоянной толщины (13), выраженные в [род] в зависимости от ц G ( — 1,1) .

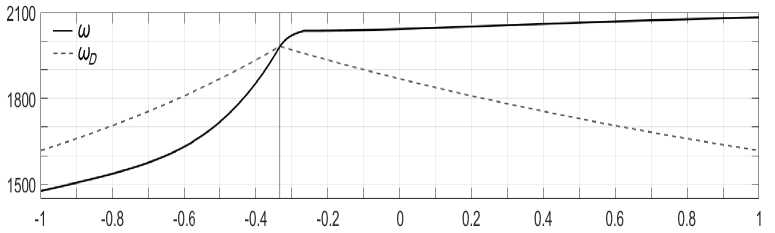
Рис. 4. Значение оптимальной угловой скорости ω и максимальной угловой скорости Ш п диска постоянной толщины в зависимости от ц

На рисунке 5 изображен график оптимального наклона профиля Ь , конического ротора (выраженного в безразмерных величинах) в зависимости от коэффициента Пуассона ц G ( — 1,1) .

Рис. 5. Значение оптимального наклона b в зависимости от ц

Из рисунка 5, в частности, следует, что при ц >  - 1/3 толщина оптимального ротора убывает от центра к краю ( Ь < 0 ), а при ц <  - 1/3 — наоборот ( Ь > 0 ).

На рисунках 3-5 отмечено значение ц = - 1/3 , для которого оптимальный ротор совпадает с ротором постоянной толщины.

• 4.4.    Оптимальная форма стального конического ротора

Приведем иллюстрацию профиля оптимального конического ротора для ц = 0,3 (сталь).

На рисунке 6 серым цветом представлен профиль оптимального конического ротора для ц = 0,3 . Для наглядности показаны границы профиля диска постоянной толщины (сплошная линия) и границы роторов для Ь = Ь_тщ и Ь = Ь_тах (прерывистые линии), имеющие ту же массу. Оси градуированы в сантиметрах. В целях читаемости данных масштаб по осям не сохранен.

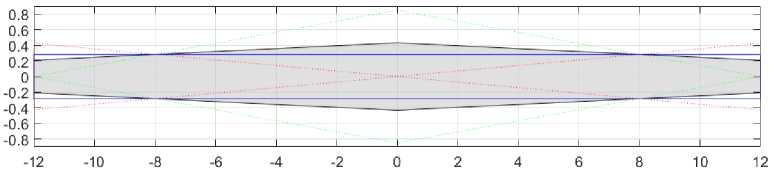
Рис. 6. Форма оптимального конического ротора при ц = 0 , 3

В таблице 4 приведены геометрические характеристики этого оптимального ротора в сравнении с диском равной толщины.

Таблица 4

Сравнение оптимального конического ротора с диском для ц = 0 , 3

Характеристика	Оптимальный конический ротор для ц = 0, 3	Диск равной толщины
Полутолщина в центре z(0), мм	4,32	2,83
Полутолщина на крае г(Я), мм	2,09	2,83
WO	2,068	1
Угловая скорость вращения, рад/с	2 055	1 781

Заключение

В статье предложен универсальный алгоритм, работающий для широкого набора параметров конструкции и характеристик материалов ( R,m, р ,Е, [ ст ], ц ), для нахождения оптимальной формы ротора гиродина в классе конических тел. В случае, рассматриваемом в работе, а именно, для стали при радиусе ротора R =12 см, преимущество в моменте импульса найденного конического ротора над ротором постоянной толщины составляет 3 %.

Подход к поиску оптимальной формы ротора, предложенный в работе, допускает обобщение / расширение на случай тел вращения более сложной формы, чем конические, но это сопряжено с увеличением вычислительных затрат.

Следует отметить несколько факторов, не учтенных в работе:

• •    Не рассмотрен способ крепления ротора гиродина к оси вращения и, соответственно, не оценено влияние этого способа крепления на характеристики ротора.

• •    При прецессии оси вращения ротора изменяется напряженно-деформированное состояние тела ротора и оно будет существенно отличаться от напряженно-деформированного состояния, которое исследовано в работе в рамках приближения «тонкого диска» с осесимметричным полем напряжений и деформаций.

Однако, если учитывать эти факторы, модель становится слишком сложной для эффективного поиска оптимальной формы.

Поставим ряд открытых вопросов и задач.

• 1)    Доказать монотонность функции S ( m ,b) по параметру Ь .

• 2)    Получить явную аналитическую оценку для ω max такую, что

  К ц С [0, ш

  
  

  max ] ^{X [ b} min , ^b max ^{] .}

  
  

• 3)    Исследовать более детально зависимость области прочности К _ц от параметра ц .

• 4)    Исследовать монотонность зависимости оптимальной угловой скорости ω от значения коэффициента Пуассона µ .

• 5)    Исследовать предельные случаи краевой задачи (1), (3) при ц ^ ± 1 .

• 6)    Рассмотреть случай профиля ротора произвольной формы.