Оптимальная нелинейная фильтрация оценок информационного воздействия в стохастической модели информационного противоборства

1. Введение. Постоянное расширение аудитории социальных сетей и мессенджеров обуславливает значительный рост их влияния на жизнь человека в обществе. Это стимулирует интерес ученых к исследованию процессов информационного воздействия социальных медиа на формирование общественного мнения [1–6]. Наличие у платформ социальных медиа открытого описания способов программного взаимодействия (API – application programming interface) при одновременном развитии сторонних библиотек и расширений (numpy, requests, pandas, seaborn, networkx и пр.) высокоуровневых языков (python), автоматизирующих рутинные функции обработки, визуализации и анализа данных [7], увеличивает мотивацию подобных исследований с позиции формализации представлений при применении, совершенствовании и разработке методов математического моделирования информационного противоборства и управления в структурированном социуме.

Методологическую основу формализованного исследования социальных медиа при построении математических моделей информационного противоборства и управления составляют теории вероятностей [5, 6, 8], игр [2], графов [2, 9] и дифференциальных уравнений [3, 4, 10]. Основные подходы математических представлений по получению оценок информационного воздействия базируются на анализе активных сетевых структур [3] и дифференциальных уравнений [2]. С позиции относительной простоты и точности модели анализа реальной социальной сети в условиях неоднозначности и неполноты информации атрибутивного пространства взаимодействующих пользователей первичной предпочтительностью обладает математическая формализация, основанная на представлениях систем дифференциальных уравнений – модели информационного противоборства в структурированном социуме [2, 4, 10]. Их математическую запись, обобщенно учитывающую выделенные в [2, 4, 10] факторы распространения информации в социуме, можно определить в следующем виде [11]:

k ' = У тк (t)

M amk(t) + ^^ вm′ m (t)xm′k (t) m‘ = 1

^Y mk (t^x mk ^(t);

dy mk ^(t) dt

dx mk ^(t)

dt

M

^Y mk (t^y mk ^{(t) +}

^{+ a} mk ^{(t) +} ^^ ^в m ^′ m (t) x m ^′ k (t)

L          m ‘ = 1

N m    X X ^(x mk ‘ ^{(t) +} y mk ’ ^(t))^ ,

где m' ,m e {1, M}; k = 1, K; K - число субъектов, в отношении которых в социуме формируются предпочтения у индивидов; M – число подгрупп, выделяемых в социуме; Nm – число индивидов в m-й подгруппе M при обозначении N0 = ^2 Nm общей численности социума; xmk и ymk – число адептов и пmре=д1адептов соответственно k-го субъекта из m-й подгруппы социума; αmk и γmk – интенсивности положительной и отрицательной информации, распространяемой внешними источниками в отношении k-го субъекта при учете особенности их восприятия индивидами m-й подгруппы; βm′m – интенсивность межличностной коммуникации индивидов т'-й и m-й подгрупп; t e [t0,t1] - момент времени ([t0, t1] - временной интервал анализа).

Отдельно следует уточнить, что в формируемом решении на основе математических приближений вида (1) не исключается возможность комбинации моделей информационного противоборства в структурированном социуме с активными сетевыми структурами, к примеру, применяемыми для оценки измеряемых параметров α mk , β mk , γ mk [12]. Недостаток моделей информационного противоборства в структурированном социуме [2, 4, 10] состоит в детерминированном определении их параметров ( α _mk , β _mk , γ _mk ), что не позволяет в полной мере оценить степень различия между исходными факторами ( x mk , y mk ) конкурирующих субъектов.

Для устранения указанного недостатка в работах [11, 13, 14] в развитие [2, 4, 10] предложено вводить флуктуацию в измеряемые параметры модели – интенсивности α _mk и γ _mk . При этом за методологическую основу составления стохастических математических моделей в [11, 13, 14] выбрана теория марковских процессов и процессов диффузионного типа [15, 16]. Для увеличения точности оценки x mk , y mk на фоне наблюдаемых α mk , γ mk , содержащих стохастические компоненты с параметрами отличными от нормального закона распределения [17], в [18] при введении дополнительного фиктивного стохастического дифференциального уравнения состояния разработана схема нелинейной фильтрации. Она предполагает сведение задачи анализа исходного стохастического дифференциального уравнения к численному решению уравнения Дункана–Мортенсена–Закаи [19] спектральным методом Галёркина [20].

Основной недостаток решения [18] заключается в фиктивном введении стохастического дифференциального уравнения состояния (составляется из исходного при оценке стохастических компонент наблюдаемых интенсивностей агитации методами полиспектрального анализа [21]) в формировании модели оптимальной нелинейной фильтрации оценок информационного воздействия.

Цель настоящей статьи состоит в устранении указанного недостатка [18] при разработке вычислительно эффективного решения обобщенной задачи оптимальной нелинейной фильтрации оценок информационного воздействия в стохастических моделях информационного противоборства. Для достижения сформулированной цели в развитие результатов [18] необходимо решить следующие задачи:

• 1)    формализовать постановку задачи оптимальной нелинейной фильтрации оценок информационного воздействия в стохастической модели информационного противоборства, не предполагающую введения фиктивного стохастического дифференциального уравнения состояния;

• 2)    в разрабатываемой задаче оптимальной нелинейной фильтрации при определении эволюции функции плотности вероятности уточнить особенности применения робастного уравнения Дункана–Мортенсена– Закаи [22];

• 3)    определить численную схему решения задачи оптимальной нелинейной фильтрации и при систематизированном представлении последовательности действий по получению оценок информационного воздействия в стохастической модели информационного противоборства, уточнении и конкретизации особенностей программной реализации составить соответствующий вычислительный алгоритм;

• 4)    выполнить сравнительное апостериорное исследование разработанного алгоритмического решения при выделении особенностей по устойчивости предложенной численной схемы и точности получаемых

• 2.    Постановка задачи оптимальной нелинейной фильтрации оценок информационного воздействия в стохастической модели информационного противоборства. Рассмотрим динамическую модель вида (1) для начальных условий x mk (t ₀ ) = y mk (t ₀ ) = 0, положив, что значения интенсивностей α mk , β m ′ m , γ mk зависят от t и складываются из истинных величин 0 <  a mk (t) , в т ‘ m (t), Y m _k (t) <  ^ и шумов наблюдения a mk (t), в т ’ т (t), Y mk (t) с соответствующими статистическими параметрами: E [a _mk ] = E [/3 _m‘_m] = E [Y mk ] = 0;

  cov ^[a mk , ^a m ‘ k ‘ ^]

  
  

оценок.

Для общности представлений стохастической модели информационного противоборства, в отличие от [18] установим зависимости от времени и наличие стохастической компоненты в интенсивности межличностной коммуникации β m ′ m .

dt · εαmkm′ k′ ; cov βm′m, βj′j m′ mj′j ;

cov [7 mk , 7 m ‘ k ‘ ] = dt • ^e mkm ‘ k ‘ (k,k e {!,K}; m,m ' ,j,j ' e {1,M}). Опираясь на представления [11, 13, 14, 18], запишем (1) в виде системы стохастических дифференциальных уравнений:

dZ = A (Z, A ⁰ , B ⁰ , Г 0 ,t J dt + S ( Z, t\

dW,

где ^A     (^a mk ) m _x k ; ^B     (^в т ‘ т ^ м xM ^{; Г}    (^Y m k ) M xK .

Способы определения элементов вектора переменных Z , вектора

⃗

⃗

сноса A , диффузионной матрицы Σ и вектора шума W , с учетом (1) и представлений [11, 13, 14, 18], уточнены в приложении.

Уравнение (2) устанавливает правило измерения численности адептов и предадептов в структурированном социуме при наблюдаемых интенсивностях α mk , β m ′ m , γ mk . Потенциально соответствующие параметры α _mk , β _m ′ _m , γ _mk возможно определять различными методами при обеспечении условия некоррелированности шумов наблюдения. Так, например, интенсивности α mk и γ mk распространения положительной и отрицательной информации о k -м кандидате в m -й подгруппе социума допустимо задавать отношением числа сообщений соответствующей тональности (положительная и отрицательная) к периоду времени наблюдения при учете их объема и вероятностных характеристик тональной оценки [18]. При этом соответствующая вероятностная оценка отдельного сообщения может получаться при применении различных алгоритмических решений. Они, например, программно-реализованы в таких библиотеках python как Dostoevsky, TextBlob, BERT, ruGPT-3 или представлены в виде самостоятельных программ [18, 23]. Их основу составляют алгоритмы машинного обучения и словарные методы [23]. Также и величина β m ′ m может определяться различными не взаимоувязанными способами. Частное решение по нахождению β m ′ m приведено в [24].

Указанное позволяет справедливо предположить о наличии второго независимого от первого правила наблюдения a mk , в т ‘ _т , Y'_mk соответствующих параметров интенсивностей α mk , β m ′ m , γ mk в модели (1) при неопределенности в предпочтительности первого и второго правил наблюдения. При этом аналогично α mk , β m ′ m , γ mk интенсивности ^a mk , m'_m‘ m , Y mk складываются из истинных величин ^a mk , ^e m ‘ m , Y m k и шумов наблюдения <5t'_mk (t) , mm'^m ‘ _m (t) , Y mk (t) с соответствующими статистическими параметрами: E [a mk ] = E [,3 m‘m| = E [Y mk ] = 0;

cov ^[a mk ^,a m ‘ k ‘ ^] = dt • ^r ^km ’ k ’ ; cov ^m ‘ m ^,e ‘j]

dt · ε

. в m′ mj′j ;

cov ^[Y mk , ^Y m ‘ k ‘ ^] = dt • ^mkm ’ k ’ • В этой связи, запишем вторую систему стохастических дифференциальных уравнений наблюдения за численностью адептов:

dZ ' = A Zz ' , A ⁰ , B ⁰ , r ⁰ ,t) dt + S ' Zz ' ,t) dV,          (3)

где элементы вектора переменных Z ^′ , вектора сноса A , диффузионной матрицы Σ ^′ и вектора шума V^⃗ , задаются аналогичным (2) способом (см. приложение) при учете правил определения α ^′ _mk , β _m ^′ ′ _m , γ _m ^′ _k .

Уточним, что уравнения (2), (3) будем понимать в смысле Ито [16].

Я

Задача фильтрации состоит в получении оценок Z = I Z l I числа адептов и предадептов k -го субъекта m -й подгруппы в момент времени t ∈

Я

[t ₀ , t 1 ] из заданных уравнений (2), (3). Оценку Z выполним по критерию максимального правдоподобия:

Z = arg max

Z^⃗ ∈ Ω

p Z, t

где p Z , t – апостериорная условная функция плотности вероятности распределения .Z е П.

Функцию p ^Z, t^ при p ^Z, t^ = ф ^Zi, t) j R ф ^Zi, t) dZ определим по теореме сложения вероятностей [26] из:

как вероятность суммы двух совместных событий, наступающих при составлении следующих двух пар уравнений состояния и наблюдения для формирования модели оптимальной нелинейной фильтрации: 1) уравнение (2) задается состоянием, а (3) – наблюдением; 2) уравнения состояния и наблюдения определяются в обратном порядке.

В этом случае, эволюцию апостериорных условных функций плотности распределения вероятностей p1 Z⃗, t , p2 Z⃗ , t из (5) при p1,2 (Z, t) = *1,2 (Z, t) ^f *1,2 (Z’t) d"Z и заданном начальном условии *1,2 ^Z, t0^ = p0 (zj определим из решения уравнений типа Дункана–Мортенсена–Закаи (ДМЗ) [18, 19]:

d* 1,2 (Z,t) = L 1,2 [^1,2 (Z,t)]dt+

+*1,2 (Z,t) [A2,1 (Z,t)]T [D(2,1)) (t)] 1 dZ2,1, где A (Z,t) = AyZ, A, B, Г,#); A2 (Z,t) = AyZ, A, B', r',t); A = (amk)MxK; B = (em‘m)MxM; Г = (Ymk)MxK; A = (amk)MxK; b' = (em‘т)мXM; Г' = (Ymk)mXK; D(1) = №)„ „ = ssT; d(2) = X     / dxd

(D(,A    = S'S'T; d/B2 1 - приращение вектора .Z, определяемое ll dxd уравнениями (3), (2) соответственно; L1,2 [^] - диффузионные операторы

Фоккера–Планка–Колмогорова [19]:

d Л               1 d dд2

L12 и =—X dZ [A-0] + 2 XX dZddZ- [D»-21*]- l=1 l                    l=11‘=1l l

Уточним, что в заданных в выражении (6) обозначениях для определения функции *1 используются операторы и функции с соответствующим первым индексом - L1, A2, D(2) и dZ2. Для нахождения *2 применяются компоненты из (6) с соответствующим вторым индексом. В последующих соотношениях будем придерживаться указанного правила.

Сформированные представления (4)–(6) формализуют исходную постановку задачи оптимальной нелинейной фильтрации оценок информационного воздействия в стохастической модели информационного противоборства при выполнении условий нормировки [13, 14]: R p(Z,t\dZ = 1; Rp 1,₂ (Z,t)dZ = 1;

Q                   Q

p(Z,t) >  0; P 1,2 (Z,t) >  0.

Следуя результатам [25, 27], для повышения точности численного решения задачи нелинейной фильтрации при снижении чувствительности фильтра к дискретному во времени изменению траектории наблюдения для

P i,2 ( Z, t o) = p₀ ZZ\ уравнение (6) представим в робастном виде [27]:

T

"t^T = - dt ( '^{T |} Ml ) Z ²,^{1 P 1},^{2 +}

+ exp {-A T ,i D        Z 2,i} [L i,2 - 2 4, 1 [ D^ ] ^- a4 2,1] x ⁽⁸⁾

X [exp {4,1 [D(2,1)] 1 Z2,1} P1,2] , при обозначении:

^ 1,2 = exp 1-Д ,1 [ d ^{(2 , 1)} ]   Z^A P 1,2 .

Для заданной постановки задачи (4), (5), (8), (9), учитывая результаты [11, 13, 14, 18, 25, 27], сформируем численную схему оптимальной нелинейной фильтрации оценок информационного воздействия в стохастической модели информационного противоборства.

• 3.    Численное решение задачи оптимальной нелинейной фильтрации оценок информационного воздействия в стохастической модели информационного противоборства. Наибольшую трудоемкость и основу в сформированной задаче фильтрации (4), (5), (8), (9) составляет решение уравнения (8). Его исследование выполним в постановке спектрального метода Галёркина [20] при дискретизации интервала наблюдения [t ₀ , t ₁ ] на тактовые подынтервалы t G [т _п , т _{п +1} ] (At = т „₊1 - т „ ; n = 0, N - 1; N = (t 1 - t o )/ At) [28]. Следуя утверждению 1 [25] (утверждение 2.1 [27]), для заданной дискретизации t G [т _п , T n+₁ ] в формируемом численном решении сведем задачу (8), (9) к рекуррентному решению последовательности подзадач, составляющих основу Yau-Yau’s алгоритма [25]:

^1,2 ( Z, Тп-1) = ^1,21 (Z,T„-1) X где при Ф1 2 ( Z, то ) = Ф1 2 ( Z, to ) = Р0 (Z I значения ф 1 2 ( Z, тп-1 определяются из решения прямого уравнения Колмогорова [25]:

^ФГ- ¹ (z,t) = l 1,2 [фп, - ¹ (z,t) ]

T                  ¹

- 2Ф П,-¹ (z, t) [>12,1 (Z, t)\ [d ^{(2 , 1))} (t )J     >1 2,1 (z, t) .

Учитывая результаты [13, 14, 18], решение прямого уравнения Колмогорова (11) выполним численно при введении следующих представлений.

U

S w ^(u) набором из U симплексов u=1

= 1 ) Л ( V i = 1,d + 1, Z (^u) >  0B C

Зададим разбиение П =

/ , C ^{d+ 1}      \   1 X ( d l z ,

^ ^(u) = j P z iu p iu : P z iu I i=1             \i=1

R d (u =1,U) с d + 1 вершинами P ₁ ^(u) , P ₂ ^(u) ,..., P d+)1 и барицентрическими координатами Z ^(u) ,..., Z d+)₁ при ^{ш (и)} ^ ^{ш (и} ) = 0 (u = u ‘ ; u, U E {1, U}).

Обозначим (• , •) □ скалярное произведение:

⟨ η, ϕ ⟩

ηZϕZ

- 2^ dZ,

для некоторых функций η и ϕ.

Зададим аппроксимацию <^П,₂ ^Z, t^ ненормированных функций

Ф П,2

плотности вероятности:

U

Ф П2 (Z,t) = ЕЕ c !j²⁾ (t) j (Z), u=1 j e J d

подстановка которых в (11) в проекционном представлении метода Галёркина сведет исходную к системе обыкновенных дифференциальных уравнений:

G⃗

de ⁽¹,2) (t) = S ^{- 1} ( l ⁽¹ , ²⁾ (t) - Q ⁽¹,²⁾ (t)) 6 ⁽¹,²⁾ (t);

dt                                                          (14)

C ⁽¹,²⁾ (0) = S ^{- 1} G.

В выражениях (13), (14) приняты следующие обозначения:

vec ( G ) при G

П /(u)\

К№*j /J

; vec ( • ) - операция U X| j d |

векторизации матрицы; C ^(1,2) = vec ( C ^(1,2) ) - вектор искомых

коэффициентов разложения, зависящих от t, при C ^(1,2)    =

(c (1^>2))       ; l ⁽¹ , ²⁾ =           £ 1,2 [vO )       ; Q ⁽¹,²⁾ =

\ uj Zu x| J d |                    \\ ⁵       , I ⁵ J/Q/ U rX U r

(/ i (u) Л*Г Гтл(2 D) Л/Л1 ^—1 л i (u‘) \ A           c*      (/ i (u) i (u‘) \ A

* ^j ’,A_2a [D⁽ • " t А,# '’ U r x U r ; ^S = (. ^* ^j ',* 5' )„) _{U r} U r = U |J d |; u,u' E {1,U}; J d - множество мультииндексов j,j' E J d [13,14]:

J r^d

| j = ^(j 1 , .

. . , j i , .

. . , j d+1) ^{: j} i ^E Z + ,

X.   1

ji = r , i=1        )

где r E N - порядок аппроксимации на w ^(u) ; Z + = N U { 0 } ; * j^u) -базисная функция частичной подобласти w ^(u) E fi, которую зададим произведением:

d+1

*ju) = П фji i=1

Гауссовых базисных функций [29]:

Ф j i = exp

J - [2j i + 1 - 2Z i (r + 1)] ² [       2(d +1)

I

Принимая во внимание заданную дискретизацию временного интервала анализа и выбранную рекуррентную схему (10) оценки 754 Информатика и автоматизация. 2023. Том 22 № 4. ISSN 2713-3192 (печ.)

ISSN 2713-3206 (онлайн)

^ 1,2 , решение обыкновенного дифференциального уравнения (14) для соблюдения компромисса между точностью, вычислительной устойчивостью и сложностью выполним методом Эйлера [30]:

С (1,2) — С ⁽¹,²⁾ I { Q-1 Г(_Т ⁽¹,²⁾ _ П⁽¹,²⁾ Х Г ⁽¹,²⁾ 1Х Л S')

C n = C n - 1 ⁺ ^t "^S    ^L n - 1 Q n - 1 J C n - 1 J J,     ⁽¹⁸⁾

где C n^1,2) = C ⁽¹-²⁾ (T n ); L„ ^,2) = L ⁽¹,²⁾ (r n ); Q^ ,²) = Q ⁽¹,²⁾ (T n ).

(1,2)

Вычисленные выражением (17) коэффициенты C n , с учетом (10) и аппроксимации (13), нормируются по правилу:

С (i,²) ₌ c (1,²) /( c ^(1,2) С^ n nn / l^n    ^ j ,

а затем уточняются соотношением:

(5 n¹’²) = S ^{- 1} [Q n^ C n1,²⁾] ,                   (20)

где Q ^{, (1,2)} = (D^ ju) , exp {A T ,1 [ D ^(2,1) ]

• ¹    dZ 2 ,A ^ ^(u)) ) при ) ^j /л/ U r X U r

Q n(^1,2) = Q ^{, (1,2)} (r _n ) и рассчитываемых элементов ^A 2,1

~

в момент времени r _n ; Ф

Ф uj = R ^ j^u) (Z) dZ .

vec

при Ф =

, D ⁽²,1) , dZ 2,1 uj ) u x J d | для

w ( u )

Определение искомой функции плотности вероятностей p Z^⃗ , t в момент времени τ n осуществляется при ее аналогичной (13)

U                 (u)

аппроксимации -p Z?,t) = P P c uj (t) ^j- (Z), где коэффициенты

• ^{4    2} u=1 jeir               ^{v 2}

c uj для (C = vec ( C ) и C = (c uj ) U _x| j d | задаются при дополнительной нормировки (19) полученных (5 nn^1,2) из (20) по правилу:

Cn = c n¹) + c n²⁾ - S ^{- 1} C n ; C n = C n/ (с _п ф) ,      (21)

⃗ где Cn = С (Tn); Cn =

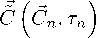
для C n

vec I C n I при C n =

((^n^,^ ^(u)\ )

V\         j /nU и x| j d|

.

Поиск максимума

(4) осуществляется методом Ньютона [31] ^

для начального приближения Z ⁰ , выбираемого с учетом следующего

a U выражения: Z0 = P P CujФ^и), где Ф^и) = JM(u) Z^(u \^z\dLZ.

u=i jeJr                                      ^{v 7}

В целом, перечисленные правила вычисления эволюции функции ^

Z , τ n и оценки Z составляют суть численного решения задачи оптимальной нелинейной фильтрации

оценок информационного воздействия в стохастической модели информационного противоборства. Исследование вопросов существования, единственности и сходимости сформированного численного решения при неизменности операторных представлений в (11) и выбранной системы базисных функций согласуется с результатами [13, 14, 18]. Задание элементов векторов и матриц в (18), (20) обеспечивается численным вычислением интегралов вида (12) с применением кубатурных формул [14] для симплексов [32]. Также для минимизации вычислительных затрат при расчете матриц S, Q^1,2), Cn из (18), (20), (21) соответственно учитывается их симметричность, а нахождение элементов матриц S, Cn реализуется аналитически через функции ошибок (используются результаты, полученные при доказательстве лемм из [13]). Последнее определяет дополнительную предпочтительность применения в качестве аппроксимирующих полиномов Гауссовых базисных функций (16) в сравнении с другими U видами специальных функций [33]. Алгоритм разбиения fi = S w(u) u=1

набором из U симплексов при формировании триангуляции [34] уточнен в [14]. Эффективный алгоритм формирования множества мультииндексов (15) приведен в [35].

Для систематизированного представления последовательности ^

действий получения Z по составленному численному решению, приведем алгоритм оптимальной нелинейной фильтрации оценок информационного воздействия в стохастической модели информационного противоборства. При формировании алгоритма используем результаты [13, 14, 18, 36].

• 4.    Алгоритм оптимальной нелинейной фильтрации оценок информационного воздействия в стохастической модели информационного противоборства. Входными данными

  алгоритма являются: 1) временной интервал анализа [t ₀ , t i ]; 2) число отсчетов дискретизации N; 3) число K субъектов, в отношении которых формируются предпочтения у индивидов; 4) количество M подгрупп в социуме; 5) численность индивидов N m в m-х подгруппах U

  социума; 6) порядок аппроксимации г; 7) разбиение fi = S w ^(u) ;

  u=1

  8) наблюдаемые матричные функции интенсивностей A , B , Г и А ’ , В ’ , Г ' ; 9) начальное распределение функции плотности вероятности

  
  

  ^p

  
  

  = P o

  
  

  -1 exp

  σ 0

  
  

  Z T S _o Z I , где ^ ₀ - нормирующий

  
  

  множитель, обеспечивающий выполнение условия R p ₀ (Z) dZ = 1;

  Q ' ²

  
  

  ^s o = (=?,‘) d , d .

  
  

  Выделим основные этапы работы алгоритма, полагая неизвестными а          в          Y            / а          'в         ' Y

  параметры ε _mkm ′ _k ′ , ε _m ′ _mj ′ _j , ε _mkm ′ _k ′ , ε _mkm ′ _k ′ , ε _m ′ _mj ′ _j , ε _mkm ′ _k ′ .

  Шаг 1. Методом полиспектрального анализа [18, 21] в

  
  

  отношении функций a mk , в т ’ т , Y mk , a' _mk , e m ‘ m , Y m к выполнить оценку соответствующих величин интенсивностей Ck, e m ‘ m , ^ mk , ^a ' mk , ^e ' m ‘ m , у mk и усреднением ^a mk = о, 5 ^m k +, C ‘ m = ⁰, ⁵ (3 m ‘ m ⁺ Z m’m) , Y m k = ⁰, ⁵ (i m k ^{+ Y} 'm,k) определить приближения для соответствующих истинных значений интенсивностей.

  
  

  Шаг 2. По средневыборочным правилам [35] для α mk , β m ′ m , Y mk , ^ mk , ^e m ‘ m , Y mk и найденных Q mk , ^e m ‘ m , Y m k определить оценку соответствующих параметров ε ^α _mkm ′ _k ′ , ε ^β _m ′ _mj ′ _j , ε ^γ _mkm ′ _k ′ , ε _m ^α _km ′ _k ′ , ε _m ^β ′ _mj ′ _j , ^ mn,_km ‘ _k ‘ для задания ковариационных матриц шума D ^(1,2) .

  Шаг 3. Положить n = 0 и установить начальные значения ZZ n = 0, z n^i,2) = 0, Z n = 0.

  Шаг 4. При заданной p ₀ ZZ^ определить (D _n = C7 n^1,2) = S ¹ Gv.

  Шаг 5. Для момента времени τ n вычислить ковариационные

  
  

  (1,2) матрицы D n

  
  

  .

  
  

  Шаг 6. По методу Эйлера (Эйлера–Маруямы [37]) выполнить экстраполяцию 2?П+1 с учетом моделей (2), (3):

  
  

  у ⁽¹⁾ _ у ⁽¹⁾

  Z n+1 = Z n

  
  

  + At.A (^ П¹) , А , В , Г , T n ) ;

  
  

  7 ⁽²⁾    7 ⁽²⁾ I AfZ (7 ⁽²⁾ a' r' T' -t ) Z n+1 — Z n ⁺ ^^tA I Z n , A , B , 1 , ^T n ) .

  
  

Шаг 7. Учитывая представления (14), (18), для τ _n рассчитать _т (1,2) ,^(1,2) матрицы L n , Q n .

Шаг 8. Если n > 0, то:

• a)    принимая во внимание (20), рассчитать:

  C n^i,2) = S

  
  
  
  
  
  

  [ Q    ■.,

  
  

где Qn(1’2) = Q'(1 ’2) (тп), пои О'(1,2) - f/^(u) хо//т G'(2Д)0        ^            G'(1’2) - при Q — \j3 , exP |A2,1Gn j Tj' /         для Gn    —

Г_п(1,2) 1 ^{- 1} f G (1,2) _ G (1,2) \

[D n J    ^Z n       Z n - 1 J;

• б)    нормировать полученные векторы С n^1,2) по правилу (19).

(1,2)

Шаг 9. С учетом выражения (18), вычислить С пЗ 1 с последующей нормировкой результата соотношением (19).

Шаг 10. С учетом выражения (21), рассчитать (3 _{п +1} .

Шаг 11. Для найденного (5 _{п +1} по правилу (4) методом Ньютона [31]

Д определить оценку Z n₊₁ .

Шаг 12. Увеличить n — n + 1 и проверить условия:

• а)    если n < N , то перейти к шагу 5;

• б)    если n — N , то завершить работу алгоритма и вывести результат Д Д Д

вычисления - Z ₀ , Z 1 ,..., Z N - 1 .

Псевдокод сформированного алгоритма оптимальной нелинейной фильтрации оценок информационного воздействия в стохастической модели информационного противоборства, с учетом указанной общей последовательности действий, приведен в виде листинга 1 – функция FilterRatings .

Вспомогательные функции в приведенном листенге 1 реализуют следующие вычислительные процедуры:

• 1)    Polyspect Estim – определение приближения для соответствующих истинных значений интенсивностей a ^k , в т ‘ m , Y m k (шаг 1 алгоритма);

function F lLTER R ATINGS (t o ,t i ,N, K, M N i_____ N _M Д ,p o ,

A , B , Г , A ‘ , B ‘ , Г ‘ ){

( A ⁰ , B 0 , Г 0 ) = P OLYSPECT E STIM ( A , B , r , A ‘ , B ‘ , r ‘ );

( e ^a , 6 ^е , 6 ^Y , 6 ‘^a , 6 ‘^e , 6 ‘^Y ) =

C ALC V ARIANCES ( A ⁰ , B 0 , r ⁰ , A , B , r , A ‘ , B ‘ , Г ‘ ); n = 0;

( 1,2 )

Z n = 0; 2 П    = 0; Z n = 0;

• △ t — ( t i ^- t o )/ ( N ^— 1 ) ; ^T n — t o ;

S — 1 •-"',-'" .-V. ,.: G P ^Л’

( 1,2 )

C n — C ALC SLAE( S ,G); C n — N ORM V ECTOR (C n ); С П — C n ;

while (n < N) {

D n ¹ ) — D IFFUSION E STIM ( e ^a , e ^e , e ^Y ДП^ );

о П ²⁾ — D IFFUSION E STIM ( e '^a , e '^e , e '^Y , Z n2 ) );

Z n + 1 — Z n1 ) + △ t A ( Z n ⁱ⁾ , A , B , Г , T n ) ;

Z n + 1 — z n ²⁾ + A tA^ n ² ) , A ' , B ' , r ' ,T n ) ;

L n ⁱ²⁾ — L ⁽¹²⁾ ( A 12 , D n ¹²⁾ ,T n ) ;

Q n ^{1 2} — Q ⁽¹ , ²⁾ ( A ,1 , о П ^2,1) ,T n ) ;

if (n > 0) {

G n ^(1,2) — [ D n ^i,2) ] ^-1 ( Z n ^i,2)

z ^(1,2)v ^Z n - 1 ) ;

Q n ⁽ 1, ²⁾ — Q '⁽¹ , ²⁾ ( A 2,1 , G n ^(1,2) ,T n ) ;

( 1 2 )         _' ( _{1 2} ) ( 1 2 )

^C n — ^Qn ^C n ;

C n1 ^,2) — C ALC SLAE ( S , C n1 ^,2) ) ;

Cn1,2) — NORM VECTOR(Cn1,2));} dC(1,2) — (Ln12) - Qn1,2))Cn1,2);

dC ^(1,2) — C ALC SLAE ( S , dC ^(1,2) ) ;

(1,2)        (1,2)(

Cn+1 — Cn   +AtdC

(1,2)(

C n ₊ 1 — N ORM V ECTOR ( C n ₊ 1 ) ;

^        ^_z z ( 1,2 )

^T n + 1    ^T n ^{+ A t ; C} n + 1    ^{C ( C} n + 1 ^,T n + 1 ) >

C n + 1 — C ALC SLAE ( S , C п + 1 ) ;

• ( 1 )          ( 2 )

C n + 1 — N ORM V ECTOR ( C n + 1 + C n + 1 - C n + 1 ) ;

Zn+1 — ARGUMENTMAXIMUM(Cn+1); n — n + 1;} return (Zo,.

.

. ^{, Z} N - 1 )^}

Листинг 1. Оптимальная нелинейная фильтрация оценок информационного воздействия в стохастической модели информационного противоборства

• 2)    Calc Variances – средневыборочная оценка параметров ε ^α _{mkm k} ′ , ε ^β _{m mj} ′ _j , ε ^γ _{mkm k} ′ , ε ^′ _m ^α _{km k} ′ , ε ^′ _m ^β ′ _mj ′ _j , ε ^′ _m ^γ _{km k} ′ (шаг 2 алгоритма);

• 3)    NormVector – нормировка (19);

• 4)    DiffusionEstim - вычисление ковариационных матриц D ⁽,^L2) (шаг 5 алгоритма), с учетом правил задания матриц Σ , Σ ^′ , уточненных в

приложении;

• 5)    Argument Maximum – максимально правдоподобная оценка Д

Z n+1 в соответствии с правилом (4) при численном нахождении оптимума методом Ньютона [31] (шаг 11 алгоритма);

• 6)    Calc SLAE – решение системы линейных алгебраических уравнений [38].

• 5.    Результаты вычислительного эксперимента. Для апостериорного исследования предпочтительности полученных результатов проведем серию вычислительных экспериментов при решении задачи моделирования и оценивания стохастической модели информационного противоборства вида (2), (3) для K = 2, M = 1 (малые значения K , M выбраны из соображений наглядности демонстрации графических результатов вычислительных экспериментов). При проведении указанных испытаний особое внимание уделим результативности сформированного алгоритма (листинг 1) при вторичном уточнении его устойчивости и вычислительной сложности. Выделенные свойства алгоритма при изменяемом уровне нестационарного негауссовского шума в наблюдаемых интенсивностях моделей (2), (3) апостериорно установим при сравнении данных моделирования

Д точного решения X0 = (xk)K, Y0 = (y0)K с оцениваемыми: 1) Z по

Д средневыборочным правилам Z = ( Z + Z‘ I /2 результатов наблюдений

Д/

Z^⃗ , Z^{⃗ ′} из моделей (2), (3) соответственно; 2) Z^{⃗ ′} из моделей (2), (3)

Д/ ансамблевым расширенным фильтром Калмана [39]; 3) Z′ алгоритмом фильтрации, основу в котором составляет численное решение уравнения ДМЗ (6).

В качестве истинной модели информационного противоборства при проведении вычислительных экспериментов произвольно выбрана следующая система обыкновенных дифференциальных уравнений:

dy 0 = dt

X N o

Y k (xk - y 0 ) + (a k + x) - P (x k ‘ + y 0 ‘ ) - y o l;

k ^′ =1

X

dx ⁰ _k dt

y0 [ak + e0xk] - Yoxk; xk = 0; y0 = 0; k = [1; 2], где a0 (t) = 0, 25 |1 + 2cos (15t)|; a^ (t) = 0, 25 |1 + 2sin (5t)|; в0 (t) = 0,005 |2 + 5cos(0,1t)|; yO (t) = 0,05 |sin(20t)|; y0 (t) = 0,1 |cos(2t)|.

Решение (23) при определении эволюции -X 0 = (x k ) K , Y 0 = y _k ⁰ _K осуществляется числено методом Эйлера для аналогичных (22) N , At.

При обеспечении условия формирования в компонентах αk , β, γk и α′k , β′ , γk′ нестационарного негауссовского шума для моделей (2) и (3) соответствующие наблюдаемые интенсивности заданы следующими правилами:

• 1)    a k (t) = | a 0 (t) -N (0,q i ) | , в (t) = | в ⁰ (t) —N (0, q i ) | , Y k (t) = ^| Y 0 (t) —N (0,q i ), где N (0, q i ) - функция генерации случайных чисел, подчиняющихся нормальному закону распределения со средним 0 и дисперсией q 1 ;

• 2)    a k (t) = |a k (t2 + R ( q - 1 / 2)|, в ’ (t) = |в ⁰ (t) + R ( q-¹ / 2)|, Y k (t) = ^| Y 0 (t) + R ( q ₂ 1 / 2)^|, где R ( q - 1 / 2) - функция генерации случайных чисел, подчиняющихся экспоненциальному закону распределения со значением показателя экспоненты равным (2q 2 ) ^{- 1} .

Другие входные данные алгоритма заданы следующими величинами: t ₀ = 0; t 1 =4; N = 480; N ₀ = 10; r = 33; q 1 = 0, 5; q 2 = 0, 25.

Для компактности представлений результаты вычислительных экспериментов приведем в отношении значения суммы адептов и предадептов k-го кандидата ^k (t) = xk (t) + yk (t).

На рисунке 1 представлены графики зависимости от времени элементов векторов численности адептов: 1) истинного ^w                                                                                                ^w

~

~.

ξ _k ⁰ ; 2) определяемого среднего ξ k из моделей (2), (3); 3) оцениваемого ξ _k ^′ ансамблевым расширенным фильтром Калмана [39]; 4) оцениваемого l,'_k по алгоритму фильтрации, предполагающему численное исследование уравнения ДМЗ (6); 5) оцениваемого ξ k по разработанному алгоритму, основанному на численном исследовании робастного уравнения ДМЗ (8).

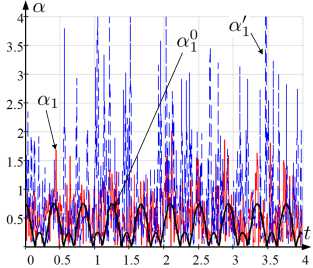
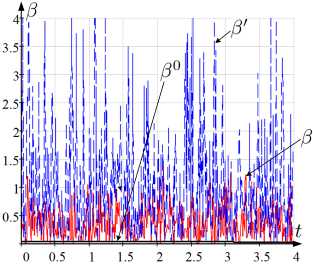
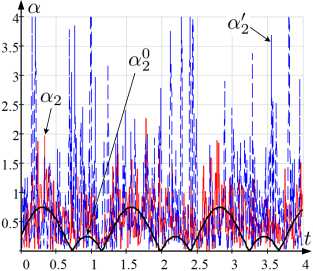
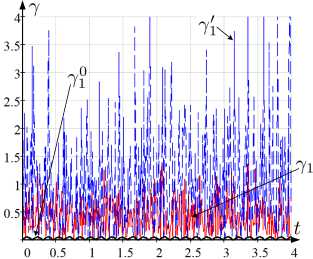
На рисунке 2 отражены графики наблюдаемых и истинных значений интенсивностей a k , в, Y k , a k , в ’ , Y k и a k , в ⁰ , Y 0 для t G [t o , t i ], используемых при оценивании ξ _k ⁰ , ξ _k , ξ _k ^′ , ξ _k ^′ , ξ _k (рисунок 1).

На рисунке 3 приведены графики одномерного среза апостериорных условных функций плотности вероятности p Z^⃗ , t , p 1 Z^⃗ , t , p 2 Z^⃗ , t в различные моменты времени t G [t ₀ ,t 1 ]. Ориентация плоскости среза выбиралась по максимальному значению дисперсии относительно ^ оцениваемого по правилу (4) значению Z.

Количественно сравнительную предпочтительность получаемых результатов ξ k , ξ _k ^′ , ξ _k ^′ , ξ k по отношению к ξ _k ⁰ установим величиной накопленной средней квадратической ошибки,

˜

значение которой, например, для ξ k определено по правилу

I    N - 1 K I             2 I

△ ё = 1/N E E l € 0 (t n ) - ^ k (t n ) |

У n=0 k=1

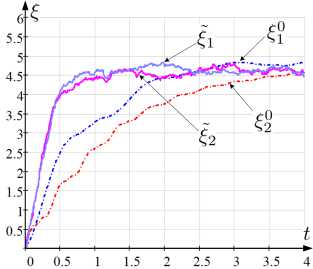
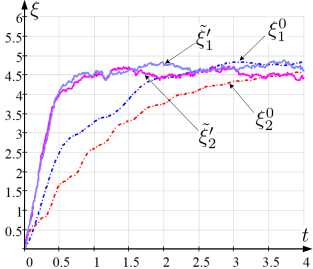
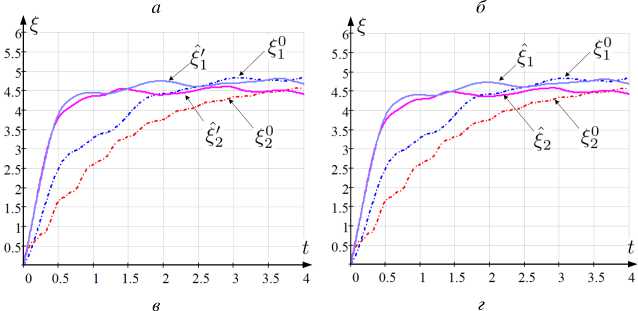
Рис. 1. Графики зависимости от t : а) ξ k⁰ , ξ k ; б) ξ k⁰ , ξ k^′ ; в) ξ k⁰ , ξ k^′ ; г) ξ k⁰ , ξ k

Также сопоставление результатов выполним при определении отклонения расчетного от истинного значения для заключительного момента времени K I                                      I наблюдения: 5^ = ^ |$0(tN-1) — £k(tN-1 )| [40]. Для проведенного расчета (рисунок 1) при q1 = 0, 5, q2 = 0, 25 значения А и 5 составили: △ё = 1,11; А^’ = 1,076; А^ = 0,988; А^ = 0,945; 5^ = 0,366; д^ = 0, 275; §!‘ = 0, 231; 5^ = 0, 208.

а

в

б

г

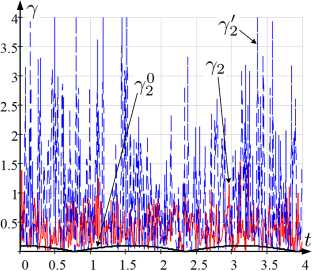
Рис. 2. Графики зависимости от t а) α 1 , α ^′ ₁ , α ⁰ ₁ ; б) α 2 , α ^′ ₂ , α ⁰ ₂ ; в) β , β ^′ , β ⁰ ; г) γ 1 , γ 1 ^′ , γ 1 ⁰ ; д) γ 2 , γ 2 ^′ , γ 2 ⁰

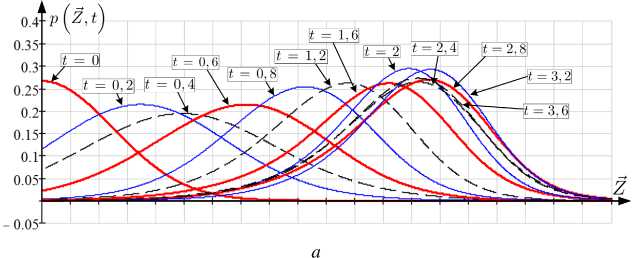
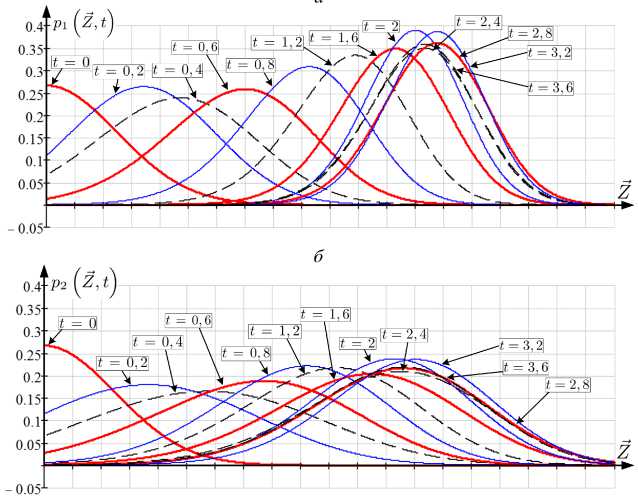
Рис. 3. Графики срезов для разных t : а) p Z^⃗ , t ; б) p 1 Z^⃗ , t ; в) p 2 Z^⃗ , t

Полученные частные результаты (рисунок 1) свидетельствуют о том, что сформированный алгоритм обеспечивает более точную оценку в сравнении с известными решениями [11, 13, 14, 39]. При этом интерес вызывает исследование соотнесенного выигрыша при изменении q 1 , q 2 .

Очевидно, что при росте ошибок в наблюдениях α k , β, γ k , α ^′ _k , β ^′ , γ _k ^′ вычислительная устойчивость составленного численного решения будет 764 Информатика и автоматизация. 2023. Том 22 № 4. ISSN 2713-3192 (печ.)

ISSN 2713-3206 (онлайн)

снижаться. Для ее повышения при сохранении адекватности нахождения функций p Z⃗, t , p1 Z⃗ , t , p2 Z⃗ , t требуется увеличить число точек дискретизации N на выбранном интервале наблюдения [t0 ,t1 ] (рисунок 4).

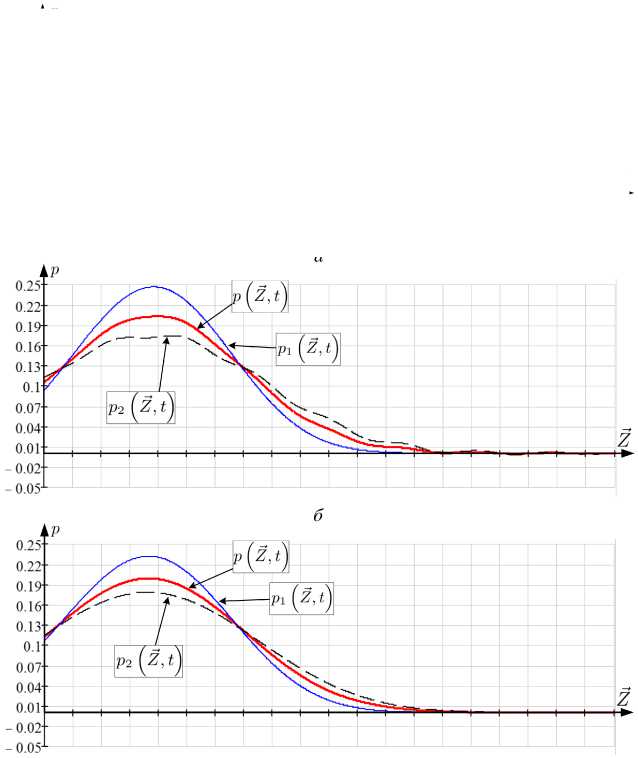
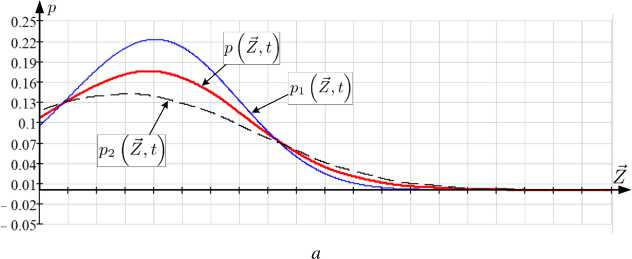
в

Рис. 4. Графики срезов p , p 1 , p 2 для t = 0 , 2 , q 1 = 0 , 75 ; q 2 = 0 , 5 q 1 , полученных при численном исследовании: а) уравнения ДМЗ при N = 480 ; б) робастного уравнения ДМЗ при N = 480 ; в) робастного уравнения ДМЗ при N = 500

Графическая иллюстрация отмеченной особенности приведена на рисунке 4 при представлении одномерного среза апостериорных условных функций плотности вероятности p Z^t t), p1 Z^t t), p2 Z^ t), рассчитанных при решении задачи фильтрации при применении уравнения ДМЗ (6) и робастного уравнения ДМЗ (8) (сформированный алгоритм) для t = 0, 2; q1 = 0, 75; q2 = 0, 5q1; N = 480 и N = 500. Из представленного примера (рисунок 4) следует, что на участках быстрого изменения числа адептов и предадептов (t е [0; 0,4], рисунок 1) при увеличении q1, q2 для недостаточного числа N при численном нахождении p (Z, t^, p1 (Z, t^, p2 (Z, t) наблюдается неравномерная (рисунок 4,б) сходимость выбранной аппроксимации вида (13). При этом в отношении применения робастного уравнения ДМЗ (8) в сравнении с простым уравнением ДМЗ (6) эта неравномерность проявляется более выраженно. Принимая во внимание указанное, выполнено сравнительное исследование точности сформированного решения при изменении q1, q2.

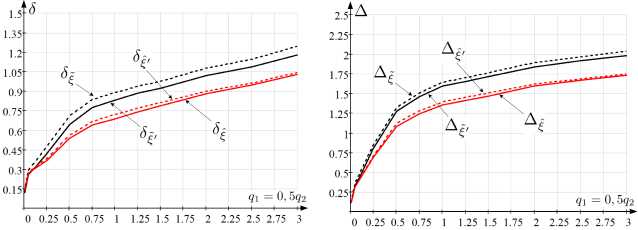
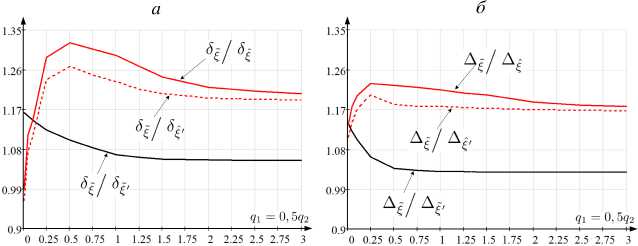
На рисунке 5 представлены графики зависимости усредненных по 10 ⁶ вычислительным экспериментам Д ^ , Д ^^ ’ , Д ^- ’ , Д ^- , 5 ^ , 5 ^ ’ , § 1 ‘ , 5 - от q 1 , q ₂ при q 1 = 0,5q ₂ (указанная зависимость выбрана из соображений соизмеримости уровня шума в соответствующих наблюдаемых интенсивностях моделей (2) и (3)).

• 6.    Заключение. Результаты проведенных вычислительных экспериментов (рисунки 1–5) подтверждают работоспособность разработанного алгоритмического решения оптимальной нелинейной фильтрации оценок информационного воздействия в стохастической модели информационного противоборства. Относительный выигрыш в сравнении со значениями, получаемыми по средневыборочным правилам наблюдения, в среднем равняется 20,7 % (рисунок 5). При этом аналогичный выигрыш применения ансамблевого расширенного фильтра Калмана составляет 7,4 %, а алгоритма нелинейной фильтрации, формируемого на основе исследования уравнения ДМЗ (6), – 17,3 %.

  

• 7.    Приложение. В (2) приняты следующие обозначения: Z Е П

  при Z = (Z l ) d = (z ⁽¹⁾ , z (²⁾ ,..., z (M) ) определяется численностью (m)\

  адептов и предадептов относительно m-и подгруппы Am) = |^zk J = ^(x m1 , y m1 , x m2 , y m2 , • • • , x mK , y mK ) [18]; ^П ^ ^ ^{X Y} ^X . . . X e ^(M) c R d — d-мерный (d = 2MK) выпуклый многогранник (правила параметризации П определены в [13, 14]); e ^(m) С R ^2K - симплекс с 2K + 1 вершинами [14]; A = (A l ) d = ( a ⁽¹⁾ , a ⁽²⁾ ,..., a ^(M) ) - вектор a (m) ₌ (_п^{( m )} \   ₌ ( fA f⁽²⁾ fA fA fA  fA ^

  сноса при a       ^^a k j 2K ^f m1 , ^f m1 , ^f m2 , ^f m2 , ^{. . .} , ^f mK , ^f mK J

  
  

  (2) для f mk =

  
  

  K

  N m    У? ^(x mk ‘ + y mk ’ ) y mk

  k ‘ = 1

  
  

  ^Y m k ^(x mk   y mk ) ^и f mk

  
  

  M

  y mk ^a mk ⁺ P ^e m ‘ m x m ‘ k

  m ‘ = 1

  
  

  M

  ^armk ⁺ P ^e m ‘ m x mk ⁺

  m ‘ = 1

  
  
  
  

  ^Y m k x mk ^;

  
  

  W = (W l ) _d = (w ⁽¹⁾ , w ⁽²⁾ ,..., w ^{( M} ) ) для w ^(m) = (w km) ^     =

  ( R⁽¹⁾ R)^ rA rA rA rA^ ^                  R⁽¹⁾ R⁽²⁾

  B m1 , B m1 , B m2 , B m2 , ^{. . .} , B mK , B mK J при ^{определении} B mk , B mk стандартными винеровскими процессами; S = (S ll ‘ ) _{d x d} = S ^a + S ^e +

  
  

вг

Рис. 5. Графики зависимости от q i , q 2 при q i = 0 , 5 q 2 : а, в) 5 ^ 5 ^ , 5 | ‘ , 5 | ; б, г) А ^ , А 1 ‘ , А ! ‘ , А ।

С позиции вычислительных затрат ансамблевый расширенный фильтр Калмана обладает преимуществом в сравнении со сформированным алгоритмом и способен при программной реализации на типовой ПрЭВМ обеспечить вычисления в режиме, близкому к реальному времени. По вычислительной устойчивости, определяемой равномерностью (рисунок 4(б)) сходимости выбранной аппроксимации функций плотностей вероятностей при одинаковой длительности интервала дискретизации ∆t, алгоритм, который основан на исследовании уравнения ДМЗ (6), обладает преимуществом в сравнении с разработанным алгоритмом (предполагает применение робастного уравнения ДМЗ (8)). Вместе с тем, по вычислительной сложности указанные алгоритмы сопоставимы и разработанный алгоритм обеспечивает наибольшую точность оценки. Таким образом, исходя из апостериорно определенного выигрыша по результативности решения (точноть оценки) при потенциальной возможности адаптивной вариации ∆t в зависимости от скорости изменения числа адептов и предадептов Z и уровня шума q1, q2 наблюдений а, в, Y, разработанное алгоритмическое решение обладает наибольшей предпочтительностью. Однако его применение в сравнении с ансамблевым расширенным фильтром Калмана становится нецелесообразным (рисунок 5) при малых значениях q1, q2 (снижение относительного выигрыша обуславливается вычислительной погрешностью в формируемых численных решениях по кусочно-полиномиальной аппроксимации и интегрированию).

В целом, полученные результаты в развитие работ [11, 13, 14, 18], формируют вычислительно эффективные решения обобщенной задачи оптимальной нелинейной фильтрации оценок информационного воздействия в стохастических моделях информационного противоборства при выделении особенностей основных этапов алгоритмической реализации. Составленный алгоритм применим при наличии неопределенности и разнородности правил измерения соответствующих интенсивностей α, β, γ модели (1). При наличии более двух разнородных правил подобного наблюдения, сформированный алгоритм может быть обобщен, при учете основных теорем теории вероятностей [26] и модификации правила определения итоговой функции плотности распределения вероятности (5). К направлениям дальнейших исследований относится получение априорной оценки, определяющей правило адаптивного выбора At в составленной численной схеме.

Σγ – матрица диффузии при:

^ a,e,Y _—

α,β,γ

°11

σ

α,β,γ

M 1

α,β,γ

. " 1M

α,β,γ σ MM

α,β,γ σ _mm ′

α,β,γ u 11mm'

α,β,γ

° K1mm ‘

. . ⃗σKα,Kβ,mm′

..s aKmYm ’

α,β,γ σ kk ^′ mm ^′

σα,β,γ σmkm′ k′ ga,e^Y

σ mkm ^′ k ^′

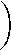
mkm ^′ k ^′

x mk V ^E mkm ‘ k ‘ ; ^

α mkm′ k′

αα ymk y^mkm’k’; umkm‘k‘

(TY ,       ,

σ mkm ^′ k ^′

β

σ mkm ^′ k ^′

Nm

K

P (xmk’’ + ymk’’)  ymk P^\ k‘‘ = 1                                 J

α mkm'k';

γ     β          ^MM β

— ⁽x mk y mk ) V ^e _mk_m ‘ k ‘ ; ° mkm ‘ k ‘ = ymk-I P P ^E j ^, mim ^l x j ’ k ;

У j=1 j ‘ = 1

Nm

K

У? (xmk’’ + ymk’’ k‘‘ = 1

) y mk

MM

εjβ′mjm j=1 j'=1

′ x j ^′ k .