Оптимальная по порядку оценка приближенного решения одной граничной обратной задачи для уравнения теплопроводности с переменным коэффициентом

Уравнение теплопроводности с учетом затрат тепла на термохимическое разложение теплозащитных покрытий гиперзвуковых летательных аппаратов, для конструкций которых во многих случаях применима одномерная модель, в приближении постоянства теплопроводности Л (хотя при точных расчетах необходимо учитывать изменения теплофизических характеристик при термохимическом разложении [1, 2]), записывается в виде ди     д ² и I др           X

— = а^г~й + ^ ;т, где а = — --температуропроводность, р, С„ - плотность и теп-dt     дхг   Срр dt          рСр лоемкость материала, I - тепловой эффект реакций термохимического разложения.

Актуальным является восстанавливать затраты тепла на термохимическое разложение во внутренних слоях, например, по результатам измерений температуры в неразлагающейся части теплозащитного покрытия в период до начала уноса материала с поверхности. С этой

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ целью можно принять модель: скорость изменения плотности во втором слагаемом в правой части уравнения теплопроводности пропорциональна температуре.

Новизна данной работы, по сравнению с [3], состоит в том, что граничные условия предполагаются оба ненулевыми, и снимается условие неположительности переменного коэффициента в уравнении теплопроводности.

1. Постановка задачи

Рассмотрим дифференциальное уравнение du(x,t)    д2u(x,t)      , . ,.

4т2 =   4’ + a(x)u(x,t),(1)

dtdx в котором x G [0,1], t> 0 и a(x) G С2[0,1]. Пусть известны следующие начальные и граничные условия:

u(x, 0) = 0, x G [0,1],

u(0,t) = f(t), t> 0,

u(xo,t) = g(t); 0 < x0 < I, t> 0, а граничное значение u(1,t) функции u(x,t) подлежит определению.

Задача (1) - (4) является некорректно поставленной, поскольку, как будет показано далее, изометричное интегральное преобразование сводит ее к задаче вычисления значений неограниченного оператора.

Предположим, что при исходных данных f (t)   = fo(t) G ^[0, от) и g(t) = go(t) G ^2[0, от) существует точное решение uo(1,t)^0 поставленной задачи, которое принадлежит пространству W^[0, от), причем для этого решения uo(1,0) = 0 и существует положительное число Т такое, что при t > Т uo(1,t) = 0.                                                (5)

Соотношение (5) является естественным, ибо всякий процесс имеет начало и когда-то прекращается. В данном случае , процесс изменения температуры прекращается в момент времени Т .

Кроме того, u o (1,t) G М _г , где

M _r = |u o G ^ 2^: [0, от ): ||u o||_wi <г}.                            (6)

Однако точные значения fo (t) и go (t) нам неизвестны, а вместо них даны некоторые приближения f^(t),gg(t) G L2[0, от) и уровень погрешности 6 >0 такие, что llfo -fs!l2<5,   |go -gsHl2<5.                              (7)

Требуется, используя исходные данные f^, g$, б, и М_г задачи (1) - (4), построить приближенное решение u§ (t) и оценить его уклонение ||u o — u§ ||l₂ от точного решения u o (t) = u o (1,t).

Согласно [3], наложенные на решение задачи (1) - (4) естественные условия и соотношение (5), позволяют использовать для нахождения ее решения интегральное преобразование Фурье по t G (—00, +от) в предположении, что u(x,t) = 0 при t < 0.                                  (8)

2. Сведение к задаче Коши

Учитывая (8), в качестве рабочего пространства Н возьмем гильбертово пространство, представляющее собой комплексный вариант L ^(— оо, + го ) над полем действительных чисел, его элементы и норма в нем стандартны, а преобразование Фурье на нем определим формулой

F [ ^u ( ⁱ )l ⁼ \^~ / и(Уе~^гтУ, т£ R.

В силу теоремы Планшереля, сформулированной, например, в [4] введенное преобразование изометрично.

Применяя к уравнению (1), с учетом условия (8), преобразование F , получаем

d2u(x, У , , х

-----h а(х)и(х,т) = гии(х,т); tR R, 0 <х< 1, dx²

где и (х,т) = F [ u ( x,t )l.

Для уравнения (9) поставим задачу, добавив условия

и (0,т)= /(г), rR R,

(Ю)

u(x ₀, у = д(т),    rR R,

^г д ^е 7 У) = ^{F [ f (} t )] , ^дУ = ^{F [} дУ)].

Из (9)-(11) требуется определить и(уУ = иУ, r R R .

Общее решение уравнения (9) запишем в виде:

и(х, У = с₁(т)е₁(х, У + сУУеУх, У,                       (12)

где е₁(х, У и е₂{х, У - линейно независимые непрерывные частные решения (9) Используя (10) - (12), получаем:

с1У) \ сУУ )

¹  ( ^е 2 ^(х о, У/У) - ^е2 ⁽0, У^дУ

^Е(У I -^е 1 ^(хо, yf⁽у + ^еУ⁰,у^д(у

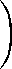
где Е У) =

^е 1 ⁽⁰У )

е 1 (хо, У

е2(0,У е 2 (х о, У

. При этом определитель Е (У считаем отличным от нуля

для всех т R R в силу линейной независимости рассматриваемых частных решений.

Тогда решение поставленной задачи можно записать в виде:

идо = ЕУ fX) + ЕУ gtR               (1 ³ )

Е У    Е У

где Е 1У) =

^е 1 ⁽¹>^х)

^е 2 ⁽¹Т⁾

^е 1 ^(хо>^т) _Ер м- ^е 1 ⁽⁰’^{т) е} 1 ⁽¹>^т)

е 2 (х о, У       ²          е 2 (0,т) е 2 (1,т)

3. Первое частное решение

Рассмотрим интегральное уравнение

X е1У у = е^ »^ - 1 о^ х'^ ( а(УеУ, УУ, J    R о У о

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ где /го = ^^^(1 + г), жД е [0,1], tR R.

Нетрудно убедиться, что если уравнение (14) имеет решение, то оно также будет являться решением уравнения (9).

Теорема 1. Существуют числа То > 0, c i > 0, С 2 > 0 , такие, что для всех \r\ > То выполняется двусторонняя оценка

х

.

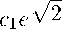
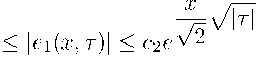
Кроме того, при \r\ >  Tq, \т\ ^ ж справедливо равенство

\ ^е!Д,т⁾ \ = у/ДД ^2      ^{(1 +} о ⁽¹ )).

Доказательство. к виду

Выполним замену еДж, т) =

1 _еЦ оСёх

еДж,т ) , тогда уравнение (14) придет

X оДт(х Де°0^

лД, Д = ¹ - / ------ z- ---аДДДДтМ.              ⁽¹ 7 ⁾

J    и оут e/w™

о

Обозначим c = max \а(х)\ . х е [о , 1]

Далее, для любого ау shp оДт (х — ()ед 0

" 0       0^/г 0Z Стх

>   0 найдется то

< ai.

>   0 такое, что для всех

Обозначим q i =

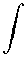
sh/j, ₀Дт ( х — Де^ ⁰^

Ц ₀Дт 0 Z

1 ^а (€)\Д • Тогда в силу полученных оценок бу

дем иметь: qi < aic. Поскольку оу - любое, то, в частности, можно взять оу = —, тогда 2c qi < 2, а соответствующее значение то нетрудно подобрать, зная ai.

Покажем, что при \т| >  tq решение уравнения (17) можно искать в виде

м

Е1Д,т) = ^Ещ (Х,Т), и =0

где

X

shp оДт ^(х — ^е^{0 0}^

,           "^^'^

о

Применяя индукцию по ц, можно показать, что Дщ (х, т)\ < qi , где ц = 0,1, 2,... м

Поскольку q <  1 , то ряд ^ец Д, т) равномерно и абсолютно сходится при х е [0,1] , и =0

Д| Д То и его сумма еДж, т) равномерно ограничена при \т\ ^ ж. Тогда имеем оценку:

1- q

1 - q i

.

1 - q i

Выполняя обратную замену и используя (18), находим:

х

,

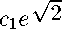
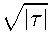
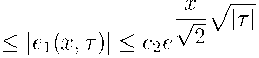
_ 1-2^ 1     _    ¹

^{ГДе C1} “2(1 -qi ) ’ ^C2 “2(1-_ft) •

Продифференцируем (14) ио переменной ж :

еКд, т) = ^^    -ph 1^ (ж - МОе^, тЖ

о и,

Тогда, используя доказанное выше, получаем, что

ММ, Ml < у/Не

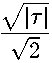
ж

следовательно, \е'₁(х,т)\ < \/\т\е

С другой стороны:

MifoMI >

УЯ _ж

/ ² (1 + о(1)) при \т\

^ № •

X

|м oVt ф«^|_ у oh/лоу/т (

о

ж

1 _ CC2

ж — Ма(Ме1ММ^

² (1 + о(1)),    \т\ ^ X .

(1 + ^C

\ Ум

Таким образом при \т\ ^ то справедливо равенство (16).

• 4.    Второе частное решение

Рассмотрим интегральное уравнение е2(Ж)Т) = е-[ *У/^М <)е2(е,МС

J      /Ж 0V^T

X где 0о = /| (1 + 2), ж G [0,1], тЕ R, £ G ^ж, /2j • Кроме того, будем считать, что при ж Е [1, \/2] а(ж) = а(1), т.е. а(ж) непрерывна на отрезке [0, V2] • Тогда для всех ж G [0, л/2] будет по-прежнему справедлива оценка \а(ж)| < с.

Снова нетрудно убедиться, что если уравнение (19) имеет решение, то оно также будет являться решением уравнения (9).

Теорема 2. Существуют числа tq > 0, C3 > 0, C4 > 0 , такие, что для всех \т\ > То выполняется двусторонняя оценка

ж

C3e

Д2

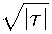
< Iе2М, т)| < C4e

ж /2

УЙЙ

Кроме того, при \т| >  Tq , \т\ ^ то справедливо равенство

1е2У,М| = УНе

УЯ

^/2      (1 + ₀(1)).

Доказательство. Аналогично теореме 1.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

• 5.    Следствия

Далее будем принимать за то > 0 то значение \т\ , начиная с которого выполняются оценки из обеих теорем.

Следствие 1. При С 2 = 2,С 4 = 2 и \т| >  то найдутся постоянные C 5 ,C g ,C 7 ,C 8 такие, что справедливы двусторонние оценки

С 5        >

С 7 У(е

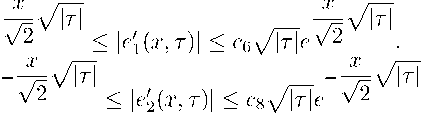
Следствие 2. При \т\ > то и С 1 С 7 = С 4 С 6 функции е 1(ж,т) и е 2(ж,т) линейно независимы, а значит образуют фундаментальную систему решений уравнения (9).

Заметим, что выполнения условия С 1 С 7 = С 4 С 6 всегда можно добиться в силу произвольности выбора констант q 1 и q 2 в теоремах 1 и 2.

Следствие 3. При \r\ >Tq и С 1 С 3 = С 2 С 4 справедлива оценка

1 - 2х о

С э е

V2

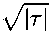
ЕКМ Е (т)

1 - 2х о

< Сюе

V2

УЙ

Доказательство. Из равенств для Е 1 (т) и Е (г) , используя известные неравенства для модуля суммы и разности, находим:

\\^е 1 ⁽¹,^х)\\^е 2 ^(хо, ^х)| - 1^е 1 ^(хо,т⁾\\^е 2 ⁽¹,т⁾\\ <  ^{Е 1 (т)} < JM12j1 lh ( * 0^r )l±l ^e^^

\ е 1 (0,т) \\ е 2 (хо,т) \ ± \ еД®о, т) \\ е 2 (0,т) \ ^_ Е(т) ^_ \\ е 1 (0,т) \\ е 2 (хо, т)| - |еД®о, т) \\ е 2 (0,т) \\ '

Используя результаты теорем 1 и 2, сосчитаем отдельно верхнюю и нижнюю оценки:

1 -Хо

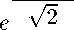
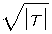
2хо - 2

С 2 С 4 ± С 2 е

^2

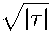
\ ^e 1 ( ¹,T^)||e 2 ^(x0, Т⁾ \ ± \ ^е 1 ^(хо, Т⁾ \\ ^е 2 ⁽¹,Т⁾ \ \\ ^е 1 ⁽⁰,Т⁾ \\ ^е 2 ⁽ ® о, Т⁾| - |^е 1 ⁽ Ж о, Т⁾ \\ ^е 2 ⁽⁰,Т⁾ \\

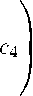
е М2      С ₁ С ₃ е ^{Х о} Мй — с ₂ с ₄

1 - Хо

е

-Й2

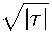
2хо - 2

С 1 С 3 - С 2 е

Й2

Уйй

С 4

llle(1,2j1Ih<Хoд^^

\ ^е 1 ⁽⁰,Т⁾ \\ ^е 2 ^(хо, т) | ± \ ^е 1 ^(хо, Т⁾ \\ ^е 2 ⁽⁰,Т⁾ \

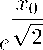
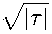
с ₂ с ₄ е ^^ ^i ± с ₂ с ₄

Таким образом, поскольку \т| > то >  0 , то справедлива оценка

1 - 2х о

С э е

Й2

Е^т) Е (т)

1 - 2х о

< С1о е

^2

УН

где С э =

\ С 1 С 3 - С 2 С 4 \       =      2С 2 С 4

2С 2 С 4      ^,           \ C 2 C 4- С 1 С з \ .

Следствие 4. При \т\ >Tq и С 1 С 3 = С 2 С 4 справедлива оценка

1 ~хо с9е

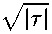
Е 2 (т)

Е (г)

1 - Ж о

< С1о е

х'1

vVi

Доказательство. Аналогично предыдущему следствию.                            □

• 6.    Метод проекционной регуляризации

В силу изометричности рассматриваемого преобразования Фурье и в силу (7) получаем, ^что 11/0- Тб \\l₂<$, И з о -95 ||l₂<^-

_Л ч Е 1 (т) _Л . Е2(тД.

Обозначим U1(t) = ——ту/ (т) и U2(t) = ——туз(т), тогда задача (12) примет вид:

Е И)             Е И)

U (1,t) = U (t) = U i (t) + U 2 (t) .

При |т| < т_о получаем, что И и (г) - и ₀ (г)|| <  дД с ₁₁ + с ₁₂ , где с ₁₁ = max т е[-то,то]

Е 2 (т)

С1 2 = max  —— .

¹² те[-то,то ] Е (Д

При |т| > То запишем задачи для функций U 1 и и ₂ в операторной форме:

Е(Т Е (т)

,

Е(Т                     Е(Т

А1и1(Т) = ЕДд)и1(т) = Т5^^ А2и2(П = ЕДД и2(т) = 95 ДД где А1, А2 : Н ^ Н.

Следствие 5. Операторы А 1¹ и А 2 ¹ , определяемые формулами (25), неограничены.

Пусть и ₁о (т) ,и ₂о (т) G ^2(“ °°, +^ю ) ^_ точные решения задач (25), соответствующие правым частям / о (т) и 9 о (т) соответственно. Тогда, в силу принадлежности точного решения и о (1 ,£ ) классу корректности (6) и соотношения (8), найдутся постоянные Г 1 ,г₂ >  0 такие, ^что ll^U 10 ^И L ₂ + ^ИU ^0 ^И L ₂<  ^{г 2 , ИU} 20 ^И L ₂ + ^ИU 20 ^И L ₂ <^Г 2 ^{и Г} 1 + ^г 2 = Г . + ^

Определим июД ) = у — У и1о(Де~^гт*дд. Тогда и ' _1о (т) = iииоДт).

Значит, для точных решений ищ и и 2о справедливы неравенства:

(¹ + М²) ||^U10 ^И L ₂ <^{г2 ,}    (¹ + И²) ll^U20 ^И L ₂ <^г2                     ⁽²⁶⁾

Из следствий 3 и 4 вытекает инъективность операторов А 1 , А * , А 2 и 4 2 , поэтому в силу леммы 6, сформулированной в работе [5], существуют изометрические операторы Q 1 ,Q 2 : Н ^ Н такие, что A 1 U 1 (t) = Q 1 C 1 U 1 (t) и A 2 U 2 (t) = Q 2 C 2 U 2 (t) , где

C 1 U 1 (t) =

Е (Д ЕДТ

U 1 (t) ,

C 2 U 2 (t) =

Е (Д Е 2 (т)

ДД) ,

то есть операторы С 1 и С 2 положительно определены и самосопряжены. Таким образом, уравнения (25) могут быть приведены к виду

С 1 ^и 1 ⁽т⁾ = Т /г/ С 2 ^и 2 ⁽т) = иИ,

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ в котором fg(т) = Q*f§(т), 'gg(т) = Q^dSф), а Q1 и Q2 операторы, сопряженные соответ-

Р А           ^Е ^ ^|Е 1 ⁽^

^Е И 1 Е (г) | Е2(т) I E (t)I '

и Q ₂ =

с ^тв енн ^о с ^Q i = —-— ^Е 1Ф ⁾ I ^{е (}г⁾|

Из (26) и (27) следует, что, при f оФ ) = Q 1 / o(t)_ и g _Q (r)_= Q 2 g o (r) уравнения (28) имеют точные решения ищф ) G BS _{r i} и п ₂о (т) G BS _{Г 2} , где S _{r i} = [v : v G H, ||7|| < г₁}, S _{Г 2} = {v : v G H, Щ <  Г 2}, It\ >  T₀, а

Bv(t) = —^=^=v(r),

M > To, тф) G H.

Из формул (27) - (29) следует, что B = G i (C i ) и B = G ₂ ( C ₂ ) , где функции G ₁(cr) и G ₂ (a) являются строго возрастающими, непрерывными, удовлетворяющими условиям G i (0) = О и G ₂ (0) = 0 (см. [5]).

Используя следствия 3, 4 и формулы (27), (29), нетрудно показать, что имеют место эквивалентности:

G i (a)     ^{(1   2Ж о ) 2} In- ²         ,   G .  -             '^   ' In- ²              - - 0.           (30)

2          \ ^ /                  2          уст /

Используя метод проекционной регуляризации, предложенный в [5], регуляризуем ис-

ходные данные задач (28) (f( (т),5) и (д( (т), 5), то есть определим gg Ф1 «2 (5)] следующим образом:

функции fg [т, 31 (5)] и

- при условии ||/(51| >  35 определим fg [т, «1(5)] = <  ^{fd (т) при}

I 0 при

И < адд

Н > 31 (5)

, где «1 (5)

удовлетворяет уравнению невязки

- S1(<5)

-ОО                    31 (<5)

• -    при условии I f^H < 35 определим fg [т, «1 (5)] = 0.

и                                I д^ Ф) при |т| <а₂ф)

• -    при условии 1д₅ || >  35 определим д₅ [т, «2(5)] =   0 при |т| >  Л₂ф)

—02(6)               fw

, где «20 )

удовлетворяет уравнению невязки

-ОС                    02 (<5)

- при условии Цд^Ц < 35 определим g_s [т, а₂(5)] = 0.

При выполнении этих условий функции fg [т, 31 (5)] и gg [т, 32 (5)] определяются однозначно даже в случае неединственности решения уравнений невязки.

Согласно методу проекционной регуляризации операторы С /¹ и С /¹ , определенные формулами (27), применительно к функциям fg [т, 31 (5)] и gg [т, 32 (5)] уже являются ограниченными, а потому приближенные решения uig (щ) и U2d (т) уравнений (28) можно находить по формулам:

U 15 (т) = C 1 ¹ fg [т, 31 (5)], U26 (т) = С 2 ¹ д₍₅ [т, «2(5)].

В силу оценки из работы [5] и доказанных выше эквивалентностей (30), найдутся постоянные С 1з и С 14 такие, что при т >70 справедливы оценки

||« 1<5 - U 1o|| < С13 In ²

1\

5/

lUg — U 20II <  С 14 In ²

1\

5/

Постоянные С13 и С14 определяются оценкой из работы [5] и соотношениями (30) следу ющим образом:

С 13 = 126 1 —— 2^ ° )  = 66 1 (1 - 2® о ) ² , С 14 = 126 2 ⁽¹  2^ ° ^  ⁼ 66 2 (1 - ^ж о ) ² где

6 1 >  Г 1Ц ВЦ >1 и 6 2 >  ^ 2|| ^|| >  1.

1                                  П           , Г2

Находим ||В Ц = —^=^=, тогда выбираем 6 1 > —       >1 и 6 2 > —.      > 1.

V¹+ O'O                         V¹+ O'O             V¹+ O'O

Из теоремы, сформулированной в работе [5] следует, что оценки (31) являются опти мальными по порядку на классах BSri и BSГ2 соответственно, а соответствующие методы проекционной регуляризации оптимальны по порядку на этих классах решений.

Очевидно, что при |т| > т° справедлива оптимальная по порядку на классе BS _г оценка

Ци§ -и °|| < ( С 13 + С 14 )1п ²

где S _r = {v : v е Н, Ц и\\ < г} .

При т е R получаем, что Ц щ — и ° Ц²<  5² ( сп + с ₁₂ ) + ( с ₁₃ + с ₁₄ ) ² 1п^{- 4} I - ).

\о /

Чтобы окончательно получить приближенное решение щ(t) исходной задачи (1)-(4), применим обратное к F преобразование F 1[й(т)|

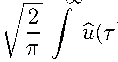
FTtdr,

е R и получим

^US (t) = R ^e {F ¹ [щ(т)| }. Поскольку преобразование F изометрично, то для приближенного решения щ ( t ) для любого I е R справедлива оценка:

1\

V

Ц щ - и ° Ц ²<  5²(с_п + С 12 ) + (С 13 + С 14 ) ² 1п ⁴

Далее остается отбросить все значения при t <  0 . Таким образом, справедлива

Теорема 3. Метод проекционной регуляризации для решения граничной обратной задачи (1) - (4) оптимален по порядку на классе BS_r.

• 7.    Выводы

Полученная оценка погрешности построенного приближенного решения напрямую зависит от точки i ° , в которой производится промежуточный замер температуры. С практической точки зрения это вполне объяснимо, ибо чем дальше от расчетной области производится промежуточный замер, тем менее точные результаты восстановления искомого температурного поля следует ожидать.

Также отметим, что реализация на практике описанного алгоритма может быть затруднительной, так как при численном моделировании необходимо решать интегральные уравнения (14) и (19) при всех значениях параметров, что может наложить дополнительные погрешности. Основная ценность полученной теоретической оценки состоит в том, что про нее известна оптимальность по порядку, потому, сравнивая с ней оценки других, более легко реализуемых численных методов (например, метода квазиобращения, рассмотренного в [6]), можно будет делать выводы об оптимальности по порядку именно их и реализовывать конкретно эти методы.

Работа проводилась при финансовой поддержке гранта р_урал_а (проект М 10-0196000).

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ