Оптимальное и квазиоптимальное отождествление объектов при структурно-системном мониторинге обстановки

Для повышения достоверности и полноты анализа обстановки в условиях априорной неопределенности и малой контрастности контролируемых объектов [1] используются методы структурно-системного мониторинга с совместной обработкой данных (сведений), добываемых разнородными средствами. За счет комплексного анализа демаскирующих признаков целей парируются их пропуски в отдельных каналах поиска (наблюдения), в том числе обусловленные мерами маскировки и снижения заметности [1; 2].

При структурно-системном мониторинге обстановки требуется выполнять отождествление данных (сведений), поступающих от независимых источников. Суть указанной процедуры заключается в установлении идентичности результатов поиска (наблюдения) в различных каналах путем сопоставления однотипных параметров и принятии решения о принадлежности признаков идентификации одному и тому же объекту [3; 4].

В предлагаемой работе на основе критерия минимума среднего риска [3; 4], обеспечивающего высокую надежность принимаемых решений при малом числе признаков идентификации [3], построены оптимальный и квазиоптимальный алгоритмы, найдены статистические показатели эффективности отождествления объектов [4] при наличии пропусков в сопоставляемых мас- сивах и использовании оценок максимального правдоподобия однотипных параметров [5].

Цель работы – исследование оптимального и квазиоптимального отождествления объектов при структурно-системном мониторинге обстановки.

1. Оптимальный алгоритм отождествления объектов с оценкой максимального правдоподобия однотипных параметров

Будем полагать, что отождествление выполняется между I объектами, выявленными первым средством мониторинга, с массивом признаков идентификации ^^(in)] в n-мерном пространстве, i = 1... I, n > 1, и J объектами с набором однотип- ных параметров

, j = 1... J, n > 1, зафикси- рованных вторым средством. Значения

и

^с j 7J определены со среднеквадратическими ошибками (СКО) массив Г|(n)!, j = 1^ J, n > 1, может содержать компоненты, не отождествля- емых ни с одним из элементов

E ( ⁿ ) ^ i

i = 1 _ I ,

n > 1, и наоборот.

Для идентификации объектов с однотипными признаками rI ⁽ n ) ] и rI⁽ n ) ], i = 1 ™ I , j = 1 ™ J , n > 1, по критерию минимума среднего риска R ps требуется установить принадлежность I компонентов rI in ) ], i = 1 ™ I , n > 1, определенных первым средством мониторинга, K i = I + J объектам

где R ₀ – положительно определенная величина, 5_a p — символ Кронекера, путем подстановки (5) в (2), а полученного результата в (1) находим правило отождествления объектов

( i' , k' ) = arg max P , _s

i = 1 ^ I , k = 1 ^ K_I

( I in ’;I ⁽ n ’ ) ■

из числа J зафиксированных или I пропущенных

С учетом (3) представим (6) в виде

вторым средством мониторинга с массивом зна чений ГI(П)!, k = 1™Ki, n > 1, при условии [6]

( i' , k' ) = arg max P_a, i = 1 ™ I , k = 1 ™ K_I

( I ! ^{n l} > ■ p |i * ;

I in ) l. (7)

^*

( i , k ) = arg min R p. ,                         (1)

i=1™ I, k=1™ KI где

^R ps = £ T;^Rik ^Pps ( ^{I (} n ) ; I ⁽ n ) )               (2)

i = 1 k = 1

Условная вероятность ситуации отождествле- ( n ) ния объектов с однотипными параметрами I _i

( n )                                                         ^ ^

и I k , i = 1 ™ I , k = 1 ™ K i , n > 1, находится как произведение вероятностей того, что при гипо-

R_ik – риск принятия решения об отождествле-

нии объектов с однотипными параметрами и _ I⁽ n ) !, i = 1 ™ I , k = 1 ™ K , n > 1,

E ^{( n} ) I _i

P ps ( I⁽ n ) ; I ^ ) ) = P ap ( I⁽ n ) ) ■ P | I ^ )| I⁽ n ) j    (3)

тезе отождествления пары объектов ( i , k ) значения I⁽¹ i ) , i = 1 ™ I , n > 1, принадлежат некоторой области Q ( n ) , n > 1, с размерами, определяемыми порогом принятия решения [3], в окрестности I kn ) , k = 1 ™ K i , n > 1, а любые другие значения

I ⁽ pn ) , p ^ i , p = 1 ™ I , n > 1, располагаются пределами [3; 7]:

за ее

– апостериорная вероятность гипотезы об ото-

ждествлении объектов с однотипными параметрами Г! ” ⁾~l и Г I k ⁾~l, i = 1 ™ I , k = 1 ™ K , n > 1,

определенная в соответствии с теоремой гипо-

тез [3],

^P ap ( ^I in ) ) ^-

априорная вероятность ус-

^P | ^{I (} n ⁾| ^{I ( n} ) }= ^P | ^I k^{n )}| ^{I (} iⁿ ) ; ^ ( n )}^{x х} П I ¹ - ^P ( ^I k^{n )}| ^I pn ) ; ^Q ( n )» ,      (8)

p = 1, p ^ i

ловия отождествления i -ого объекта, i = 1 ™ I ,

k = 1 ™ K ,

P

I

^{( n} ) k

E ( n )

^I i

условная вероятность ситуа-

ции отождествления k -ого, k = 1 ™ K , и i -ого,

i = 1 ™ I , объектов, выявленных различными

средствами мониторинга [4].

Ввиду того, что гипотезы, решения и ситу-

ации отождествления целей образуют полную

группу несовместных событий,

p I i ^{( n} ) E ^{( n} ))   _M   p  / E ^{( n} ). S ^{( n} )\

^P I ^I k ^I i I    ^{и   P} ps ( ^I i ; ^I k )

для ^P ap ( ⁱ⁽ " ) ) , выполняются

где p Г i (n) E (n). q ) _

^P I ^I k ^I i ^; ^ ( n ) I

Г f J ( n ) ; ( n T n r      ( r )

= J w | ^I k ^I i J П d ^I i , ^ ( n )                        r = 1

k = 1 ™ K , i = 1 ™ I ,    n > 1,

требования [4]:

ZX (K n > > - 1, ^ P I I k * I ( " > )- 1, i = 1                           k = 1

£ fx ( I ( ⁿ ' ;i ⁽ n ’ ) =1. i = 1 k = 1

Полагая, что риски принятия правильных решений равны нулю, а все неправильные решения приводят к одинаковым информационным потерям, т. е.

R ik = ^R 0 ( ¹ — 5 ii' )( ¹ — 5 kk' ) >                     ⁽⁵⁾

^{( n} ) k

E ^{( n} )

^I i

w

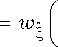
S ^{( n} ) ^I k

¥

^{( n} ) k

•

w I

E ^{( n} )

^I i

¥

^{( n} ) k

– закон распределения однотипных параметров

при априорной неопределенности их истинных значений ¥ kn ) , k = 1 ™ K , n > 1,

w

I

I

^{( n} ) k

_¥(_ n )

I                           x n 2"Z(" ‘k')

r = 1

x exp [- ]E ( I i -V kr ^d [2 jr ( a ( r ) ) 2

I r = 1                       / |_ r = 1

('

W Ц ) Ц I " i

.                           X

^tpif r=1

( n .    , .           . . . 9 / Г n             9

exp- ] ( S ir ) "» kr ) )     2 ] ( » i ) )

₂ r = 1                     / _ r = 1

– условные плотности вероятности признаков идентификации пары объектов ( i , k ) , i = 1 ™ I , k = 1 ™ K I , n > 1.

Вследствие априорной неопределенности параметров при вычислении апостериорной вероятности гипотезы об отождествлении объектов,

выявленных различными средствами монито-

( n )

ринга, истинные значения ¥ k ⁷, k = 1™ K , n > 1, в (10)–(12) заменяются оценками максимального правдоподобия [5]:

s⁽ n ) -(a⁽ n ¹) ^{- 2} + ] s⁽ iⁿ 4a⁽ n T

__________________________ i =1 ________________________

w ^{( n} )_ ,

^ k = 1

( a⁽ n -T + ] ( a⁽ n ) ) ^- 2 i = 1

при k = 1 ™ J ;

] ц I n ) , ( a I n ) ) ^{- 2}

= 1

объектов и больших ожидаемых погрешностях измерений могут быть достигнуты такие же значения вероятности (9), что и для близких зна-

( n ) чений ^ц V'

^{и [} l⁽ 1 n )

, i = 1 ^ I , n > 1, при малых

СКО a ⁽ n ) и a⁽ 1 n ) . Нормирующий множитель в (14) увеличивает информационные потери [3] для измерений, выполненных с низкой точностью [8; 9].

Полагая равными значения априорной вероятности условия отождествлении каждого i -ого объекта, i = 1 ^ I , с учетом (8)—(13) правило (7)

представим в виде

( i ', k ‘ ) = arg max P * | Ц — i = 1„. 1 ,       2

k = 1„. K I

I ⁽

i

где символ «*» означает, что условная вероятность (8) вычисляется при замене в (10) истинных значений признаков идентификации ^ -n ) их оценками максимального правдоподобия ^ kn ) , k = 1 ^ K I , n > 1.

2. Квазиоптимальный алгоритм отождествления объектов при структурно-системном мониторинге обстановки

] (a(nT i=1

при k = J + 1 ™ K i .

Алгоритм (15) позволяет выполнять оптимальное по критерию минимума среднего риска (1)

отождествление целей, выявленных совместно

функционирующими средствами мониторинга, в

условиях априорной неопределенности признаков идентификации.

Используя (10)–(13), несложно показать, что при отождествлении I объектов, выявленных первым средством мониторинга, с одним объектом, данные (сведения) о котором поступают от второго средства, закон распределения признаков идентификации (10) имеет вид

Однако для установления принадлежности

оценок максимального правдоподобия (13) пара-

( n ) метров ^ц у

^{и [} l⁽ kn )

, i = 1 _ I , к = 1 ^ K I , n > 1,

соответствующим объектам требуется провести

сравнение значений условной вероятности ситу-

w

s ( • )

E ^{( n} ) ^s i

ации отождествления

P _*

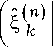
i = 1 ^ I , n > 1, для

2„ ] n ; [ ( a ⁽ r ) ) ² + ( „⁽ r ) ) ²

у r = 1 ^_

K i !

I ! ( K i — I ) !

s in)), к = 1™ Ki, возможных со-

четаний из K_I по I . В системах измерительносигнатурной разведки MASINT – Measurement

And Signature Intelligence, включающих в свой

n

] ( s ( ⁿ ) -s 1n ) )

r =1 ________________________

2 ] [ ( a ¹ , ^r) ) ² + ( a^) ) ²

r = 1 ^_

состав средства радиолокационного обзора, оптико-электронные, акустические, сейсмические и магнитометрические датчики [1], си-

Из (9) и (14) следует, что при существенном различии значений однотипных параметров

стемах территориального контроля, раннего обнаружения и распознавания подвижных наземных целей REMBASS – Remotely Monitored Battlefield Sensor System и SOTAS – Stand off Target Acquisition, где для добывания данных

(сведений) об обстановке применяются оптикоэлектронные, акустические и сейсмические разведывательно-сигнализационные приборы [1], активно-пассивных системах радиолокационного обзора воздушного пространства [10] значения I и K_I могут достигать нескольких десятков и сотен. Поэтому решение задачи отождествления объектов на основе (15) в реальном масштабе времени затруднено.

Для повышения быстродействия построенного алгоритма предлагается его квазиоптимальная модификация

( i " k " ) =

i ", i" = 1 ™ I , а за счет единичной ошибки отождествлена пара ( k ", i " ) , то объекты, образующие пару ( k', i ") также не подлежат правильному отождествлению.

3. Анализ характеристик отождествления объектов при априорной неопределенности однотипных параметров

Для анализа эффективности алгоритмов (15) и (16) на основе имитационного моделирования потока значений однотипных параметров [8; 9]

( n )

= arg max P* I s k 7 i=1™ I,     V k=1™ KI

I ⁽ n ) ^s i

найдены статистические характеристики ото-

p / =( n )

^P * ( ^S k

£ ( n )

^P * ( ^s k •

S⁽ n ^o, S⁽ n ⁾ ) = o

ждествления объектов по оценкам их координат

Согласно (16), при идентификации объектов

в матрице условных вероятностей P * | S ⁽ n )

। ⁽ n ) ^s i

( n = 2):

S( 1)= :x i,    si 2)= yi,    i = 1™ I, s k1)= X k,   S k2)= y k,   k = 1™ Ki .

k = 1 ™ K i , i = 1 ™ I , n > 1, находится наибольший

Область Q

ограничена окружностью радиуса R ;

элемент, соответствующий ситуации отождествления k '-ой и i '-ой цели, k = 1 ™ K i , i = 1 ™ I . Идентифицированные результаты заносятся в

при этом (9) имеет вид

список выполненных отождествлений, а из ма-

трицы условных вероятностей ситуаций отождествления исключаются элементы k '-ой стро

ки и i'-ого столбца; в модифицированной ма-

^P ( x k , yk | x i , ^y i ; ^q( 2 ) ) =

X k + R y k ⁺ ^ R 2 - ( ^X k - ^x i )                             (18)

= 2 j            j w ( x k, y k | x i, ij i) x x k - R         y k x dyjidxi,   i = 1™I, k = 1™Ki,

n трице P* ISk

S in ) I размером ( K i - 1 ) x ( I - 1 )

распределение w

снова осуществляется поиск наибольшего

( ^x k , y k I ^x i , y / i )

в явном виде

может быть получено из (10)–(12) путем замены

элемента. Указанные процедуры повторяются

L i = min ( I , J ) раз.

Исключение соответствующих строк и столб-

переменных (17) с введением унифицированных обозначений:

цов из исходной матрицы может выполняться пу-

тем обращения в нуль элементов P * I | ( n

I к( n ^{и P} * I ^s k

E (

i

I, k , k " = 1 ™ K , i , i " = 1 ™ I . При

этом общее число операций по отождествлению

объектов структурно-системного мониторинга

сокращается в L_I раз.

Квазиоптимальный характер алгоритма (16) обусловлен возможными пропусками подлежащих идентификации целей, поскольку в k "- ой строке и i "- ом столбце, исключающихся из матрицы (8), могут содержаться элементы, имеющие большие значения, чем оставшиеся в модифицированной матрице. В результате возможно появление кратных ошибок отождествления после единичного ошибочного решения. Если истинная идентификация должна быть выполнена для пар целей ( k ", i " ) и ( k ", i ") , k , k" = 1™ K i ,

- ( 1 )               - ( 2 )

^ i -^ x ,   'CT    =CT y , i = 1 ™ ¹ ,

⁽¹⁾ _ ^      ^ ⁽²⁾ _ ^      L. _ 1   _K

^CT k ^CT x ,     ^CT k ^CT y ,     ^k 1 ™ K I ,

при равной точности оценки однотипных параметров для всех I и K_I объектов.

Вероятность правильного отождествления объектов Р ₀ определялась как статистически

усредненное отношение числа правильно отождествленных целей к общему количеству выполненных отождествлений, вероятность ложной тревоги Р ₁ – как отношение математического ожидания ложно выполненных к общему количеству возможных ошибочных отождествлений [4; 9].

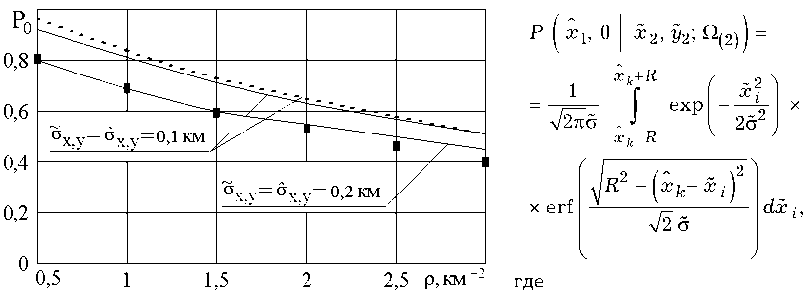
На рис. 1 приведены зависимости Р ₀ от плотности размещения объектов, выявленных первым средством мониторинга, p i в общей зоне ответственности средств мониторинга. Сплош-

a

Рис. 1. Зависимости вероятности правильного отождествления от плотности размещения объектов в зоне мониторинга обстановки

ной линией представлены результаты, полученные на основе алгоритма (15) при R = 2 д, где д = д2 + д2, a = с = 0,1 км и 0,2 км, xyx,y   x,y а пунктирной линией — при R = 3, 5 д. Черными квадратами обозначены значения Р0, найденные по правилу (16) при R = 2 д и дx y = д x у = 0,2 км. Вероятность ложной тревоги всюду составляет 0,01.

Из зависимостей следует, что при R = 2 д и указанных значениях <5 xy и д xy увеличение плотности объектов с 0,5 км ^{- 2} до 2 км ^{- 2} приво-

2    - erf (a) =       e t dt

n

– функция (интеграл) ошибок, а условная вероятность ситуации отождествления (8) определяется выражением [7]

P ( x 1 , 0 I x 1 , y 1 )

г г

¹ - exp

R ²

2д 2

X

-

2пд

X k + R

I

дит к снижению вероятности правильного отождествления с 0,9 до 0,65. С увеличением R до 3,5 д при р = 0,5 км-2 величина Р0 возрастает до 0,95, а при д™,, = д = 0,2 км, R = 3,5 д и x,y      x,y р = (0,5 ...2) км 2 лежит в пределах 0,55^0,8 при вероятности ложной тревоги, не превышающей 0,02.

Установлено, что при R < 2 д вероятность правильного отождествления объектов даже

X erf

X k - R

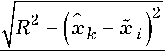
1    1

<3

I

7 I

при значительных расстояниях между ними

Как показано в [7], с увеличением расстояния между объектами x k с 3,3д до 4д при R / д = 4 значение (22) повышается с 0,6 до 0,8, а за счет изменения R от 4д до д при x к /д = 3,3 — возрастает с 0,6 до 0,9.

ограничивается вероятностью попадания пара-

метров идентификации в область ^ ( 2 ) ■ Поэтому для достижения показателя Р 0 = 0,95...0,99 при Р ₁ = 0, 01 требуется высокая (не менее 0,1 км) точность местоопределения объектов [7; 9].

В частном случае отождествления объектов по оценкам координат ( Х ^ y 1 ) и ( x 1 ; у 1 = 0 ) при наличии вскрытых двумя средствами мониторинга мешающих целей в точках ( x 2 ; y 2 ) и ( x 2 = 0; у 2 = 0 ) условная вероятность группирования однотипных параметров (18) в предположении, что д = д X + д У ^ 0, т. е. значения ( x 1 ; 0 ) и ( 0; 0 ) близки к истинным, имеет вид [7]:

Квазиоптимальный алгоритм отождествления (16) сохраняет работоспособность при малой плотности размещения идентифицируемых объектов и высокой точности оценки однотипных параметров. При р = ( 2 ... 3 ) км ^{- 2} различие величин Р ₀, найденных на основе (15) и (16) составляет 0,03…0,05 ввиду пропуска подлежащих отождествлению целей на этапе формирования модифицированных матриц условных вероятностей ситуаций отождествления. Установлено, что за счет уменьшения СКО д xy и д xy до 0,1 км при р = ( 2 ... 3 ) км ^{- 2} применение квазиопти-мального алгоритма отождествления объектов

P ( x 1,01

x 1 , У ь ^q ( 2 ) ) = 1 - exP

' R ²

—

2д 2

,

приводит к получению заниженных значений Р ₀ на 0,02…0,03.

Заключение

Таким образом, с использованием критерия минимума среднего риска [3; 4] и оценок максимального правдоподобия однотипных параметров [5] выполнен синтез алгоритма отождествления объектов при структурно-системном мониторинге обстановки в условиях априорной неопределенности признаков идентификации [5; 6]. Показано, что при равенстве нулю рисков принятия правильных решений и одинаковых информационных потерях для всех неправильных решений, а также равных значениях апостериорных вероятностей гипотез об отождествлении идентификации подлежат объекты с максимальной условной вероятностью ситуации отождествления. При этом априори неизвестные значения признаков идентификации, обусловленные, в том числе, их пропусками в различных средствах мониторинга, требуется заменять оценками максимального правдоподобия.