Оптимальное количество аналогов в условиях неоднородности рыночных данных

Анализ и обработка рыночной информации является неотъемлемой составляющей при определении рыночной стоимости объекта оценки в рамках любого из трех классических подходов к оценке – затратного, сравнительного и доходного. При этом метод сравнения продаж в той или иной степени применяется при использовании каждого подхода: затратного – при оценке земельного участка как свободного, доходного – для определения рыночной величины арендной платы. Но наибольшее распространение в практике оценки объектов недвижимости получил метод сравнения продаж в рамках сравнительного подхода. Суть метода сводится к тому, чтобы найти из числа недавно проданных или выставленных на продажу объектов недвижимости достаточное количество объектов, сопоставимых по ценообразующим факторам с объектом оценки (см. [1, п. 12; 2, п. 22б]). Далее каждый объект-аналог сравнивается с объектом оценки по ценообразующим факторам, и удельный показатель корректируется по выявленным различиям для того, чтобы приблизить объект-аналог по своим характеристикам к объекту оценки ¹ .

Отметим, что применение этого подхода возможно при условии, что в распоряжении оценщика имеется подробная информация об объектах-аналогах, в том числе обо всех ценообразующих параметрах, по которым будет проводиться сравнение (их полный перечень для оценки объектов недвижимости приводится в пункте 22 Федерального стандарта оценки № 7; далее – ФСО № 7). При этом объекты-аналоги должны относиться к одному и тому же сегменту, а сделки с ними должны осуществляться на типичных для этого сегмента условиях.

В различных источниках указано требуемое количество объектов-аналогов (обычно 5–6), и это количество не связывают ни с характером данных, ни с активностью рынка.

На первый взгляд метод представляется достаточно простым и понятным. Его практи- ческая реализация не вызывает каких-либо затруднений. Однако если посмотреть, как «ведет себя» погрешность оценки при увеличении общего объема рыночных данных в реальных условиях, то, как будет показано далее, это «простое решение» может привести к серьезным ошибкам.

Если имеется возможность собрать данные о ценах предложений сходных объектов, которые по всем ценообразующим параметрам полностью идентичны объекту оценки, то сформированный по таким объектам набор цен образует однородную совокупность. В этом случае точность, характеризуемая погрешностью (неопределенностью) результата оценки, определяется стандартной неопределенностью или интервалом, в котором может находиться рыночная стоимость. В соответствии с требованием пункта 30 ФСО № 7 такой интервал требуется приводить в отчете об оценке. Отметим, что в случае однородной выборки в качестве такого интервала может использоваться доверительный интервал для среднего или для медианы в зависимости от того, как определяется рыночная стоимость.

Использование 5–6 аналогов позволяет получить удовлетворительные по точности оценки рыночной стоимости объекта оценки. Однако на практике чаще всего собрать достаточную по объему выборку из таких цен не представляется возможным. Прежде всего это относится к ситуациям, связанным с оценкой низколиквидных, узкоспециализированных или уникальных объектов, а также объектов, расположенных в отдаленных районах или при оценке на дату в прошлом. В этом случае приходится привлекать данные об объектах, отличающихся одним, двумя и более параметрами. Ряд цен таких объектов уже не может рассматриваться как однородная выборка. Образованная таким образом выборка характеризуется увеличенным разбросом цен. Причем разброс цен увеличивается по мере привлечения объектов-аналогов, отличающихся от объекта оценки большим количеством ценообразующих параметров. Это приводит к тому, что погрешность (неопределенность) оценки при увеличении объема выборки растет. В некоторой степени преодолеть эти эффекты можно, выполняя необходимые корректировки рыночных цен. В этом случае мы получаем квазиоднородную выборку, и увеличение ее объема до определенных пределов с соответствующим снижением погрешности оценки становится возможным.

После проведения необходимых корректировок определяется среднее (или медиана) цен сделок/предложений, которое и принимается в качестве результата оценки рыночной стоимости объекта оценки. При этом, однако, погрешность результата оценки может существенно отличаться от ситуации, характерной для однородной выборки. Она будет зависеть от вероятностного распределения скорректированных цен, количества корректировок по каждому объекту-аналогу и уровня неопределенности используемых корректировок.

Вопросы влияния неоднородности исходной выборки рассматривались в отдельных публикациях. Особенно следует отметить работу Н.П. Баринова и Д.А. Корнилова [3], в которой обозначена проблема высокой неопределенности получаемых результатов индивидуальной оценки недвижимости и на конкретном примере показано, насколько могут отличаться результаты оценки одного и того же объекта недвижимости разными оценщиками. Отметим, что в ходе практической работы по анализу отчетов об оценке мы также наблюдали аналогичную картину: при оценке одного и того же объекта недвижимости 14 разными оценщиками итоговая рыночная стоимость объекта (после корректировки на дату) отличалась более чем в 2,6 раза (!).

Также следует отметить работу Н.А. Пущаенко [4], в которой автор рассуждает о «точности» (неопределенности) оценки рыночной стоимости в зависимости объема информации и на примерах показывает, что ширина интервала неопределенности оценки стоимости может быть равна и даже превышать ширину интервала вариации цен аналогов. В статье показано, что вклад в неопределенность оценки итоговой стоимости объекта вносят как первоначальные цены выборки и их распределение, так и корректирующие коэффициенты, однако конкретные методики определения этого влияния не приводятся.

Многие авторы, как зарубежные, так и отечественные, в своих работах поднимали вопросы, связанные с процедурой расчета корректировок. Эта тема достаточно обширная и заслуживает отдельного внимания в рамках настоящего исследования, поэтому мы ограничимся упоминанием лишь некоторых источников.

Рейчел Мэсси в своей статье «Корректировка, часть 2: Какие методы корректировок наилучшие на вашем рынке?» [5] пишет не только о традиционных методах расчета корректировок, которые используются американскими оценщиками на практике (метод парных продаж, статистические методы, интервью покупателей, большие данные (big data) и т. д.), но и о программе для расчета корректировок с помощью регрессионных моделей. Основываясь на собственном практическом опыте, Р. Мэсси выводит основные правила проведения корректировок.

• 1)    не рекомендуется применять постоянно одни и те же методы для расчета разных корректировок. Это правило продиктовано тем, что различные ценообразующие параметры не единообразно вносят свой вклад в стоимость объекта недвижимости, они являются случайными величинами, и могут быть распределены по разным законам;

• 2)    не следует корректировать каждый объект-аналог в «сетке сравнения продаж» ² , что еще раз подтверждает то, что использование аналогов, отличающихся от оцениваемого объекта по многим параметрам, отрицательно влияет на точность итогового результата оценки;

• 3)    методика расчета корректировок не обязательно должна подчиняться общим требованиям к проведению оценки стоимости. Например, для расчета корректировок допускается использование ретроспективных данных о продажах, что при определенных условиях может оказаться даже более эффективным, чем использование текущих данных о продажах.

Автор показывает на примере, как с использованием данных о прошлых продажах были построены ценовые отношения, которые на протяжении десяти лет на конкретно взятом рынке остаются стабильными. Такие отношения и следует использовать в качестве процентных корректировок.

Ричард Хагар ³ насчитывает более 25 различных методов для расчета корректировок, базирующихся на трех основных подходах к оценке, а также статистических методах. На своих вебинарах (см. [6]) он рассказывает обо всех этих методах, а также о том, как использовать программный продукт MS Excel для расчета корректировок.

В книге Марка Раттермана «Оценка методом сравнения: Аналитика и логика жилой недвижимости» [7] более чем на 30 страницах представлены различные методы расчета корректировок с математическими иллюстрациями. М. Раттерман обсуждает как плюсы, так и минусы для каждой возможной методологии. В книге рассматриваются и другие темы, например подбор аналогов, которые также очень полезны для практикующего оценщика.

В книге Франка Харрисона «Нелегкая оценка: креативные способы оценки сложных жилых объектов» [8] не затрагиваются математические детали методов, но содержатся полезные рекомендации о том, как подойти к оценке нетипичных для конкретного рынка объектов недвижимости.

Авторы настоящей статьи в работе «Рекомендации по определению и обоснованию границ интервала, в котором может находиться стоимость объекта оценки (пп. 25 и 26 ФСО № 1 и п. 30 ФСО № 7) 2017 г.» [9] предложили методику расчета нижней и верхней границ интервала величины рыночной стоимости, определенной в рамках сравнительного и доходного подходов с учетом количества объектов-аналогов и неопределенности корректирующих коэффициентов, а также методику принятия решения относительно существенности/несущественности различия результатов оценки стоимости, полученных с использованием различных подходов (методов). Вопросы анализа рыночной информации с точки зрения ее качества и повышения точности оценки объектов недвижимости также рассматривались авторами в рамках доклада на Девятой международной научно-методической конференции «Стоимость собственности: оценка и управление» [10].

В настоящей статье развивается идея о том, что эффективное использование метода сравнения продаж предполагает определение неопределенности (погрешности) результата оценки, что, в свою очередь, требует анализа исходных рыночных данных, степени сходства аналогов с объектом оценки, определения в каждом конкретном случае количества аналогов, которое целесообразно использовать. Мы рассмотрим, как неоднородность исходных данных влияет на точность оценки, а также проведем анализ возможностей повышения точности результата оценки на основе использования метода сравнения продаж в реальных условиях неоднородности исходных данных.

Точность результата оценки

Обычно в качестве рыночной стоимости в рамках метода сравнения продаж принимается среднее значение цен объектов-аналогов, рассчитанное по формуле (см. [12]):

n

V o = 1 ^ V , n i = 1

где V_o – результат оценки рыночной стоимости;

V_i – цены объектов-аналогов;

n – количество объектов-аналогов.

Также может использоваться другой показатель центра распределения (например медиана). По существу, это ничего не меняет.

Мерой точности полученной оценки является погрешность (стандартная неопределенность – в терминах современной теории измерений), которая по смыслу является величиной, обратной точности. В качестве меры неопределенности результата оценки обычно используется стандартная ошибка среднего. Стандартная ошибка в математической статистике – это величина, характеризующая стандартное отклонение выборочного среднего, рассчитанное по выборке из генеральной совокупности. Другой мерой неопределенности результата оценки является доверительный интервал, который указывает диапазон, в котором с заданной вероятностью (называемой доверительной вероятностью) может находиться оцениваемая стоимость объекта оценки.

Стандартная ошибка s зависит от стандартного отклонения совокупности ( S ), из которой получена эта выборка:

S =

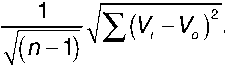
Она также зависит от количества объектов-аналогов, которые используются при определении рыночной стоимости, и рассчитывается по формуле:

G =

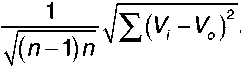
Неопределенность результата оценки, помимо стандартной ошибки, может быть характеризована величиной доверительного интервала:

[Vo – Δ, Vo + Δ], где Δ – ширина полуинтервала.

Ширина полуинтервала Δ определяется исходя из заданной величины доверительной вероятности и принятого закона распределения оценки известными методами математической статистики и может быть определена при помощи средств MS Excel. Обычно в качестве распределения случайной величины – среднего значения, используется нормальное распределение. В этом случае ширина полуинтервала пропорциональна стандартному отклонению △ = 5 * о . Если 5 = 2, то относительно рассчитанного таким образом доверительного интервала можно утверждать, что оцениваемая рыночная стоимость находится внутри интервала с вероятностью 0,95.

Анализ зависимости стандартной ошибки от количества исходных данных в случаях однородной и неоднородной выборок

Рассмотрим идеальную ситуацию, когда подобранные объекты-аналоги сходны с оцениваемым объектом по всем ценообразующим характеристикам. В этом случае можно говорить, что мы имеем дело с гомогенной или однородной выборкой.

Как видно из формулы (2), при увеличении объема однородной выборки величина стандартной ошибки уменьшается, соответственно уменьшается и доверительный интервал. С точки зрения оценки это утверждение означает, что при добавлении новых однородных объектов-аналогов точность результата оценки повышается. Теоретически при заданной точности можно определить количество необходимых аналогов для оценки (см. рис. 1).

Однако, как уже было указано, на практике в большинстве случаев не удается собрать данные об аналогах, сходных с объектом оценки по всем характеристикам, и оценщик вынужден привлекать объекты, отличающиеся одним, двумя, а иногда и более параметрами. При этом возникают два эффекта:

• •    увеличивается количество данных в выборке, и, как следствие, стандартная ошибка и доверительный интервал уменьшаются;

• •    привлечение новых объектов-аналогов, отличающихся от объекта оценки сначала одним, затем двумя и т. д. параметрами, все в большей степени нарушает однородность исходных данных, что ведет к повышению уровня неопределенности результата оценки.

В результате оказывается, что увеличение количества данных в какой-то момент (после 4-х объектов) становится неоправданным, поскольку дальнейшее увеличение выборки приводит к увеличению стандартной ошибки (см. рис. 2).

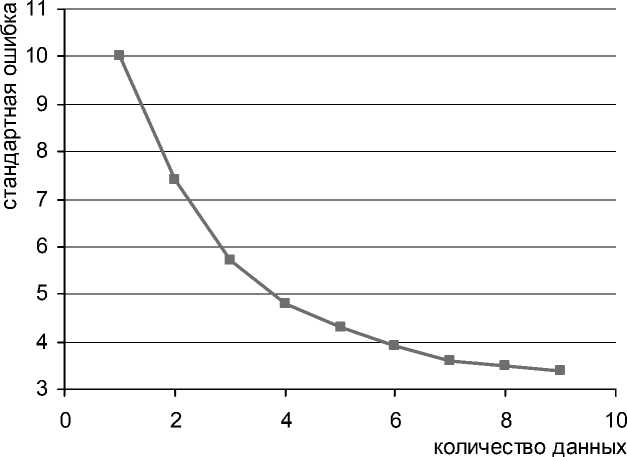
Рис. 1. Зависимость стандартной ошибки результата оценки однородной выборки от количества данных (в нашем случае – объектов-аналогов)

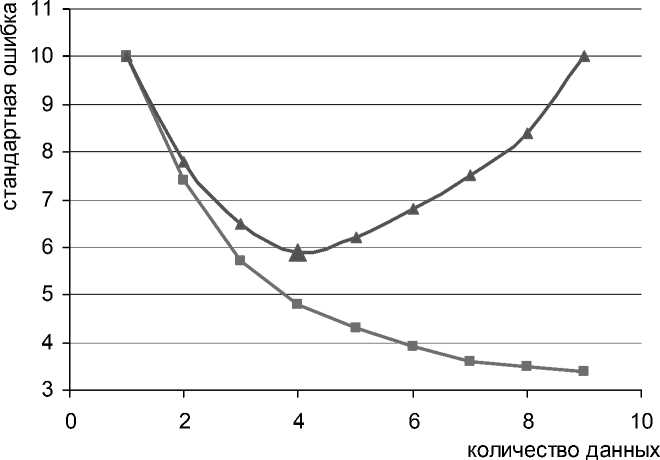
—■— однородная выборка   * неоднородная выборка

Рис. 2. Зависимость стандартной ошибки однородной и неоднородной выборок от количества данных

Как видно из графика, представленного на рисунке 2, минимум стандартной ошибки при 4-х аналогах, а при увеличении количества данных стандартная ошибка оценки начинает расти. На практике в условиях неразвитого рынка стандартная ошибка оценки может расти сразу после одного, двух аналогов.

Формирование выборки для оценки методом сравнения продаж в реальных условиях

Как отмечено в пункте 22б ФСО № 7, «в качестве объектов-аналогов используются объекты недвижимости, которые относятся к одному с оцениваемым объектом сегменту рынка и сопоставимы с ним по ценообразующим факторам» или параметрам сравнения. При этом степень сопоставимости (сходства) аналога и объекта оценки будет разная в зависимости от того, по какому количеству параметров сравнения они будут различаться. Наибольшее сходство имеет место для объектов-аналогов, ценообразующие параметры для которых полностью совпадают с соответствующими параметрами объекта оценки. Такие объекты будем называть прямыми аналогами.

Как мы уже отмечали, в условиях недостатка прямой рыночной информации, то есть данных о ценах, относящихся к сходным по всем параметрам объектам, оценщик вынужден привлекать данные о ценах дополнительных объектов, отличных от объекта оценки по тем или иными характеристиками (площадь, местоположение, состояние, этаж расположения и т. д.). Вновь сформированная таким образом выборка становится неоднородной, отличается более высоким стандартным отклонением, чем начальная однородная выборка. В зависимости от того, из каких объектов сформирована выборка цен продажи, можно говорить о степени однородности выборки. Цены прямых аналогов образуют однородную выборку. Обычно увеличение выборки осуществляется следующим образом: сначала включаются прямые аналоги, затем добавляются аналоги, отличающиеся одним параметром сравнения, потом отличающиеся двумя параметрами и т. д. При этом сходство с объектом оценки снижается по мере увеличения числа параметров сравнения, по которым объект-аналог отличается от оцениваемого объекта.

Каждую выборку будем характеризовать количеством входящих в ее состав аналогов и уровнем неоднородности данных, который будем измерять максимальным числом ценообразующих параметров, по которым объекты-аналоги отличаются от объекта оценки. При увеличении объема выборки посредством добавления дополнительных объектов-аналогов, отличных от объекта оценки на определенное количество параметров, увеличивается и уровень неоднородности данных. При этом выборка с более высоким уровнем неоднородности будет включать и предыдущие объекты-аналоги с меньшим уровнем неоднородности. Таким образом, по мере привлечения новых аналогов увеличивается объем выборки (количество аналогов) и одновременно растет уровень ее неоднородности (см. табл. 1).

Таблица 1

Характеристика уровня неоднородности выборки объектов-аналогов

Уровень неоднородности выборки	Характеристика объектов-аналогов, включаемых в формируемую выборку (наличие параметров сравнения, отличающихся от таковых у объекта оценки)
A 0	нет
A 1	не более одного
A 2	не более двух
A 3	не более трех
A k	не более k

В отличие от однородной выборки, которая может быть описана одномодальным распределением случайных величин, образованный таким образом набор исходных данных представляет собой выборку из композиции распределений случайных величин. Стан- дартное отклонение для такой выборки будет больше, чем по отдельным однородным выборкам. Это будет проиллюстрировано далее.

Рассмотрим пример, иллюстрирующий основные положения материала, изложенного в настоящей статье.

Исходные данные

Объект оценки относится к сегменту рынка «универсальные производственно-складские объекты». Приведем его основные ценообразующие параметры, которые будут рассматриваться в рамках нашего исследования:

• 1)    общая площадь – 1 200 квадратных метров;

• 2)    материал стен – сэндвич-панели;

• 3)    физическое состояние – удовлетворительное;

• 4)    характеристики местоположения:

• •    численность населенного пункта, в котором находится объект оценки, – 250 тысяч человек;

• •    средняя заработная плата в населенном пункте – 28 тысяч рублей в месяц;

• •    территориальная зона нахождения объекта – районный центр с развитой промышленностью.

Подбор объектов-аналогов для объекта оценки

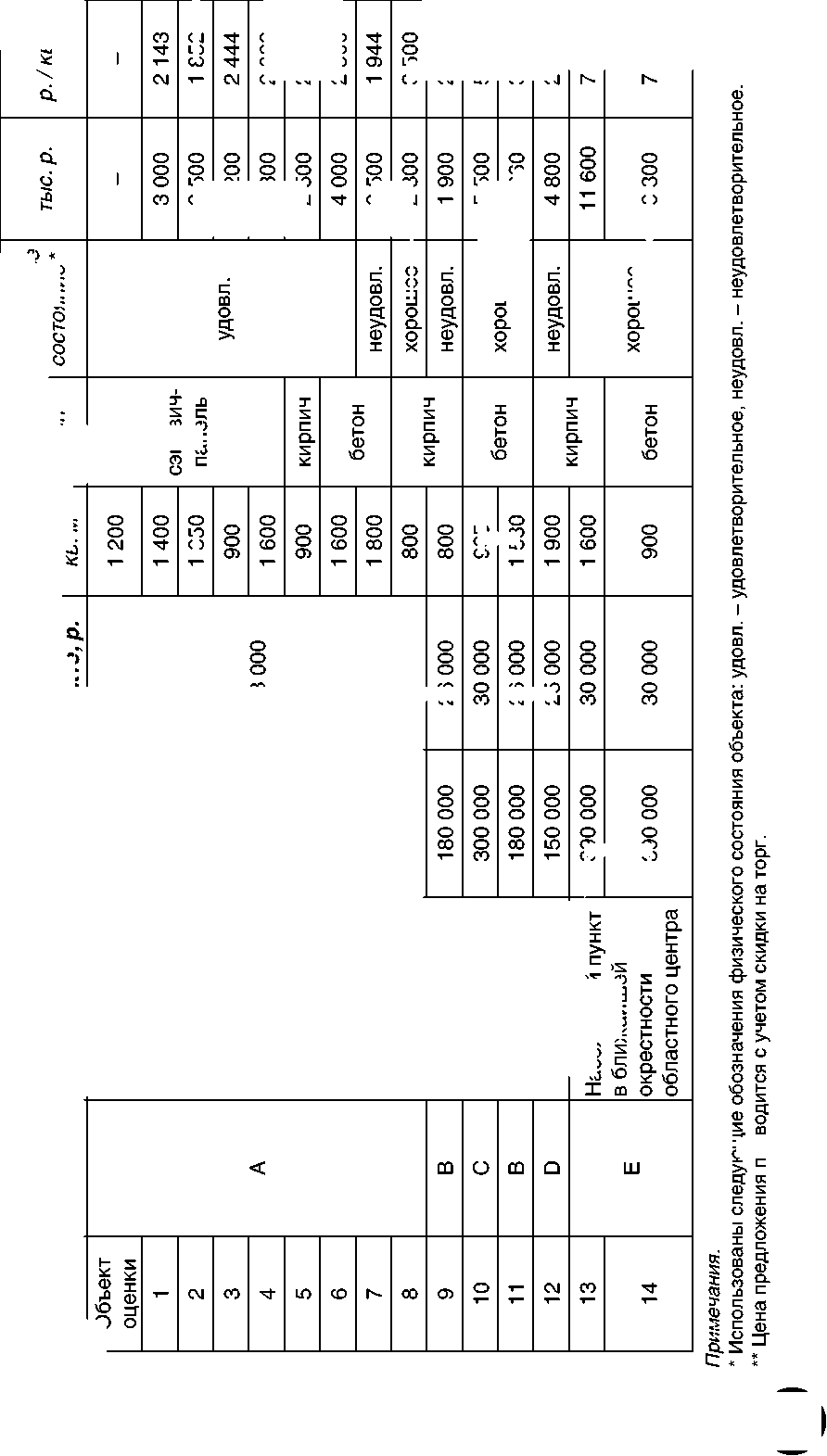
Предварительно был проведен обстоятельный анализ приведенных данных, из которого следует, что прямых аналогов, расположенных в населенном пункте объекта оценки и в то же время сходных по всем ценообразующим параметрам с объектом оценки, найдено всего 2 (см. табл. 2, аналоги № 1 и 2). Однородную выборку объектов-аналогов, включающую всего два объекта-аналога, следует признать недостаточной, поэтому предлагается расширить выборку за счет привлечения данных об объектах, отличающихся от объекта оценка одним, двумя и т. д. параметрами сравнения. Анализ рынка позволил подобрать объекты, сходные с объектом оценки (табл. 2).

Таким образом, мы будем формировать неоднородную выборку, постепенно переходя на новый уровень неоднородности данных (см. табл. 3).

На основании данных о ценах объектов недвижимости, сходных с объектом оценки, но отличающихся от объекта оценки по некоторым параметрам сравнения, можно сформировать различные выборки, каждая из которых характеризуется своим уровнем неоднородности. В таблице 3 приводятся сводные данные об уровнях неоднородности подобранных объектов-аналогов.

Итак, были получены шесть выборок, отличающихся количеством данных (объемом выборки), уровнем неоднородности и, соответственно, величиной рассеивания цен, измеряемого стандартным отклонением, рассчитанным по формуле (1). Как и следовало ожидать, стандартное отклонение неоднородной выборки зависит от ее уровня неоднородности. Как видно из рисунка 3, по мере увеличения уровня неоднородности стандартное отклонение растет. График зависимости стандартного отклонения от уровня неоднородности А _i , рассчитанный по данным приведенного примера, показывает, что разброс удельных цен объектов, принятых в качестве аналогов (выборочное стандартное отклонение), растет при переходе от более низкого уровня неоднородности к более высокому.

Таблица 2

I i

§ ф ст о 5 се CD л со о

Е

>с

о

? ср >с 5 Се CD Л со о ><

§ о со $ о со о со о CD

eg.

в Ф >0 О о § о X I Я

h

о i CD 5 X

co

CM co

CM со со

LO см

LO со см

LO см

LO см со LO LO

§

LO см

CD X X DC ф 3 'S 05

CX4±30HH9Lrmi4IAI0du

MOinaeBd о dmeh И1чнноивс|

CM

CD со см LO со

LO со ф т 05

LO со со LO

LO см

00 со

5 X

5 со ф ф

,Ф

О

I о 3

о

X 05 Н СО о

I CD

S р §

CD о 5

н о

ф

§ о

CD S ф

X Ф X

Ф

!

о

к I е

см со со

со см LO

Е о

§ X ^ X

§

О

в Ф >0 о о

ю см

см CM

со со

LO см

ю со

со см

LO LO

со О)

LO

ф ф

Ф Ф

со см

со см

LO со CD

со см

CD со

ф X ф о 05

£ 5 со о

Е о