Оптимальное планирование по критерию максимума ожидаемой эффективности

DOI:

На первый взгляд представляется, что хотя бы для предприятий, из года в год выпускающих стабильную по составу продукцию, спрос на результаты улучшающих НИОКР может быть оценен на основе прямой статистической обработки

временных рядов отчетных данных. На самом деле такой подход мало эффективен, причем не только в силу обычной недостаточности статистических данных, но и ввиду принципиальных организационно-экономических свойств НИОКР, в частности, значительной системности и неоднородности их результатов.

То же подтверждает и существующая, хоти и весьма ограниченная, статистика. Так, показано, что вид эмпирических функции распределения фактического выполнения по экономическим показателям, утвержденным в плане, примерно соответствует показанному на рисунке 1, причем доля случаев невыполнения – не более 3–5 %. В то же время для других показателей характерным является нормальный разброс относительно прогнозируемого в плане уровня.

Существенно, что такая закономерность подтверждалась и для одного и того же экономического показателя, но переходившего из разряда «утверждаемых» в разряд «неутвер-ждаемых» (например, для производительности труда персонала проекта).

Таким образом, прямая статистическая оценка даже для предприятий с устойчивой структурой производства мало полезна для поставленной задачи. Тем более нет реальных оснований пользоваться ею для предприятий-инноваторов с резко меняющейся технологиями либо с появляющимися инновационными продуктами.

Единственной возможностью при этом представляется расчетная оценка функции распределения фактического выпуска на основе математической модели производства, связывающей экономические показатели с располагаемыми уровнями ресурсов. Источником неопределенности при этом становятся флуктуации уровней ресурсов, не зависящие от плана НИОКР. Возможность статистической обработки этих флуктуаций для оцен- ки вероятностных характеристик обычно существует. Хотя, конечно, и здесь имеют место и принципиальные, и чисто вычислительные трудности, но в дальнейшем эти характеристики будут считаться известными. Для демонстрации методики рассмотрим первоначально простейшую модель, в которой уровень только одного из ограничивающих ресурсов является случайным, а производство использует только один технологический способ.

Обозначим интенсивность способа (объем выпуска) через х , затраты ресурса на единицу выпуска - а , располагаемое количество ресурса - го , прибыль на единицу - с . Тогда при плановой интенсивности х _п плановая прибыль П_п равна с х п , причем реализация х f ограничена в силу ограниченности ресурса условием х f < го/ а , а также, в силу иных детерминированных ограничений, условием 0 < х f < х .

Плановое решение реализуется только в пределах действительного наличия ресурсов, то есть фактическая прибыль П _f , равна: f        щ ]

П f = c min | ч_п, ч, б j .             (1)

Таким образом, фактическая прибыль является функцией не только внешних случайных факторов, но и принимаемого решения. Функции типа (1), выражающие зависимость показателя выпуска как от факторов, определяющих условия производства, так и от планового решения, в дальнейшем будем именовать планово-производственными функциями.

В отличие от принимавшегося выше, распределение фактического значения прибы-

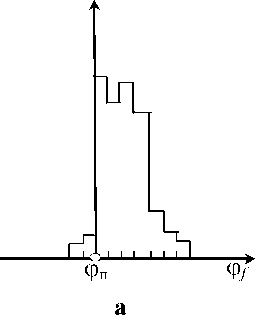
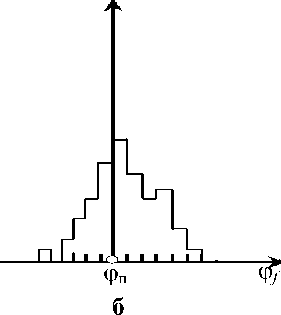
Рис. 1. Фактическое значение эффективности деятельности предприятия для показателей, утверждаемых планом ( а ) и не утверждаемых планом ( б )

Примечание. Составлено авторами.

ли само по себе оказывается зависящим от планового решения как от параметра.

В силу условия (1) имеем при

П_п = c ч _п ч <  с ч :

где п_п = cx _п< cx (можно считать, что щ < ax , поскольку в противном случае недетерминированность несущественна).

P { п f < и}   W f ( ж,П п ) = <

1       ж> пп

W щ [ бж), ж<п п

Именно такой закон распределений и должен быть теперь использован для оценки ожидаемого значения функции эффективности F ( п _f , п п ) :

м { F ( п f , п п ) } = | F ( ж п п ) dW f ( ж п п ) .    (3)

В соответствии с представленной концепцией плановое решение, то есть в данном случае планируемую интенсивность использования производственного способа, целесообразно искать как решение задачи:

Если функцию эффективности принять в виде функции стимулирования типа (5), то, как нетрудно убедиться, оптимальный план по прибыли должен быть

„          • f c f        k"- k Л 1 ™ п„ = cx„ = mrn<— щ+ м„1п------ ,cx H (8)

п п        [ a I”         k--1 ), J то есть совпадать с решением задачи:

max (пп = cxn / ax„ < щ+ м-'ln — i п       п п           щ т -7 *

k -1

0 <  x _п<  x } .

max [м ( F ( п f , ^) } =

= 1

^F ( ж ^п п ) d W f ( ж ^п )

п п

= с ч_п<  с ч

.

Если бы планирование велось по детерминированной схеме с ориентацией на средний уровень ресурсов m _щ = щ + м щ , то использовалась бы почти та же формулировка. Ясно также, что план, максимизирующий ожидаемую эффективность, совпадает с планом-решением задачи:

max cx { ax <  щ } >  1 - г, 0 <  x <  x J . (10)

Очевидно, что для окончательной формулировки задачи нет необходимости в предварительном вычислении функции распределения фактической прибыли, поскольку задача (4) эквивалентна следующей:

max Л F ^f б щ с Ч п ) dW щ ( щ ) /0 <  Ч п <  ч [ , (5)

где W _m , как и ранее, - заданная функция распределения располагаемого уровня ресурса ю .

Приведем пример вычисления оптимального плана для случая смещенного экспоненциального распределения ю :

W W ( Ж = 1 — exp [- м_щmax ( ж - щ 0 ) ] ,    (6)

где щ – гарантированный нижний уровень располагаемого ресурса; м щ¹ - среднее (и среднеквадратичное) значение случайного дополнения к нему.

В силу равенств (3) и (6) распределение фактической прибыли дается формулой:

W f ( ж, п п ) =

= <

- exp

-мщmax

a

- ж- щ,0 c

^ж >^п п

, ж< пп,

Однако значение «допустимого риска» у принимается не произвольно, а равным y o _p t и, следовательно, зависящим от параметров функции стимулирования.

Перейдем далее к рассмотрению многомерных задач, где ситуация значительно сложнее. Действительно, неясно, какой будет структура фактического выпуска, если окажется, что для выполнения планового задания НИОКР будет недостаточно ресурсов, или, напротив, после выполнения планового задания еще останутся ресурсы, достаточные для дополнительного выпуска.

Построение планово-производственных функций (п.п.ф.) вида f xf = xf (xп ,щ),

1^п f =^п f ^{( x} п ^,щ)^{, (11)} где x _П – плановый уровень интенсивности производственных способов; ю - случайные уровни располагаемых ресурсов; x_f , П _f – фактические интенсивности и прибыль, требуют введения дополнительной информации о способе реализации планового задания, не содержащейся в соответствующей статической детерминированной модели системы.

Пусть а ,_у , i = 1, ..., m ; j = 1, ..., n , - затраты ресурса i при единичной интенсивности способа j . Тогда для любой реализации должны выполняться соотношения:

^ач f - £ n _{= l} a ij x fj - Щ, * = 1, ..., m ,       ⁽¹²⁾

где а¹ - { a j , j = 1, ..., n } .

Причем далее и качестве гипотезы следующий вид п.п.ф:

где

p = min

1 щ - ах ’ а* ( х _п - х )

i = 1, ..., m

x f = ^СЧ и ,

где p - случайная величина:

с = min *

1,^ , * = 1, a x _n

.., m

Очевидно, что вектор x _f определенный в силу равенств (13) и (14), удовлетворяет условиям соотношения (12) и условию x_f е X , если х п е X и 0 е X , а X - область, определяе-

мая детерминированными ограничениями. Принятую формальную гипотезу можно назвать гипотезой сохранения структуры плана или гипотезой равномерности выполнения планового задания. Последнее наименование связано с такой интерпретацией. Предположим,

Формулы (16) и (17) могут быть интерпретированы как следствие гипотезы выполнения обязательного задания в первую очередь, а остальных заданий – равномерно.

Если принята та или иная гипотеза, определяющая вид п.п.ф., то далее построение плана, обеспечивающего максимум ожидаемого значения функции эффективности, производится чисто формально, как и в одномерном случае.

Предположим для простоты, что величины взаимно независимы, и используем формулу

W ( о ) = 1 -Ц.[ 1 - W »] ,       (18)

справедливую, если х = min*3 j,              (19)

а п * независимы и распределены согласно W-A о ) .

Поскольку в силу равенств (13) и (14)

что плановое задание x _П выполняется в течение планового периода длительностью Т равномерно, а работы по плану продолжаются вплоть до момента исчерпания какого-либо из ресурсов или выполнения плана. Тогда затра-

п           т I. щ - ах            I п f = Схх, =ппmini1,-=*-------, i = 1, ..., m i,(20)

[ a (х п- х)             J где c = (cj) – вектор с элементами, равными прибыли при единичном использовании способа j, то

W f ( ж п п ) =

ты i -го ресурса в единицу времени равны 1 i

—ах _п , а фактическая продолжительность времени работы Т _f должна удовлетворять условию T _f = T min 1,-щ- , а следовательно, факти- L а'х _п ]

=1 1

1 -п * : .

1 I Ж i

^{1 -} W “ i l тТ^ах

\^п п

,

ж >^п п ж < п_п

Tf ческое выполнение равно xf =   п, что и при водит к равенствам (13) и (14).

Можно несколько обобщить гипотезу сохранения структуры плана следующим образом. Пусть щ - нижний гарантированный уровень наличия ресурсов, х – обязательная

Примем в качестве функции эффективности функцию F (П_П, П _f ) типа (15). Тогда задача выбора оптимального плана приобретает вид:

max ^[ ( 1 + б в И п ) P { п f >п_п } / п_п = сх _п , х _п е X ] ⁽²²⁾

Отметим, что в силу разрывности

W f ( ж, ^п п ) при ^Z = П п

для выполнения компонента плана, заведомо обеспеченная ресурсами, то есть

Ах <  щ .                  (15)

Р { п f > п п } = 11ш ж .   [ 1 - W f ( ж, п п ) ] =

^Ж■^{И и}                         (23)

= п * =, [ 1 - W _w ( а'х „ ) ] .

Примем, что

X f = X + с ( х _п- х ) ,               (16)

Решение задач (22) и (23) целесообразно проводить последовательно: сначала осуществляя оптимизацию выбора плана НИОКР x _п при

фиксированном в качестве параметра плана П_п по прибыли, а затем выбираем П _f . Это соответствует естественной логике: план НИОКР окажется функцией принимаемых стратегических решений руководства предприятия.

Очевидно, что при фиксированном Пп решение задачи (22) эквивалентно решению задачи maxP{nf > Пп}/Пп = cx ,xп e XJ, (24)

имеющей простой смысл требования выбора плана НИОКР, обеспечивающего при заданном уровне плановой прибыли наибольшую вероятность выполнения плана.

Предположим далее, что каждое из щ ( i = 1, ..., M ) распределено согласно смещенному экспоненциальному закону (6) с параметрами щ , с . Тогда задачи (23) и (24) принимают вид:

max { exp [ S , -стах ( a‘x _п - щ,0 ) J / cx _п =

= ^П п , ^x п ^{e X} } .

Ввиду монотонности экспоненты можно ограничиться решением задачи:

min { S , с , max ( a ' x п — S,° ) / cx п =П п , x п e X } . (26)

В свою очередь, если X – многогранное множество, то задача (26) эквивалентна задаче линейного однопараметрического программирования:

ш(Пп) = min{S,с, Ж / a x п5 щ + ж, i = 1, ..., m, cxп =Пп,xп eX},

которую можно интерпретировать как требование выбора плана, при котором наиболее расходуются негарантированные по уровню ресурсы. Если функция f (П_п) найдена, то оптимальное значение плановой прибыли определяется путем решения задачи (22). Очевидно, она эквивалента следующей:

max |{ ( 1 - а , П п ) e ^{ц (П} " ) ] ,

где максимизация производится на отрезке существования в формуле (27). Решение такой одномерной задачи оптимизации не представляет труда.

Отметим, что решение задачи (24) имеет и самостоятельное значение. Зачастую целесообразно вместо выбора окончательного варианта плана (или наряду с этим вариантом) представлять руководству предприятия график зависимости «прибыль – риск», получающейся непосредственно из задачи (24).

Приведенную схему нетрудно формально перенести и на другие варианты функции эффективности или другие планово-производственные функции.

Опишем подход, связанный с использованием функций эффективности и п.п.ф. в обобщенной форме.

Пусть x _п – плановое решение, x _f – его реализация, ш - случайные факторы («ресурсы»). Ограничения, определяемые свойствами системы, налагаются не на план, а на реализацию. Запишем их в виде:

g ( x f ,щ ) 5 0 .                  ⁽²⁹⁾

Планируемые экономические показатели П_п зависят от планового решения x _п. Фактически достигнутые значения П _f таким же образом зависят от реализации решения x_f :

П п = f ( x п ) , П f = f ( x, ) ,             (30)

где f – некоторые функции.

Эффективность системы зависит от

F = F ( П п , П f ) .                (31)

Планирование преследует своей целью выбор решения x _п , обеспечивающего максимум ожидаемой эффективности. Задача становится определенной, если использована какая-либо гипотеза о связи между решением и его реализацией, выражающейся в задании планово-производственной функции:

x_f = x , ( x „ ,щ ) .                  ⁽³²⁾

Поскольку вектор x_f должен удовлетворять условию (32), то выбор ограничен требованием

g [ x , ( x „ ,щ ) ,щ ]< ^{0               (33)}

при возможных щ- x _п e X , где X - детерминированная область.

Таким образом, задача оптимального планирования сводится к следующей проблеме математического программирования:

max

M щ { F [ ^П п , ^f ( x f ( ^x п ,щ ) ) ] }

---          А ------- = ^П п , x e ^{X f ( x} п )

. (34)

Эта проблема, в частности, может решаться последовательно, поскольку она эквивалентна паре задач:

ш (^П п ) = max , { M щ Ц [ f ( x ) , f ( x f ( x ,щ ) ) / f ( x ) = ^П п , x ^e X ] } ,

^max R f ( ^П п ) ^] ,                         ⁽³⁶⁾

где R _y (•) - любая монотонно возрастающая функция.

Описанная схема, за исключением некоторых частных случаев, несомненно, сложнее в вычислительном отношении, чем формальные способы приведения стохастической задачи к детерминированной, но гибкость процедуры и ее соответствие внутренней сущности задачи планирования НИОКР достаточно привлекательны.

В заключение необходимо обратить внимание на связь схемы оптимизации по функции эффективности с задачей разработки плана НИОКР, обеспечивающей максимум вероятности его выполнения и одновременно удовлетворяющей ограничениям по уровню экономических показателей плана. Именно такой смысл имела задача (24). Но надо иметь ввиду и то, что самая идея выбора плана НИОКР по условию наименьшего риска при заданных ограничениях по экономическим показателям (необязательно по прибыли) достаточно популярна, разумна и конечна. Совершенно независима от приведенных выше рассуждений, касающихся функции эффективности, и п.п.ф. Если при фиксированных го модель имеет линейно-программный вид (то есть A x < x , x e X, щ i - случайные и независимые величины при заданных ограничениях П _i на показатели П _i ( x , l = 1, ..., L )), то задача на максимум риска имеет вид

max <

П i

[ I - w„( a x ) ] П i ( x )

>П i , L = 1, ..., L ,

или, что то же самое,

V [ 1 — W™ ( ax ) ] max ^ >        ——

l     П l(x)

>П i , L = 1, ..., L , -

x e X , (37)

x e X . (38)

Вогнутость целевой функции в задаче (38) для ряда стандартных вероятностей моделей (нормального, равномерного, треугольного распределений) значительно затрудняет

решение задачи ее оптимизации.