Оптимальное распределение ресурсов с использованием динамического программирования

ПОСТАНОВКА ЗАДАЧИ

В общем виде задачи оптимального распределения ресурсов могут быть описаны следующим образом. Имеется некоторое количество ресурсов (материальные, трудовые, финансовые), которые необходимо распределить между различными объектами их использования по отдельным промежуткам планового периода так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения. Показателем эффективности может служить, например, прибыль, себестоимость, суммарные затраты и т. д.

Рассмотрим следующий пример: распределение холдингом специалистов-менеджеров по леспромхозам

Холдинг, включающий целлюлозно-бумажный комбинат и 3 леспромхоза, для повышения эффективности работы леспромхозов решает направить туда 4 менеджеров. Эффективность работы леспромхозов при поступлении в него менеджеров в количестве u повышается в k раз, т. е. представляет собой какую-то функцию fi(u). Все функции fi(n), i = 1, 2, 3 заданы (табл. 1). Как управление холдинга должно распределить менеджеров по леспромхозам, чтобы в итоге максимально повысить эффективности работы леспромхозов?

Таблица 1 Функция эффективности fi(u)

u	f 1 (u)	f 2 (u)	f 3 (u)
1	1.25	1.21	1.18
2	1.08	1.09	1.11
3	-	-	-
4	-	-	-

Холдинг может готовить и посылать в леспромхоз 1 менеджера в год, причем по условию задачи после 4 лет каждый леспромхоз должен получить не менее 1 менеджера. Таким образом, задача разбивается на 4 шага.

Управляемая система в данном случае – менеджеры, которые распределяются. Состояние системы перед каждым шагом характеризуется одним числом – количество еще нераспределенных менеджеров. Шаговым управлением является распределение менеджера u1, u2, ..., u4, в один из 3 леспромхозов. Требуется найти оптимальное управление, т. е. такую последовательность чисел u1*, u2*, ..., u4*, которая дает максимальное повышение эффективности работы леспромхозов в целом, что эквивалентно следующему выражению:

W= W 1 +W 2 +...+W 4 → max.

РЕШЕНИЕ

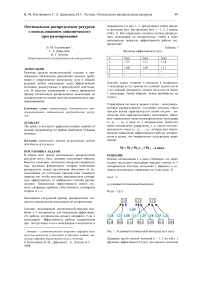
Начнем оптимизацию с 4 шага. Очевидно, что необходимо последнего менеджера передать одному из 3 леспромхозов. Поэтому возможны 3 варианта и условное оптимальное управление на 4 шаге (рис. 4).

u4(s) = s, а условный оптимальный выигрыш

W 4 (s) = f 4 (s).

211      121112

л 1.09

1.18 1.21 1.08 1.11 1.25 1.18 1.25 1.21

/ I :/ I \      \\

210 201   111   021   120   012102

Рис. 1. Условный оптимальный выигрыш на 4 шаге

Задаваясь целой гаммой значений u = 1, 2 по табл. 1 (функция эффективности fi(u)), для каждого значения s определим u4(s) и W4(s). После 4 шага возможны 3 варианта:

• 1)    леспромхоз имеет 2 мене джеров, 2 и 3 леспромхозы имеют по 1 менеджеру 211 ,

• 2)    леспромхоз имеет 2 мене джеров, 1 и 3 леспромхозы имеют по 1 менеджеру 121 ,

• 3)    леспромхоз имеет 2 мене джеров, 1 и 2 леспромхозы имеют по 1 менеджеру 112 .

Рассмотрим 1 вариант 211 .

В это состояние можно перейти из 3 предыдущих:

210 u 41 (2,1,0 → 2,1,1); W 41 (f 3 (1))=1,18;

201 u 42 (2,0,1 → 2,1,1); W 42 (f 2 (1))=1,21;

I 1 11 u 43 (1,1,1 → 2,1,1); W 43 (f 1 (2))=1,08 ;

Рассмотрим 2 вариант 121 .

В это состояние можно перейти из 3 предыдущих:

I 021 u 41 (0,2,1 → 1,2,1); W 41 (f 1 (1))=1,25;

120 u 42 (1,2,0 → 1,2,1); W 42 (f 3 (1))=1,18;

I 111    u 43 (1,1,1 → 1,2,1); W 43 (f 2 (2))=1,09 .

Рассмотрим 3 вариант 112 .

В это состояние можно перейти из 3 предыдущих:

I 012   u 41 (0,1,2 → 1,1,2); W 41 (f 1 (1))=1,25;

102   u 42 (1,0,2 → 1,1,2); W 42 (f 2 (1))=1,21;

111   u 43 (1,1,1 → 1,1,2); W 43 (f 3 (2))=1,11.

Из состояния 111    оптимальным из 3 воз можных шагов будет последний – передача менеджера в 3 леспромхоз. Поэтому 2 других варианта мы исключаем из рассмотрения.

Аналогично рассматриваем 3 шаг.

Оптимизируем 3 шаг, используя соотношение

W i (s) = max {f i (u) * W i+1 (s-u)}

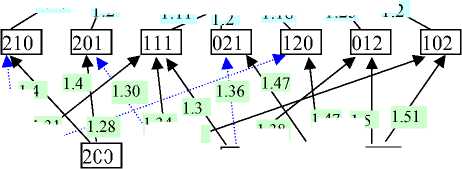
На 3 шаге возможны 7 вариантов, соответствующих распределению 3 менеджеров в 3 леспромхоза (рис. 2).

Рассмотрим 1 вариант 210 .

1.11

1.18    1.25 1.2

1.18 1.2

1.2

1.34

1.3

1.47 1.5

1.38

Рис. 2. Условный оптимальный выигрыш на 3 шаге В это состояние можно перейти из 2 предыдущих:

1.4

1.27 1.31

I 110□    u 31 (1,1,0 → 2,1,0);

W 31 (f 1 (2) f 3 (1)) = 1,08*1.18 = 1.2744;

I 200      u 32 (2,0,0 → 2,1,0);

W 32 (f 2 (1) f 3 (1)) = 1,21*1.18 = 1.4278.

Рассмотрим 2 вариант 201 .

В это состояние можно перейти из 2 предыдущих: I 101      u 31 (1,0,1 → 2,0,1);

W 31 (f 3 (1) f 2 (1)) = 1,18*1.21 = 1. 4278;

200    u 32 (2,0,0 → 2,0,1);

W 32 (f 1 (2) f 2 (1)) = 1,08*1.21 = 1.3068.

Аналогично рассчитываем остальные варианты (рис. 3 и 4).

• 3    вариант:

u 31 (1,1,0 → 1,1,1); W 31 (f 3 (1) f 3 (2)) = 1,18*1.11 = 1.3098 u 32 (1,0,1 → 1,1,1); W 32 (f 2 (1) f 3 (2)) = 1,21*1.11 = 1.3431 u 32 (0,1,1 → 1,1,1); W 32 (f 1 (1) f 3 (2)) = 1,25*1.11 = 1.3875

• 4    вариант:

u 31 (0,1,1 → 0,2,1); W 31 (f 2 (2) f 1 (1)) = 1,09*1.25 = 1.3625 u 32 (0,2,0 → 0,2,1); W 32 (f 3 (1) f 1 (1)) = 1,18*1.25 = 1.475

• 5    вариант:

u 31 (1,1,0 → 1,2,0); W 31 (f 2 (2) f 3 (1)) = 1,09*1.18 = 1.2862 u 32 (0,2,0 → 1,2,0); W 32 (f 1 (1) f 3 (1)) = 1,25*1.18 = 1.475

• 6    вариант:

u 31 (0,1,1 → 0,1,2); W 31 (f 3 (2) f 1 (1)) = 1,11*1.25 = 1.3875 u 32 (0,0,2 → 0,1,2); W 32 (f 2 (1) f 1 (1)) = 1,21*1.25 = 1.5125

• 7    вариант:

u 31 (1,0,1 → 1,0,2); W 31 (f 3 (2) f 2 (1)) = 1,11*1.21= 1.3431; u 32 (0,0,2 → 1,0,2); W 32 (f 1 (1) f 2 (1)) = 1,25*1.21 = 1.5125

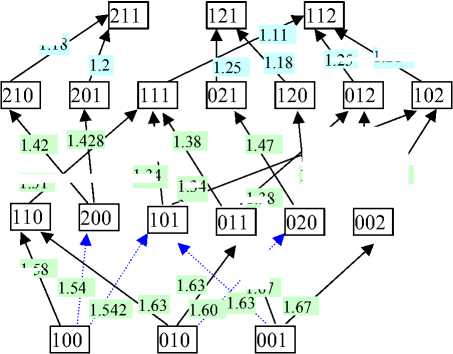
Неоптимальные решения отметим на рисунках пунктирной линией и в дальнейшем не будем их рассматривать .

1.18

1.34

1.58

1.67

1.25 1.21

Рис. 3. Условный оптимальный выигрыш на 2 шаге

1.34

1.31

1.38

1.51	I /
1.475 1                     1	1.51

Таблица 2

s	i	=4	s	i=3
	u 4 (s)	W 4 (s)		u 3 (s)	W 3 (s)
0,0,1	2,1,0	1,18	1,0,0	1,1,0	1,2744
			0,1,0	2,0,0	1,4278
0,1,0	2,0,1	1,21	1,0,0	1,0,1	1,3068
			0,0,1	2,0,0	1,4278
0,0,1	1,1,1	1,11	1,0,0	0,1,1	1,3875
			0,1,0	1,0,1	1,3431
			0,0,1	1,1,0	1,3098
0,1,0	1,1,1	1,09
1,0,0	1,1,1	1,08
1,0,0	0,2,1	1,25	0,1,0	0,1,1	1,3625
			0,0,1	0,2,0	1,475
0,0,1	1,2,0	1,18	0,1,0	1,1,0	1,2862
			1,0,0	0,2,0	1,475
1,0,0	0,1,2	1,25	0,0,1	0,1,1	1,3875
			0,1,0	0,0,2	1,5125
			0,0,1	0,1,1	1,3875
0,1,0	1,0,2	1,21	0,0,1	1,0,1	1,3431
			1,0,0	0,0,2	1,5125

Аналогично рассмотрим первый шаг

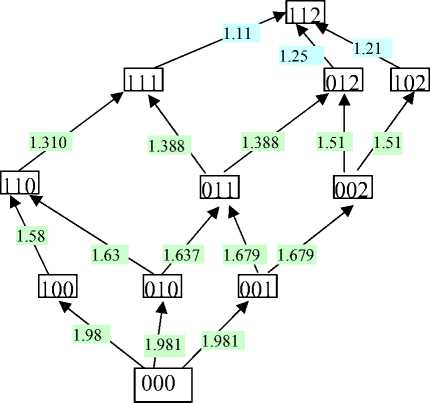
Рис. 4. Условный оптимальный выигрыш на 1 шаге

s	i=2		s	i=1
	u 2 (s)	W 2 (s)		u 1 (s)	W 1 (s)
1,0,0	1,0,0	1,542
1,0,0	1,0,0	1,542
0,0,1	0,1,0	1,6373	0,1,0	0,0,0	1,9811
0,1,0	0,0,1	1,6789	0,0,1	0,0,0	1,9811
0,0,1	1,0,0	1,542
1,0,0	0,0,1	1,6335
0,1,0	1,0,0	1,5849	1,0,0	0,0,0	1,9811
1,0,0	0,1,0	1,6373	0,1,0	0,0,0	1,9811
0,1,0	0,1,0	1,6078
0,1,0	0,1,0	1,6078
0,1,0	0,0,1	1,6789	0,0,1	0,0,0	1,9811
0,0,1	0,0,1	1,6789	0,0,1	0,0,0	1,9811
0,0,1	0,1,0	1,6373	0,1,0	0,0,0	1,9811
0,0,1	1,0,0	1,542
1,0,0	0,0,1	1,6335
0,0,1	0,0,1	1,6789	0,0,1	0,0,0	1,9811

ВЫВОДЫ

В итоге мы пришли к решению задачи.

Как видно из рисунка 4, максимально повысить эффективность лесозаготовительных предприятий можно в 1.981 раза. Причем первичное распределение – в какой именно леспромхоз будет направлен 1 менеджер, значения не имеет. Но все последующие шаги однозначно определены и оптимальное распределение менеджеров в финале таково – в 1 и 2 леспромхоз по одному и в 3 два менеджера.

Полученные числовые данные занесем в таблицу 2.

Цветом в таблице 2 выделены заранее неоптимальные решения, которые в ходе решения задачи отбрасываются.