Оптимальное управление однородной популяцией, находящейся под действием естественного отбора

e-mail: , ;

e-mail: , ;

e-mail: ,

Оптимизация промысла, являясь ключевой задачей математической биологии, не теряет актуальности. Под оптимальной понимается такая доля изъятия из популяции, которая обеспечивает стабильный максимальный равновесный уровень промыслового изъятия при условии невырожде-ния популяции [1, 3], что в теории позволяет балансировать между экономической выгодой и сохранением биоресурсов. Актуальность проблемы возрастает из-за того, что антропогенное воздействие затрагивает жизнедеятельность большинства природных популяций и ставит под угрозу их существование; здесь можно отметить как видоизменение и фрагментацию среды обитания, так и переэксплуатацию отдельных популяций. Это требует уточнения прогнозов динамики популя- ций [5, 7]. Современные методы включают машинное обучение и анализ больших данных для управления промыслом [например, 8-9], однако такие методы более ориентированы на внешние проявления изменения динамики численности популяций и сообществ, но не стремятся выявить внутрипопуляционные процессы, являющиеся причиной этих изменений.

В частности, многие наблюдения подтверждают очевидное предположение, что селективный промысел, меняя условия отбора, приводит к трансформации поведенческих характеристик особей, снижению качества потомства и изменению генофонда популяций [6, 10]. Влияние неселективного промысла на генетический состав популяции не столь очевидно. Данная работа на-

правлена на развитие и дополнение результатов исследований, посвященных анализу эволюционных изменений в однородной популяции, вызванных неселективным оптимальным промыслом [2, 4].

Рассмотрено влияние промысла с постоянной долей изъятия (u) на динамику численности и генетического состава популяции с неперекрыва-ющимися поколениями, подверженной действию плотностно-зависимого естественного отбора:

x n + 1 = w n x n • (1 - u )     _        (1)

qn+i = qn (wAAqn + wAa(1 - qn) /wn ’ где n - это номер поколения, wn = Waaq2 + + 2 WAaqn (1 - qn ) + waa (1 — qn )2 — средняя ПрИСПоСо— бленность популяции в n-м поколении, xn – численность n-ого поколения, измеряемая в относительных единицах; qn – частота аллеля A в n-м поколении, wAA(n), wAa(n), waa(n) – приспособленности генотипов AA, Aa и aa соответственно в n-м поколении; приспособленность зависит от численности популяции линейно: wi j =1 + Rij(1 — x/Ki j). Тогда каждый генотип характеризует его ресурсный (Kij>0) и мальтузианский (Rij>0) параметры.

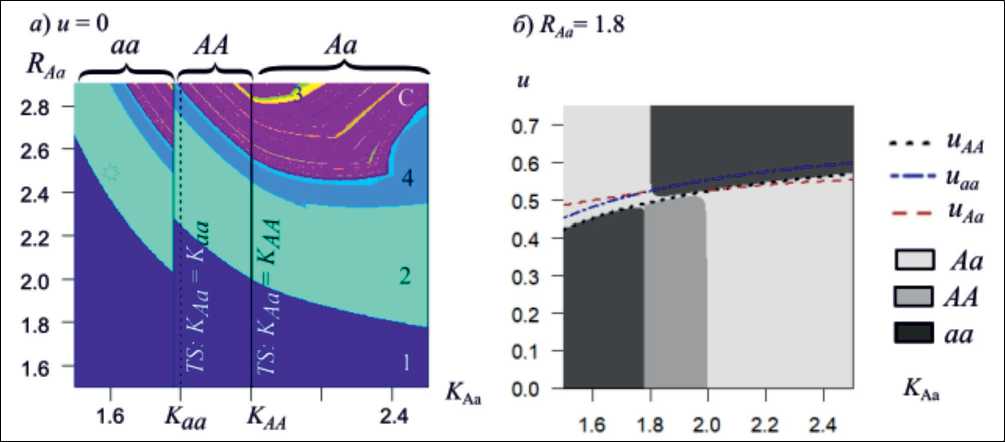
Отметим, что в случае равенства приспо- собленностей всех генотипов: wj =1 + R(1 — x/K) модель (1) представляет собой дискретный аналог модели Ферхюльста: xn+1 = axn(1 — xn/M). Корректность данной модели (x ≥ 0) сохраняется при выполнении следующих условий а а > 2 + 2-^2 [3]. Таким образом, это накладывает на параметры и начальные условия модели (1) следующие ограничения: Rij< 3 и xо

Величина изъятия («урожай») в n-м поколении составляет R_n = u • x_n • wn. В соответствии с концепцией оптимального промысла необходимо определить уровень изъятия из популяции, который обеспечивает стабильный максимальный равновесный промысловый «урожай» при условии невырождения популяции. Система (1) имеет три равновесных решения: два мономорфных ({q=0, x=x 1} и {q = 1, x = x2}) и одно полиморфное {q = q3, x = x₃}. Из первого уравнения системы (1) можно выразить долю изъятия u: u = 1 -1/ w и получить выражение, определяющее объем изъятия в виде: R = x • w • u = x • w — x.

Для того чтобы промысел с постоянной долей изъятия был оптимальным, необходимо вы-

5R полнение условия:

дx x = x

= 0, следовательно,

w + x • w_x'—1 = 0. Далее были определены значения численности и оптимальные доли изъятия в каждом нетривиальном равновесии системы (1), а также проанализированы условия их устойчивости.

Оказалось, что стационарные значения частот аллелей в состояниях, обеспечивающих максимальный уровень изъятия, остаются такими же, как и в случае, когда промысел отсутствует, а равновесные значения численности уменьшаются в два раза. Кроме того, аналитически показано, что при оптимальном изъятии, соответствующем отдельному равновесию, данная неподвижная точка всегда имеет одно собственное значение, не превосходящее единицы по модулю. Второе определяется взаимным расположением приспособленности гетерозиготы и гомозигот при соответствующем данному равновесию уровне численности x_i. Мономорфная стационарная точка оказывается устойчивой, если в данном промысловом равновесии приспособленность соответствующей гомозиготы больше приспособленности гетерозиготы; а полиморфное равновесие оказывается устойчивым, если приспособленность гетерозиготы больше приспособленностей обеих гомозигот при соответствующем промысловом равновесном значении численности популяции. С этим связано проявление эффекта смены типа генетического равновесия в результате неизбирательного промысла (пример на рис. 1). Так полиморфная популяция в результате промысла может утратить своё генетическое разнообразие, а мономорфная, наоборот, сохранить.

Отметим, что каждая из найденных долей изъятия u_ij является оптимальной только для соответствующего ей равновесия. Для других неподвижных точек данный уровень изъятия является произвольным. В результате динамика численности популяции стабилизируется на равновесном уровне, если система оказывается в области притяжения этого равновесия. Поскольку для других двух неподвижных точек системы (1) текущий уровень изъятия в общем случае не удовлетворяет условиям оптимальности при попадании в их область притяжения, динамика численности популяции может продолжить флуктуировать, поскольку одно из собственных чисел текущего равновесия системы (1) может превосходить единицу по модулю. Поэтому вариация начальных условий может менять как результат эволюции промысловой популяции, так и её динамический режим.

Рис. 1. (а) Карта динамических режимов и генетического состояния свободно развивающейся популяции при фиксированном начальном условии х₀ = 0.1, q₀ = 0.1. Числам соответствуют длины циклов, С – хаотическая динамика. Символы аа, АА и Аа обозначают два типа мономорфизма и полиморфизм соответственно; характеризуют генетический состав популяции, который установится в результате отбора. б) Карта генетического состояния популяции, подверженной промыслу с фиксированной долей изъятия (u); кривые u_ij соответствуют оптимальным равновесным долям изъятия

Fig. 1. (a) Map of dynamic modes and genetic states in an unharvested population with fixed initial conditions (x₀= 0.1, q₀ = 0.1). Numbers indicate cycle lengths; C denotes chaotic dynamics. Symbols aa, AA, and Aa represent two monomorphic states and polymorphism, respectively, reflecting the population’s genetic composition established through selection. (b) Genetic state map of a harvested population with fixed removal rate (u). Curves u_ijcorrespond to optimal equilibrium removal rates

Работа выполнена в рамках государственных заданий Института автоматики и процессов управления ДВО РАН (тема № FWFW 2021-0004) и Института комплексного анализа региональных проблем ДВО РАН (тема № FWUG 2024-0005).