Оптимальное управление отбором биомассы из аппарата

Для биотехнологического процесса выращивания дрожжей задачи оптимизации являются особо актуальными, поскольку они характеризуются влиянием множества факторов на скорость развития популяции, сложностью технологического регламента, плохой воспроизводимостью

68                                   БД Agris

данных. Это обусловливает необходимость принятия оптимального решения (в смысле выбранного критерия) при известных начальных условиях и при любом ходе течения процесса.

Постановка задачи оптимального управления отбором биомассы из аппарата

Одной из наиболее актуальных проблем при производстве хлебопекарных дрожжей является задача ведения отбора биомассы из аппарата по ходу процесса культивирования. Возникает необходимость использования текущих данных о процессе и математического описания для нахождения оптимального значения количества отбираемой биомассы из аппарата по ходу культивирования.

Для описания динамики развития популяции дрожжей используется уравнение Ферхюльста –Гаузе [1],     характеризующее их рост:

dx

— = [ ^e - ^e ■ ^x ] • ^x ,             (1)

где ε – коэффициент естественного роста микроорганизмов, ε >0; β – коэффициент, учитывающий внутривидовую конкуренцию микроорганизмов, β >0; x – количество микроорганизмов, t – текущее время.

Необходимо иметь в виду, что:

x(0) = x⁰, x(t) = x⁰, t e [0;t к ], где х⁰ – количество микроорганизмов в аппарате во время отбора; t к – время выращивания микроорганизмов; т. е. необходимо так отбирать биомассу из аппарата, чтобы на всем промежутке времени от 0 до t к , значение концентрации микроорганизмов в аппарате было равно некоторому значению, ниже которого отбор вести нецелесообразно.

В качестве критерия оптимальности выбирается максимальная продуктивность аппарата [2]:

tк

Ф = J c ■ udt + c ■ x(t_K),           (2)

где x – удовлетворяет дифференциальному уравнению:

dx

• — = [ ^e - ^e ■ ^(x - ^u) ] - [ x - u ] - u;      (3)

x(0) = x⁰, x(t) = x⁰, t E ^[ 0;t к ].

Здесь u – количество микроорганизмов, отбираемых из аппарата в каждый момент времени t e [0;t_K ] . В данном случае u является управляющим воздействием и характеризует скорость отбора. Отобранная биомасса не участвует ни в размножении, ни в конкурентном взаимоотношении. с – стоимость единицы объема биомассы. При этом выполняется следующее ограничение:

0 <  u(t) <  x(t).                (4)

Интегральный член в функционале (2) задает общую стоимость биомассы, отобранной из аппарата на всем интервале времени [0, t к ]. Терминальный член в функционале задает общую стоимость биомассы, оставшуюся в аппарате в конечный момент времени t к . Определенный регламентом, интервал времени [0, t к ] считается постоянным.

Задача оптимального управления формулируется следующим образом: на интервале времени от 0 до t к , необходимо найти такое значение u(t), которое обеспечивает максимум Ф в выражении (2) при ограничении в виде (4), при котором концентрация x(t) удовлетворяет дифференциальному уравнению (3).

Определение оптимального значения отбора биомассы из аппарата

Для решения поставленной задачи введем дополнительную переменную х 0 .

dx

• -d⁰- = c - [ e ^- p ■ ⁽x ^{- u)} ] - [ x ^- u ] ; x o (O) = x . (5)

В этом случае задача оптимизации формулируется следующим образом [2,3,4]. Необходимо найти min[-х 0 (t к )] при следующих ограничениях:

dx

• -d¹ = c ^-[ ^{e -} p ■ ⁽x ^{- u)} ] - [ x ^- u ] ,

dx

• — = c - [ e ^- p ■ ⁽x ^{- u)} ] - [ x ^- u ]^- u,    (6)

x0 (0) = x0, x(0) = x0, x(t) = x0, t e[0;tK ], u - x < 0, u > 0.

Функции x и х 0 являются абсолютно непрерывными, u – измеряемая ограниченная функция.

Для решения задачи оптимизации воспользуемся принципом максимума Понтрягина [2, 3]. Определим на конечномерном пространстве х 0 , x, ψ 0 , ψ 1 , u, l I , l 1 , l 2 , функцию Понтрягина H, функцию Гамильтона ^ и концевую функцию L следующим образом:

H(x0 ,x,u,V0 ,Vj ) = -Vg x x{c ■[e — в ■( x — u)] ■ [ x — u ]} —

- V i { c '[ e - в ■ ( x — u ) ]• [ x — u ] - u } ,

^ (x₀,x,u,V g ,V 1 ,l i ,1 2 ) = - V g x x { c ■[ e - в ■ ( x - u ) ]■ [ x - u ] } +

• + v₁ ■ { c ■[ e - в ■ ( x - u ) ]■ [ x - u ] - u } +

+l i ■ [ u — x ] —1 2 ■ u,

L (l„x o (t к )) =- l i ■ x o (t к ).

Из [2,3] следует, что если процесс (х 0 (t),x(t),u(t)) является оптимальным, то он удовлетворяет интегральному принципу максимума. В этом случае на интервале [0,t к ] существуют абсолютно непрерывные функции ψ 0 (t), ψ 1 (t), константа l I >0, интегрируемые функции l 1 (t), l 2 (t), такие, что имеет место:

d^V 1 = V i + l 2 , V i^(t) = ⁰ , t ^{e [0} ;t k^] .   (14)

dt

Воспользовавшись принципом максимума

Понтрягина (11), получим, что если

x >  е • c •

ψ0

,

dx0 _ d^ dx _ d^ =      ,     =      , dt dψ0 dt   dψ1

X o (0) = x⁰, x(0) = x 0 , x(t) = x⁰, t ^{e [} 0;t к^] ;

dV0 = dt

—

d^ dVi dx0   dt

—

d ^ dx ^,

dl

V0 (V = — ,  ,, / dx0(tк)

, A dl2    d«   _

Vi (ti<) = —2—, — = 0.

^1k     dx(t k ), du

Практически при всех t e [0;t_k ] имеет место:

H(x o , x, u, V 0 , V i ) = max ^ (x 0 , x, u, V 0 , V i ),

™ = 0, du ^,

и выполняется условие нормировки:

l i + IIY 0 II + IIY 1 II + III 1 IHII 2 II >  0 .         (13)

Уравнение (7) дает дифференциальную связь поставленной задачи оптимизации, уравнение (8) удовлетворяет сопряженным переменным ψ 0 (t) и ψ 1 (t), выражение (9) – условие локального минимума, а (10) – условие дополнительной нежесткости.

Принцип максимума Понтрягина записывается в виде выражений (11) и (12) [3–10].

Функции ψ 0 (t) и ψ 1 (t) являются абсолютно непрерывными, поскольку, как видно из выражения (7), траектория x(t) никогда не выходит на ограничениеx x(t) =0. Из выражения (8) для dψ сопряженных переменных следует, что —— = 0

^и V o = ^— l i -

Следует отметить, что функции ψ 0 (t) и ψ 1 (t) на всем интервале [0, t к ] одновременно не могут обращаться в ноль, так как из условия d ^

---= 0 следует, что li - I2 =0, при любом t du имеет место x(t) > 0 и из условия дополнительной нежесткости h=12=0 [2,4]. По виду функции ^ d^   d^

получаем: — =---+ Vi +12, и в силу условия dx du

(9) следует, что:

2 • P[c • V 0 + V i ] ψ₁

+ [1 + е] •

,

2 • в[с • V 0 + V i ]

то выражение (11) эквивалентно условию:

dH   d ^

=+ 1₂ — l.

dx du 2   1

Тогда из условия (10) вытекает l 1 – l 2 =0.

В силу этого с учетом справедливости (15) выражение (9) эквивалентно условию (11), и при этом управление u(t) представляется в виде:

u = x —юла... (,6)

2p • [CV 0 + V i ] 2P • [CV 0 + V i ]

Из выражения (13) вытекает, что на интервале [0;t к ] V i < 0. При нарушении неравенства (15) в силу принципа максимума Понтрягина (11) следует, что максимум Η достигается на одном из концов отрезка [0;x]. Следует отметить, что неравенство (15) эквивалентно выражению dH/du < 0. Поскольку d ^ /du = dH /du + 1_i — 1₂ ,то из условия локального минимума (9) следует l i =0, 1 2 ^ 0, что по условию(10) дает u ^ G. Окончательно выражение для управления можно записать в виде:

x—АVi,

2р 2р [V 0 C + V i ]

Vi u = Ии x > 2р+ 2, а - еVi

0, при x <--1--i.

[ ^Р 2р 2р [V 0 C + V i ]

В интегральном принципе максимума 1 x ^ 0. В противном случае это приводит к нарушению условия нормировки (13). Для общности будем полагать l I =1.

Подставляя управление u из (17) в уравнение (6) для траектории x получим:

^{е 2} "        ² V i ^[ V 0 ^{C +} V i ^{] —} V²

x + ,

4в 2в 4в [V 0 C + V i ] 2

dx - е

— = 5 при x >--+ dt р 2в

ψ1

2 ^{е [} V 0 ^{C +} V i ],

ε

^{[е — в} • ^x] • х, при ^x < — +

ψ 1         .

2 ^{е [} V 0 ^{C +} V i ]"

Из уравнения (18) следует, что если ε

x(0) > — , то всюду на интервале [0;t к ] 2β

ε

x(t) > — , к тому же, если при каком либо

Метод определения коэффициентов модели и оптимального значения отбора биомассы из аппарата

Структура макроскопической модели периодического процесса культивирования дрожжей, имеет вид [5]:

t * e [0;t_к ] выполняется неравенство x(t * ) > ^ ,

*ε то на интервале [t ;tк ] имеет место x > —.

Из условия (10) в этом случае следует:

V, (tк) = 0, и неравенство x(0) > — приводит к                             2β к тому, что Vi 0к) = 0 при всех t е [0;tк ].

ε

В случае x(0) < — из условий (10) и (12) 2β вытекает, что V1 ^ 0, траектория x монотонно возрастает одновременно с ψ1 , в момент выхода

' dx "di dS i

, dt

= x ( ц - i ) ,

= ^{- x}q_si ,

i =1,3

где уравнение dX /dt =X( ц - ji ) - модель Ферхюльста – Гаузе (1), записанная в краткой форме; / / - удельная скорость автолиза биомассы, которая вычисляется по формуле:

/ / = К 4 X, где К 4 - константа .

Рассмотрим математическую модель процесса в следующем виде [1,5]:

—

ε

x на уровень сопряженная переменная ψ₁ обращается в ноль и, начиная с этого момента, траектория xизменяется, как и в предыдущем случае.

С учетом этого уравнение (18) примет вид:

dx dt

ε2    ε

4β 2β

ε x, при х > —,

,             2β,

е dX =_e._P„ .- S i‘L₇.- S ²L₇₇— s^ . x --)

dt m K + S <° K₂ + S« K₃ + S 3)

e ■ k₄ ■ x ²⁽¹⁾ - e ■ X ■ x ⁽¹⁾ + (x ⁽¹⁾ - x ^(1-1) );

4               V (i)

e v e          s(1)       s® dt    YX/S1 ' K + S® K2 + S®

(i)

----3      . X - e . m . X ⁽¹⁾ +

K₃ + S 3 ¹ )

ε

^[е - ^в ■ x] ■ х, при х <  2в^.

+ e i. (S 01 - S ( ^-) ) + (S ( ^-) - S ( ^1-1) );

При достаточно большом интервале времени [0;t к ] начиная с некоторого момента тра-

dS 2

^e, = ^-e^ m ■ dt

S₁ (i)              S ( ₂ i)

------— •------— K ₁ + S (¹⁾ K ₂ + s ⁽ ₂ ^-)

S₃ (i)

■ k₃ + S 3 ¹ )

ектория x удовлетворяет неравенству

x > А 2β

X^

, ^(a m2    ^a 02 ) ■ ^S 22

^a 0 ^{2 +}     K 5 + s 2 ^-)

+

и следовательно:

dx ε ² ε

— =1 x .

dt 4β 2β

+ e ■ VF^ 4S 02 - s 2 ^-) ) + (S 2 ¹ ) - s 2 ^1-1) );

В случае стационарного процесса при

dx

— = 0, траектория для dt жением:

x описывается выра-

При

имеет вид:

ε2

ε

x =— + —.

4β 2β

ε этом в силу x > — 2β

ε2

u = —

4β

.

управление

dS 3

^е— = ^e■ U m ■ dt

S₁ (i)              S ( ₂ i)

------— •------— K + s (¹⁾ k₂ + s 2^-)

S ( ₃ i)

■ k₃ + S 3 ¹ )

X ⁽¹⁾ .

α 03

^(a m3    ^a 03 ) ■ S 3

K + S 3 ¹ )

+ e ■ F 4S 03 - S 3 ¹ ) ) + (S 3 ¹ ) - s 3 ^1-1) );

V

F = F 1 + F 2 + F 3 ;

e—= t⁽¹⁾ + t⁽¹⁾ +eV ) ■avx® - dt             в                ⁰

Х ^{(1 - 1)})^⁽¹⁾ - eY ⁽¹⁾ G_B  -AI.

воз

, (24)

где F – объемная скорость подачи питательных веществ; F 1 , F 2 , F 3 – объемные скорости подачи

мелассы, сульфата аммония и диаммонийфосфата соответственно; S 01 , S 02 , S 03 – концентрации сахаров, азота и фосфора в подпитке соответственно, Y Х/ S1 – экономический коэффициент, m – скорость потребления субстрата на поддер-

жание жизнедеятельности, a ₀i и a mi - мини-

мальное и максимальное содержание элемента в биомассе, q_Si – удельная скорость потребления субстрата, θ – время роста микроорганизмов в аппарате, а 0 – коэффициент удельного тепловыделения дрожжей; G воз – массовый расход воздуха, A I - приращение теплосодержания воздуха, Т – температура культуральной среды в аппарате; Т в – температура воды в рубашке аппарата.

Для определения оптимального значения концентрации микроорганизмов и величины оптимального отбора биомассы, необходимо по ходу процесса культивирования определять численные значении коэффициентов модели ε и β . Анализ математической модели, описывающей рост микроорганизмов (24), показывает, что коэффициенты ε и β можно выразить следующим образом:

е = | ц — — + ¹ I , в = K .       (25)

( V о )       ⁴

Расчет значений ε и β необходимо

Система оптимального управления отбором биомассы дрожжей из аппарата

На основе описанной выше методики была разработана автоматическая система управления отбором биомассы дрожжей из аппарата по ходу процесса культивирования [1]. Для исследования системы оптимального управления был проведен машинный эксперимент с использованием опытных данных о почасовом накоплении микроорганизмов, полученных на Воронежском дрожжевом заводе. Данные были получены для 13 часового процесса культивирования с отбором культуральной среды после 6 часа.

Отбор ведется таким образом, что накопление (концентрация дрожжей) X во время отбора остается постоянной при постоянном объеме культуральной среды. То есть забирается объем биомассы, равный объему среды, подаваемой с подпиткой.

Алгоритм исследования системы заключается в следующем. По математической модели (система уравнений (24)) с периодичностью A t =1 ч рассчитываются параметры процесса: Х^р, S 1 , S 2 , S 3 , V и определяются коэффициенты модели ε и β по уравнениям (25). Рассчитывается

производить непосредственно по ходу процесса, используя его математическое описание (систему уравнений (24)).

Отбор биомассы из аппарата начинается при достижении текущей концентрации X

величина ε и сравнивается с введенным экспериментальным значением X (из опытных данных) соответствующим данному моменту времени t. Процедура повторяется до тех пор,

уровня ^ε . Для определения объема био-

массы, отбираемой из аппарата, используется выражение:

— = ц ■ X(i) - K4 ■ X(i) 2 - — ■ X(i) + dt              4 V .

+ 1(Х® - X^{(i - 1)})

При условии, что весь прирост биомассы должен быть отобран во время отбора, можно записать:

пока X не будет больше или равен величине ^ε , или время t не станет больше или равно времени начала регламентного отбора t'.

Рассмотрим оба случая.

1) В случае, если концентрация X больше

или равна величине ^ε , рассчитывается новое

значение

времени

культивирования

t^н = t - кк

t'

- 1

x >

² в V

. Определяется величина

dX u="dt”’

Принимая во внимание нулевые начальные условия, т. е. X^{(i - 1)} = 0, объем отбираемой биомассы определяется как:

¥от =---------F--------

- ц + к₄ ■ X⁽ⁱ⁾ + ¹

X (i)           4           θ

.

управляющего воздействия u из выражения (22) и величина отбираемого объема из выражения (27). Определяется скорость изменения концентрации Х' (по системе уравнений (24)) и для следующего момента времени t =t+ A t предсказывается значение концентрации дрожжей Х^п без учета отбора и значение концентрации X с учетом отбора. Процедура продолжается до тех пор, пока время t не достигнет значения времени культивирования t = t Н .

При этом выводятся значения t, X, V, u.

• 2)    В случае, если концентрация X до момента времени t' (регламентное время отбора) не достигнет уровня ^ε , алгоритм выходит на регламентное определение концентрации: X(t+ ∆ t) =X(t); при этом время культивирования t к остается прежним.

Заключение

Были получены графики почасового изменения концентрации дрожжей и динамика отбора (рисунок 1).

В таблице 1 приведены результаты исследования системы оптимального управления.

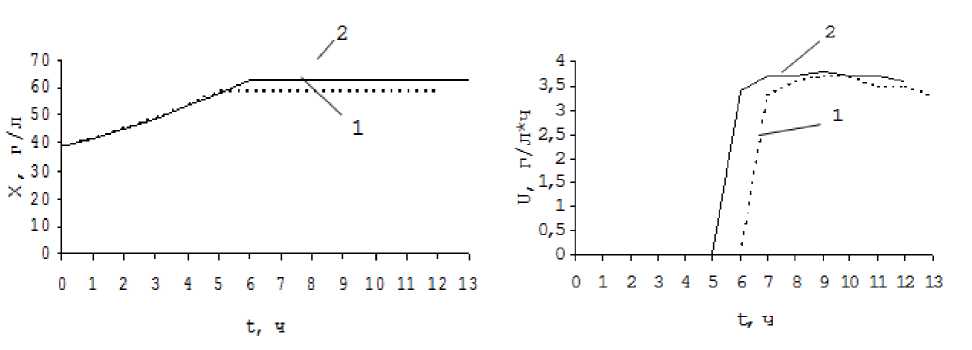
Рисунок 1. Графики почасового изменения концентрации дрожжей X и динамика отбора U – (1 – регламентный; 2 – с учетом оптимального управления)

Figure 1. Hourly charts changes in the concentration of yeast X and the dynamics of selection U (1-regulations; 2 – taking into account optimal control)

Таблица 1

Результаты исследования работы системы оптимального управления (машинный эксперимент)

Table 1

The research results of work of system of optimal control (engine experiment)

Время культивирования t, ч Сultivаtiоn time t, h	Накопление Х, кг/м 3 The accumulation X, kg/m 3	Объем V, м 3 Volume V, m 3	Отбор биомассы u, кг/м 3 ⋅ ч The selection of biomass u, kg/m 3 ⋅ h
0	39	50	0
1	42	52	0
2	45	56	0
3	49	60	0
4	54	64	0
5	59	68	0
6	59	68	3,4
7	59	68	3,7
8	59	68	3,7
9	59	68	3,8
10	59	68	3,7
11	59	68	3,7
12	59	68	3,6

Анализ результатов показывает, что использование такой системы в процессе управления дрожжевым производством позволяет снизить время культивирования на 1 час.

Оптимальная концентрация X =59 кг/м³, t' – время отбора – начало 6 часа; t к =12 ч – время культивирования.