Оптимальное управление процессом культивирования в условиях инфицирования

For cite

Задача управления процессом культи-

вирования микроорганизмов в условиях инфицирования является весьма актуальной. Инфицирование - это обсемененность полезных микроорганизмов (например, дрожжей) “дикими”. Наличие в готовой продукции, кроме полезной культуры, других микроорганизмов, в частности “диких” существенно

dX.

——- = X 1(bx - a 1 X 1 - a 2 X 2) dt dX - b 2 (X 2 - U (t))

I dt

.

Критерий оптимизации имеет вид:

ухудшает качественные показатели конечного продукта. Поэтому борьба с инфекцией путем применения в процессе культивирования антибиотиков требует эффективных алгоритмов управления их подачей. Решению

1 ^T

J ^- _{2 0} L ^x 2 ⁺ qU

dt ^ min ,

задачи управления процессами культивирования микроорганизмов посвящены фундаментальные труды известных ученых: В. В. Кафарова, В. М. Кантере и других. Использование антибиотиков препятствует развитию вредных бактерий и патогенной микрофлоры

и, в частности, не оказывает негативного воздействия на жизнедеятельность дрожжевой клетки и сахара мелассы [5].

В качестве математической модели, описывающей ситуацию конкурентного взаимодействия микроорганизмов из-за потреб-

где q – сравнительная весовая доля указанных затрат.

Необходимо найти вектор оптимальных управлений U(t) для регулирования концентрации посторонней микрофлоры из условия минимума среднеквадратичного критерия (3).

Управление, доставляющее минимум критерию (3) в соответствии с принципом максимума, определяется из условия максимума функции Гамильтона H ( X ₂, y , U ) [2,3,4]:

H - 2( X 2 ² + qU ² ( t )) + ^ ( b 2 X 2 - b 2 U ( t ))  (4)

и вытекающей из нее канонической системы уравнений:

ления одного ресурса, может использоваться система Лотки-Вольтерра [1]. Эта система,

адаптированная для процесса культивирования микроорганизмов, с учетом функции управления U(t) имеет следующий вид [5]:

' dX 2 ”dT -	— - b2X2 -dy   2  2	b 2 U
dy s-------- dt	- ^H -- X2 d X 2      2	- V b г

⁵ H тт к , — ^- qU ^- b 2 ^ . d U

dX 1     л

IT⁼ X ^{1 (} b¹

- a 1 X 1 - a 2 X 2 )

—2- -^- X 2 ( a з X i + a 4 X 2 ) + b 2 ( X 2 ^- U ( t )) I dt

X - X 1 + X 2 и X 2 <<  X 1 , где X ₁ и X ₂ - концентрации полезной популяции и “диких” микроорганизмов; b ₁ , a ₁ , a ₂ , b ₂ , a ₃ , a ₄ - коэффициенты, b 1 и b 2 –

Из последнего уравнения системы (5) находим оптимальное управление:

bi

U ( t ) - -2 • ^ ( t ) .

q

Подставим (6) в первое уравнение системы (5):

удельные скорости прироста соответственно полезных и “диких” микроорганизмов, U(t) – управляющая переменная, регулирующая рост “диких” микроорганизмов .

Ставится задача найти оптимальный закон управления U(t) подачей антимикробных препаратов (неомицина и др.), подавляющих “дикую” микрофлору с целью снижения инфицирования целевого продукта и сокращения расхода сырьевых ресурсов.

Линеаризуем второе уравнение системы (1):

dX ² - b₂X₂

dt ^{2 2}

b ²

- V

q

d v

, dt

- X 2 - V b 2 .

Введем замену переменных: X 2 =x, v =y,

-2

b 2 =a, у - - .

q

Тогда систему уравнений (7) можно переписать в виде:

dx

H = ax — by dy

---= — x — ay.

I dt

а 2 2 =— 2 = — 4 a ² + b .      (14)

Для нахождения матрицы Т условие (11) умножим слева на Т :

Модифицированную сопряженную систему уравнений запишем в матричном виде:

TT ^—1 AT = T Л , AT = T Л .

где матрица

A =

dZ = A • z ,              (9)

dt

Для того, чтобы получить Т такое, чтобы оно диагонализировало матрицу А, необходимо найти решение уравнения (15).

—

I" ¹

—

b

a

вектор-столбец z =

г a	— b J	(t     / 111     112 I	Г 1 11	1 12 J	г 2	0
V— 1	— a J	V 1 21 1 22 J =	V t 21	t 22 J	V 0	2 2
		( a — 2 1 ) t	11 =	bt 12.

Отсюда следует, что при

Решение системы дифференциальных уравнений (9) может быть найдено аналитически следующим образом.

Решение системы (9) имеет вид:

z ( t ) = e^At • C ,             (10)

где С – постоянная интегрирования.

Пусть z=Tv, где Т – неособая матрица перехода к новой

t¹¹ 1: t 12 =

^{— 2} 1 b

⁽ a — 2 ) 1 12 = bt 22 -

a — 2 b

Из чего следует, что a — 2 a + 2

t 12 =1: 1 22 = —- = —— ^- bb

Таким образом, матрица Т имеет вид:

системе координат v.

Тогда (9) перепишется в виде:

T — = ATv .

dt

Последнее выражение умножим на Т ^-1 слева:

T = a — 2

V b

Из выражения (12)

a + 2

b J

T -¹ T — = T⁴ ATv . dt

Обозначим

T ^{— 1} AT = Л ,            (11)

где Л - диагональная матрица собственных значений матрицы А.

Окончательно переходим к уравнению:

— = Л v .               (12)

dt

^Г dv ^J                .

dt J21  0 Yv 1J dv V 0  22 JVv2 J

V dt J

следует, что: v 1 ( t ) = e ^{2 t} • C 1 и v ₂ ( t ) = e ² t

где С 1 и С 2 – константы. Так как

z=Tv, то и вектор-столбец

• C 2 ,

В уравнении (11) две неизвестные матрицы - А и Л . Элементы матрицы Л - собственные значения матрицы А- можно найти

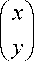
= Tv =

a — 2

V b

a + 2 b

\

( „ 2t_n A e C 1

J

V ^e

— 2 t

C 2 J

из уравнения:

det| A — 2E\ = 0, где Е – единичная диагональная матрица.

Решения (17) запишем в виде:

det

( a — b^

J" ²

V i     a J

Г 1

V 0

Из выражения (13)

2 - a ² — b = 0, поэтому

2 12 = ± 4 a ² + b

= 0.    (13)

следует, что

или

2 1 = 2 = 4 a ² + b ,

' x ( t ) = e ² C 1 + e ^{— 2} C ₂

^a — ² „2 t_r , ^{a + 2} „-2t_r ^-

У ⁽ t ) = —— ^{e C} 1 ⁺ —— ^{e C} 2

I         b             b

' X ₂( t ) = e ^{2 t} C 1 + e ^{— 2 t} C ₂

У ⁽ t ) =

^{( b} 2 ^{— 2 )} q ^b 2 ²

e ² C 1 +

Так как X 2 =x, y =y, b 2 =a,

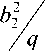
= b ,

^{( b} 2 ^{+ 2 )} q ^b 2 ²

e ²

C 2

При X 2 (0)=X 20 , y ( Т ) = 0 (18) примет вид:

X 20 = C 1

+ C ₂

то согласно (1):

b ₂ U(t ) = C ₂ re ^ b ^{2 -}t - X ₂ ( a 3 X 1 + a 4 X ₂ )     (22)

‘ ^{( b} 2 ^{Я )} q e^c + ⁽ b 2 + ^{X )} q e _„   = о ^.

.       b 22                            b 22

b

Зная U(t) : U ( t ) = — • y ( t ) и y ( t ), из

q

• (18)    получим:

• и ( t ) — b l ( b z X q _C"c 1 +

q     b 2²

и

X ₂ ( t ) = e ^{J b 2 -t} C ₃ - J y re ^{-J b 2 -t} -t ,      (23)

где С 3 – константа.

Из первого уравнения системы (1) (после деления слагаемых на X ₁² ), следует уравнение:

-X 1    b i - a 2 X 2

X ₁ ² dt      X 1

— a 1 — 0 ,

(M X ? ^b 2²

e "  ^{Я Т}С 2 ) =

(b 2 — Я) „XT r , (b 2 + Я) - XT ---------e c +--e c2 • b2          1       b2            2

Целью управления является достижение компромисса между потерями в производстве за счет наличия «диких» микроорганизмов и затратами на их подавление, обусловленное применением антибиотика[5].

Если же использовать допущение [5]:

--2- — b 2 X 2 - r y ( t ) ,         (20)

dt

при

b2T r = 2— 2q ,

которому соответствует:

¹ = e -J b i ^-t * e J ^a 2 ^X 2 ^-t *

X 1                            ,         (24)

[ c ₄ + J a 1 e ^{J b 1 -t} * e ^{—J a 2 X 2 -t} -t ]

где С 4 – константа.

Из (22) с учетом выражений (23) и (24)

видно: во-первых, существенное отличие закона управления, соответствующего допущениям (20) и (21) от (19); во-вторых, отсутствие произвольной функции в уравнении (22), варьируя которой можно удовлетворить какому-либо критерию оптимизации. Таким образом, получен оптимальный закон управления подачей антибиотика (19), позволяющий регулировать концентрацию посторонней микрофлоры в процессе культивирования.