Оптимальное управление решениями начально-конечной задачи для уравнения Буссинеска - Лява

Пусть Q С R n — ограниченная область с границей dQ класса C ” . В цилиндре Q х R рассмотрим yравнение Буссинеска – Лява

(А — A)x tt = а(А — A ' )x t + в (А — A '' )x + и                     (1)

с граничным условием

x(s,t) = 0, (s,t) Е д Q х R.                                 (2)

Уравнение (1) описывает продольные колебания упругого стержня с учетом инерции и при внешней нагрузке, причем отрицательные значения параметра λ не противоречат физическому смыслу задачи.

Данную задачу в подходящих гильбертовых пространствах X и Y , U удается редуцировать к операторно-дифференциальному уравнению соболевского типа,

Ax = B 1 x + B g x + у + Cu,

где операторы A, B i ,B q Е L ( X ; Y ), C Е L ( U ; Y ) , функции и : [0,т) С R + ^ U , у : [0,т) С R ₊ ^ Y (т <  го ).

Рассмотрим начально-конечную задачу [1]

P in (x(0) — x 0 ) = 0, P in (x(0) — x 0 ) = 0;

P fin (x(T ) — x T ) = 0, P fin (x(T ) — x T ) = 0;

здесь P in ( fin ) — некоторые проекторы в пространстве X . Нас будет интересовать задача оптимального управления, которая заключается в отыскании пары (x, и) , где x - решение задачи (3), (4), а и Е U ad - управление, для которого выполняется соотношение

J (x,u)=   min   J (x,u).

(x , u) e X x U ad

А.А. Замышляева, О.Н. Цыпленкова

Здесь J (x, u) - некоторый специальным образом построенный функционал качества, U ad -некоторое замкнутое и выпуклое множество в пространстве управлений U .

Данная работа выполнена в рамках направления, развиваемого Г.А. Свиридюком [2] и его учениками [3, 4]. Мы рассмотрим начально-конечную задачу, которая является естественным обобщением задачи Шоуолтера – Сидорова [5]. Впервые начально-конечная задача была рассмотрена в работах Г.А. Свиридюка и С.А. Загребиной.

1. Полиномиально A-ограниченные пучки операторови проекторы

Пусть X , Y , U - некоторые гильбертовы пространства, операторы A, B 1 ,B o G L ( X ; Y ), C G L ( U ; Y ) . Обозначим через 13 пучок операторов B 1, B o [6]. Множества p ^A (B ) = { p G C : (p 2 A — pB i — B o ) ^{- 1} G L ( Y ; X ) } и c ^A (B ) = C \ p ^A (B ) будем называть соответственно A - резольвентным множеством и A - спектром пучка B . Введем в рассмотрение оператор-функцию комплексной переменной R ^ (B') = (p ² A — pB 1 — B o ) ^{- 1} с областью определения p ^A (B ) , которую назовем A - резольвентой пучка B .

Определение 1. Пучок операторов B^{^} называется полиномиально ограниченным относительно оператора A (или просто полиномиально A -ограниченным), если

3 a G R + V p G C ( | p | >a) ^ (R A (B ) G L ( Y ; X )).

Введем в рассмотрение дополнительное условие

/ RB * ^s O-                    ^(A)

γ где контур y = {p G C : |p| = r > a}.

Лемма 1. Пусть пучок B полиномиально A-ограничен и выполнено (A). Тогда операторы

P = Л [ R A (B)pAdp, Q = Л [ pAR A (B)dp

2пг J ^p                  2пг J ^p

γ

γ

– проекторы в пространствах X и Y соответственно.

Положим X ⁰ = ker P, Y 0 = ker Q, X ¹ = im P, Y 1 = im Q . Из предыдущей леммы следует, что X = X ⁰ ф X ¹ , Y = Y 0 ф Y 1 . Через A k (B l ) обозначим сужение оператора A (B / ) на X k , k = 0,1; l = 0,1.

Теорема 1. Пусть пучок операторов B полиномиально A-ограничен, и выполнено (A). Тогда

• (i)    A^k GL ( X ^k ; Y k ), k = 0,1;

• (ii)    B ^k G L ( X ^k ; Y k ), k = 0,1, l = 0,1;

• (iii)    существует оператор (A ¹ ) ^{- 1} G L ( Y 1 ; X ¹ );

• (iv)    существует оператор (B 0 ) ^{- 1} G L ( Y 0 ; X ⁰ ).

Построим операторы H o = (B ° ) ^{- 1} A ⁰ G L ( X 0 ) и H 1 = (B 0 ) ^{- 1} B ⁰ G L ( X 0 ).

Определение 2. Определим семейство операторов { K _q ¹ , K _q ² } следующим образом:

Kl = H 0 , K 2 = — Hl, K q +1 = K q 2 H 0 , K q ²+1 = K q — K ^ H, q = 1, 2,....

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Определение 3. Точка го называется

• (i)    устранимой особой точкой A-резольвенты пучка B, если K 1 = O, K 2 = O;

• (ii)    полюсом порядка p G N A-резольвенты пучка B, если Ky = O, Ky = O, но K p + 1 = O, K _p ²+i = O;

• (iii)    существенно особой точкой A-резольвенты пучка B, если K k = O при любом k G N.

• 2.    Сильные решения

Определение 4. Если пучок операторов B полиномиально A-ограничен, го - полюс по-

→

—*

рядка p G { 0 } U N A-резольвенты пучка B, то будем называть пучок операторов B (A,p)-ограниченным.

Рассмотрим линейное неоднородное уравнение соболевского типа второго порядка

Ax = B 1 x + B o x + y.

Если пучок B полиномиально A -ограничен, и выполнено условие (А), то существует единственное семейство вырожденных M,N -функций однородного уравнения (6) [7]. Пусть выполнено следующее условие:

A -спектр пучка B a ^A (B) = ct a( B ) U °ia( B ), причем a ^A (B) = 0 , k = 0,1; и существует контур 7 0 C C, ограничивающий область Г о C C такую, что Г о П ■ (B ) = a A (B ), Г о П ^ A (B)= 0 .

(B)

(A o )

Тогда существует оператор

P fin = 2ni 1 ^R A (B )Ad^ G L ( X ).

γ 0

Потребуем выполнение еще одного условия j rA(B)dp = O.

γ 0

Аналогично лемме 1 можно получить следующее утверждение.

Лемма 2. Пусть пучок B полиномиально A-ограничен, и выполнены условия (A), (B), (A o ). Тогда P fin - проектор, причем P fi _n P = PP fin = P fin .

Построим оператор P in = P — P fin G L ( X ) . В силу леммы 2 оператор P in - проектор, причем P fin P in = P in P fin = O . Возьмем произвольные векторы x 0 , x ⁰ , x T , x T G X . Решение x = x(t) уравнения (6) назовем решением начально-конечной задачи для уравнения (6), если оно удовлетворяет условиям (4).

Введем в рассмотрение следующие семейства операторов:

N fin = 2Пг j RA(BW^t G R,

γ 0

M fin = 2- j RA(B )(^A - B i )e^,t G R.

γ 0

А.А. Замышляева, О.Н. Цыпленкова

Лемма 3. Пусть пучок B полиномиально A-ограничен, и выполнены условия (B), (A o ). Тогда

(i) M _f ^• _in и N _f ^• _in – пропагаторы уравнения (6);

•

•

(••)N / ⁰ _in = M fio = O, N fn = M f in = Pf-

Далее, построим семейства операторов M in = M t — M fin , N in = N t —

^N f^tin ^.

Лемма 4. Пусть пучок B полиномиально A-ограничен, и выполнены условия (A), (B), (A o ). Тогда

(i) M _i ^• _n и N _i ^• _n – пропагаторы уравнения (6);

(••)N n = MM O n = O,N n = M in = P in -

Теорема 2. [7] Пусть пучок B (A,p) -ограничен, и выполнены условия (A), (B ), (A o ). Тогда для любых т G R, x k , x T G X , k = 0,1, вектор-функции y = y(t), t G [0, т], такой, что y = (I — Q)y G C ^{p +1} ([0, т]; Y ⁰ ) П C ^p+2 ((0 ,t ]; Y ⁰ ), y ^fin = Q fin y G C ([0 ,t ]; Y ^fin ), y in = Q in y G C ([0,т]; Y in ) существует единственное решение x = x(t) задачи (6), (4), которое к тому же имеет следующий вид:

x(t) = - £ + 2 B) q =0

d ^q

'   y0 (t) + Mfin xT + MinxO + Nfin X1 + Nin x1 + dtq

+ f N (s)ds — £ N*,^ (s)ds.

Определение 5. Вектор-функцию x G H ² ( X ) = { x G L ₂ (0 ,t ; X ) : x G L ₂ (0 ,t ; X ) } назовем сильным решением уравнения (6), если она п. в. на (0,т) обращает его в тождество. Сильное решение x = x(t) уравнения (6) назовем сильным решением задачи (6),(4), если оно удовлетворяет (4).

В силу непрерывности вложения H ² ( X ) ^ C ¹ ([0,т]; X ) наше определение корректно. Термин ≪ сильное решение ≫ введен для того, чтобы отличать решение уравнения (6) в данном смысле от решения (7), которое обычно называют ≪ классическим ≫ . Заметим, что классическое решение (7) является также и сильным решением задачи (6), (4).

Построим пространства Hp+2(Y) = {v G L2(0, т; Y) : v(p+2) g L2(0,t; Y),p G {0}U N}. Пространство Hp+2(Y) — гильбертово со скалярным произведением p+2 „T

[v, w] = ^ J V^wm^^ ^Y dt.

Пусть y G H ^{p +2} ( Y ) . Введем в рассмотрение операторы

A 1 y(t) = — ib K q ² (B 0 ) ^-1 f, (I — QW), q =0

A2y(t) = Jot Nin-syin(s)ds,   A3y(t) = JtT NftTnyfin и функции ki(t) = Mf-nT xT, k3(t) = NfinT xT,

—*

k 2 (t) = M _i ^t _n x ⁰ ₀ , k 4 ^(t) = ^N in ^x 1 -

Лемма 5. Пусть пучок операторов B (A,p)-ограничен, выполнены условия (A), (B), (A 0 ). Тогда

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

• (i)    A i eL( H ^{p +2} ( Y ); H ² ( X ));

• (ii)    при любом x Q E X вектор-функция k i E C ² ([0,т); X );

(in) A 2 EL (H ^{p +2} ( Y ); H ² ( X ));

• (iv)    при любом x ^Q E X вектор-функция k 2 E C ² ([0, т); X );

• (v)    A 3 EL (H ^{p +2} ( Y ); H ² ( X ));

• (vi)    при любом x Q E X вектор-функция к з E C ² ([0,т); X );

• (vii)    при любом x ^Q E X вектор-функция k 4 E C ² ([0,т); X ).

Теорема 3. Пусть пучок операторов B (A, p) -ограничен, p E { 0 } U N, выполнены условия (A), (B), ( A q ). Тогда для любых x k x Q E X , k = 0,1 и y E H ^{p +2} ( Y ) существует единственное сильное решение задачи (4) для уравнения (6).

Доказательство. Подстановка классического решения (7) в уравнение (6) обеспечивает существования сильного решения. Покажем единственность решения задачи (6), (4). Пусть пучок операторов B (A, р) -ограничен, и выполняется условие (A) , тогда в силу теоремы 1. задача (6), (4) распадается на три независимые задачи

HqXq = HX q + xQ + (BQ)-1yQ,(8)

Xfin = S^dcfin + Sfinxfin + (Afin)-1yfin, xfin (т) = xQ ,Xfin(T) = xT,(9)

Xin = sinx in + sQnxin + (Ain)-1yin, xin (0) = xQ, X in(0) = xQ,(10)

где операторы H q = (B Q ) ^{- 1} A ^Q , H = (B Q ) ^{- 1} B Q E L( X ^o) , S fin = (A fin ) ^{- 1} B fin , S f^{i n} = (A fin ) ^{- 1} B fin , S Q n = (A in ) ^{- 1} B Q^ S in = (A in ) ^{- 1} B in E L ( X 1 ) ; вектор-функции x ^Q = (I - P )x , y ^Q = (I - Q)y , x ^{fin ( in )} = P fin ( in ) X , y ^{fin ( in} ) = Q fin ( in ) y ; векторы x ^{fin ( in )} = P fin ( in ) X _k E X ^k , k = 0,1 .

Пусть x и x - два решения задачи (8)-(10). Тогда x = x — x удовлетворяет

AX = BiX + B q X,

Pin(X(0)) = 0, Pin(X(0)) = 0;(11)

P fin (X(T)) = 0, P fin (X(T)) = 0.

Действуя на уравнение (11) последовательно проекторами I — Q и Q fin ( in ) и пользуясь леммой 1, сведем его к эквивалентной системе из двух независимых уравнений

HqXq = HXQ + Xq,(12)

x fin = S fin x fin + S fin x fin X ^fin (T) = 0, X ^fin (T) = 0, X in = S in + S Q n x in , X ⁱⁿ (0) = 0, X in (0) = 0.

Докажем, что x ^Q = x ^Q (t) = 0 при всех t E R . Из (12) следует, что

Q x   1 Y1x + 111x .

Покажем, что xQ = K1 (xQ)(k+1) + Kk(xQ)(k)

при любом k E N. Предположим, что при k = q это верно, и докажем при k = q + 1. В силу (12) (x)(q) = HQ(xQ)(q+2) — H1(xQ)(q+1), поэтому xQ = Kq1(xQ)(q+1) + Kq2(Ho (xQ)(q+2) — H1(xQ )(q+1)) = Kq1+1(xQ)(q+2) + Kq2+1(xQ)(q+1).

Так как ∞ – полюс порядка p A-резольвенты пучка B^ , то в силу определения 3 из (13) при k = p + 1 получаем, что xQ(t) = 0 при всех t E R.□

А.А. Замышляева, О.Н. Цыпленкова

• 3.    Оптимальное управление

Рассмотрим начально-конечную задачу (4) для линейного неоднородного уравнения соболевского типа (3), где функции x , y , u лежат в гильбертовых пространствах X , Y и U соответственно. Операторы A, B 1 , B q E L ( X ; Y ), оператор C E L ( U ; Y ), пучок операторов B (A, p) - ограничен.

Введем в рассмотрение пространство управлений

H ^{p +2} ( U ) = { u e L ₂ (0 ,t ; U ) : u ^{( p +2)} E L ₂ (0 ,t ; U ),p E { 0 } U N } .

Пространство H ^{p +2} ( U ) гильбертово, в силу гильбертовости U , со скалярным произведением

Р ⁺2 т^т /          \

[v,w] = ^2 J \v^№ ,w ⁽ q /и dt-

Выделим в пространстве H ^{p +2} (U) замкнутое и выпуклое подмножество U ad = H dp ⁺² ( U ) - множество допустимых управлений.

Определение 6. Вектор-функцию u E H dp ⁺‘² (U') назовем оптимальным управлением решениями задачи (3), (4), если выполнено соотношение (5).

Нашей целью является доказательство существования единственного управления u E Hp' ² (U), минимизирующего функционал качества

2 _т                     p +2 _т

u ^(q^ dt.

J(x,u) = y / || xw - x ( q ) || ² dt + у / (N q =Q ^J°                       q =Q ^J°

Здесь N _q E L ( U ) , q = 0 , 1 , ... , p + 2 , - самосопряженные и положительно определенные операторы, x(t) - плановое состояние системы.

Теорема 4. Пусть пучок операторов B (A,p) -ограничен, p E { 0 } U N, выполнены условия (A), (B), ( A q ). Тогда для любых x k , x T E X , k = 0,1 и y E H ^{p +2} ( Y ) существует единственное оптимальное управление решениями задачи (4) для уравнения (3).

Доказательство. По теореме 3 при любых y E H ^p+2 ( Y ) , x k , x T E X , k = 0,1 , u E H ^{p +2} ( U ) существует единственное сильное решение x E H ² ( X ) задачи (3), (4), имеющее вид

x(t) = (A i + A 2 + A a )(y + Cu)(t) + k i (t) + k 2 (t) + k a (t) + k 4 (t),            (15)

где операторы A 1 , A ₂ , A 3 и вектор-функции k 1 , k ₂ , k g , k ₄ заданы в лемме 5.

Зафиксируем y E H ^{p +2} ( Y ) , x k , x T E X , k = 0,1 и рассмотрим (15) как отображение D : u ^ x(u). Тогда отображение D : H ^{p +2} ( U ) ^ H ² ( X ) непрерывно. Поэтому функционал качества зависит только от u , т.е. J(x, u) = J(u).

Перепишем функционал качества (14) в виде

J(u) = llx(t,u) - x\H2(X) + [v,uL где v(q)(t) = Nqu(q)(t), q = 0,... ,p + 2. Отсюда

J(u) = n(u, u) - 2A(u) + \x - x(t, 0) \H2(X) , где

^n(u, ^u) = ^(t, ^{u) - x(t}, ⁰⁾ \ H 2 ( X ) ^{+ [v}, ^{u]    -}

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ билинейная непрерывная коэрцитивная форма на Hp+2(U), а

A(u) = (x — x(t, 0), x(t, u) — x(t, 0)^h2(x) - линейная непрерывная на Hp+2(U) форма. Значит, условия теоремы [8, гл. 1] выполнены. □

• 4.    Необходимое условие оптимального управления

Управление u g G H d ⁺² ( U ) оптимально тогда и только тогда, когда

J‘(uo)(u — uo) > 0 Vu G Hd+2(U),(16)

то есть, для функционала (14), выполняется соотношение

(x(t, ug) — X,x(t, u) — x(t,ug)^H2(X) + [ug,u — ug] > 0Vu G Hd+2(U),(17)

где p+2 T

[ug,u — ug] = ^/ Ь%u0q) (t), u(q) (t) — u0q)(t)\ dt(18)

q=o0

билинейная непрерывная коэрцитивная форма на H ^{p +2} ( U ) .

Пусть X * , Y * , U * - сопряженные пространства к X , Y , U соответственно. Введем в рассмотрение изоморфизм

Ли : U ^ U*.(19)

Зафиксируем некоторые векторы (x k ) * , (x k ) * G X * . Операторы A*,B g , B * G L ( Y * ; X * ) .

Введем в рассмотрение А*-резольвентное множество pA*(B*) = {ц g C : (ц2А* — pB* — B0)-1 G L(X*; Y*)} и А*-спектр aA* (B*) = C \ рА* (В*) пучка операторов B*.

Лемма 6. Пусть пространства X и Y гильбертовы. Пучок операторов В (А, р)-ограничен, выполнены условия (A), (B),(A g ) тогда и только тогда, когда пучок операторов В * (А * ,р)- ограничен, и выполнены условия

J RA* (B *w = O;

(А ^* )

(B ^* )

γ ^∗

А * -спектр пучка B * a^A* (13* ) = a A * (B*) U a A * (B * ), причем aA* (B * ) = 0 , k = 0,1; и существует контур y 0 C C, ограничивающий область Г * C C такую, что

Г 0 П a ^A 0 (B * ) = a ^A 0 (B * ), Г О ^Q a ^A * (B * ) = 0 ;

j RA* (B*W = O,                            (А 0 )

γ 0

где y * C C - замкнутый контур, ограничивающий область, содержащую a^A* (И * ), R A * (B * ) = (ц ² А * — pB * — B 0 ) ^{- 1} - А * -резольвента пучка операторов B * .

Операторы

P * =    [ R A (B^^dp, Q * =    [ цА*R A (B*W —

2K'l                                 ^ПЪ

γ ^∗ γ ^∗

А.А. Замышляева, О.Н. Цыпленкова проекторы, P* G L(Y*), Q* 6 L(X*). Положим X*0 = kerQ*, Y*0 = kerP*, X*1 = Im Q*, Y*1 = Im P*.

Теперь определим сопряженное состояние задачи (3), (4) £(t,u) G H2(Y*) как решение уравнения ее                                    •

A*^ = — (B 1 )4 + (B o ) * € + (x(t, u) - x)

на интервале (0; т) , снабженного условиями

P f * in (€(o)) = о, P fin (e(o)) = о, Р^(т)) = 0, Р* п« ( т )) = 0.

Аналогично п. 2 показывается справедливость следующей теоремы

Теорема 5. Пусть пространства X , Y гильбертовы и пучок операторов B (A,p)- ограничен, выполнены условия (A), (B),(A o ). Тогда существует единственное решение ^(t, u) G H ² ( Y * ) задачи (20), (21).

Теорема 6. Пусть пучок операторов B (A, 0)-ограничен. Тогда при любых y G H ² ( Y ) и x G H ² ( X ) оптимальное управление u o G H y ( U ) для задачи (3), (4) харатеризуется соотношениями (20), (21), и выполняется неравенство

(Ли1 C-4(i,uo),u(t) - uo(t)>H2Ш + Х J (Nj?(tW — u*(t)\, > 0 Vu G Hj(U), v ' q=00 '                                    ' U где

x(t,u o ) G H ² ( X ), e(t,u o ) G H ² ( Y * ).

Доказательство. Вектор-функция x(t, u) = x(t, u) — x(t, uo) является решением начально- конечной задачи

P in (x(0)) = 0, P in (x(0)) = 0, P fin (x(T )) = 0, P fin (x(T )) = 0

для уравнения

Ax = B 1 x + B o x + C (u — u o ).

Действуя на данное уравнение последовательно проекторами I — Q и Q fin ( in ), сведем данную задачу к эквивалентной системе

Hox0 = H x0 + x0 + (Bg)-1 (I — Q)C (u — uo),(23)

Afinxfin = Bfinx1 + Bfinx1 + QfinC (u — uo), xfin(T) = 0, x fin(T) = 0,(24)

Ainxin = B1nx1 + B0nx1 + QinC (u — u0), xin(0) = 0, x in(0) = 0.(25)

Здесь H o = (B 0 ) ^{- 1} A o, H 1 = (B o⁰ ) ^{- 1} B 0.

Умножим (24) скалярно на ^ ^fin (t,u o ) и проинтегрируем по интервалу (0,т). Получим

J (Afinxfin(t, u) — Afinxfin(t, uo), ^fin> dt = J [(Bfinxfin(t, u) — Bfin^xfin(t, uo), ^fin\ + о                                                               0

+ ^B fⁱⁿ x ^fin (t, u) — B o fⁱⁿ x ^fin (t,u oM ^fin) + ( Q fin C(u — u oM fin ) ] dt.

Интегрируя по частям левую часть последнего равенства, получим

^J ( A fin x ^fin (t, u) — A ^fin x ^fin (t, u o ),e fin ^ dt = —( A ^fin x ^fin (T, u) — A ^fin x ^fin (T, uo), ^( fin (т) ) + о

+ ( A ^fin x ^fin (0,u) — A ^fin x ^fin (0,u o ),^( ^fin (0) ) + J ( A ^fin x ^fin (t,u) — A ^fin x ^fin (t, u o ), ^ ^fin ) ) dt =

= ^J ( (A ^fin ) * (( fi ⁿ ,x fin (t,u) — x ^fin (t,u ₀ ) ) dt,

о

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ аналогично проинтегрируем по частям выражение

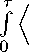
B fⁿ X i™^ u) - B fn X ^fin (t, u o ), ^ fin^ dt = ( B fiⁿ (x ^fin (T, u)

- x fn (T, u o )),f- ⁿ ( t ) )-

-( B {ⁱⁿ (x ^fin (0,u) - x ^fin (0, u o )), 4 ^fin (0) ) - J ( B fiⁿ x ^fin (t,u) - B f^{i n} x ^f^ⁿ (t,u o ),^ f^ ⁿ (t) ) dt = o

= - ^J( X ^fin , (Bf^{i n} ) * 4f^ ⁿ (t) ) dt,

o откуда, применяя условия (21), (22),

^J ( (A ^fin ) * 4' /iⁿ , Xffdt = - ^J( (Bf^{i n} ) * ^ ^fin ,Xf^ ⁿ ) dt + ^J( (B0^{i n} ) * ^ ^fin , X fi ⁿ ) dt+ 0                                  0                               0

τ

+ /(Л — ¹ Сvr : / , (u - u o )W- o

Аналогично найдем

τ  τττ j^(Ain)*^in,xin)dt = - /((B1n)*4in, Xin)dt + /((Bon )*4in, xin dt + /(Л—С*Q*n4in, (u - uo))dt.

o                              o                           o                           o

В силу (A, р) -ограниченности пучка операторов B в случае p = 0 из (23) следует, что

0 = X ^o + (B o ) ^{- 1} (I - Q)C(u - u o ).

τ

0 = j [( (B o^on^o ,X ^o (t,u) o

^{- X}° ^{( t} , ^u o ) ^ ⁺ ( ^Л и 1 ^С * ^{( I - Q)} * ^ ^o j ^{( u - u} o ) ^] ^dt-

Суммируя (26) – (28), будем иметь

ττ

J (A*4, x(t, u) - x(t, uo))dt = J (-(Bi)* 4 + (Bo)*4, x(t, u) - x(t, uo)) + (Л-1С *^, (u - uo))dt. оо

Умножим (20) скалярно на x(t, u) - x(t,u o ) и проинтегрируем по интервалу (0; т)

J(A4, X(t, u) - X(t, uo))dt = J(-(Bi)*4 + (Bo)*4 + (X(t, u) - X), X(t, u) - X(t, uo))dt, о0

тогда неравенство вида (17) можно при произвольном p G N записать в виде

}‘ ( Л _и ¹ С * 4, (u - u o ) ) dt + p £ ^J ( N q u ( ^{q )} (t),u ( ^q ) (t) - u ( ^{q )} (t) \ dt >  0 V u G H d ⁺² ( U ).

o                          q=oo X

• 5.    Уравнение Буссинеска – Лява

Рассмотрим уравнение Буссинеска – Лява (1) с граничными условиями (2). Редуцируя задачу (1), (2) к уравнению (3), положим

X = {x g W2+2(^) : x(s) = 0, s G dQ}, Y = W2(Q), где W2(Q) - пространства Соболева. Операторы A, Bi и Bo зададим формулами A = A - A , B1 = a(A - A’), Bo = в (A - A’’), C = I. При любом l G {0} U N операторы A, B1, Bo G L(X; Y).

А.А. Замышляева, О.Н. Цыпленкова

Обозначим через { A k } (= ст(А)) собственные значения задачи Дирихле для оператора Лапласа А , занумерованные по невозрастанию с учетом кратности. Через { ^ k } обозначим соответствующие ортонормированные (в смысле L ² (Q) ) собственные функции. Поскольку { ^ к } С C ^ (Ю) , то

^2A - дВ1 — Bo = ^[(A — Ak)^2 + a(A - Ak)д + в(Л" - Ak)]   . .■, • > W, k=i где < •, • > - скалярное произведение в L2(Q).

Лемма 7. [9] Пусть выполнено одно из следующих условий:

• (i)    A G а(А);

• (ii)    (A 0 а(А)) Л (A = A ’ );

• (iii)    (A G ^(А)) Л (A = A ‘ ) Л (A = A").

Тогда пучок B полиномиально A -ограничен.

Если выполнены условия (i) или (iii) леммы 7, то имеет место и условие (A) . Если (A G ст(А)) Л (A = A ’ ) , т.е. выполнено условие (ii) леммы 7, условие (A) не выполняется, и мы исключим его из дальнейших рассмотрений.

Л                          "О                                        1 , 2

A -спектр пучка B составляют решения µ _k уравнения

(A - A _k )^ ² + a(A ‘ - A _k )д + e(A" - A _k ) = 0, k G N.                   (29)

Построим проектор P :

• I,    если выполнено (i) ;

  P =

  
  

  I -

  
  

52 G,^ k ) ^ k , если выполнено (iii) .

X = X k

Для построения проектора P fin выберем область Г о С C , содержащую конечное множество точек ^k^ A -спектра ^(B) и такую, что дГ о П ^a A (B) = ® - Как нетрудно видеть, область Г о можно выбрать такой, что дГ о = Y o — контур. Таким образом выполнены условия (B) и (A o ).

Рассмотрим начально-конечную задачу

Е _ui , 2^_ui , 2 < ^ k , x⁽s, ^{0) -} x ^{0 (s)} > ^ k = 0, ^ k = ^ kg

X = X k

E_u 1 . 2-_u1 . 2 < A k , x(s, T) - x T (s) > A k = 0, ^ k = ^ kg

X = X k

E _u 1 - 2 = _u 1 , 2 < A k , x t ⁽s, ^{0) -} x ^{0 (s)} > A k = ⁰, ^ k = ^ kg

X = X k

E„ 1 . 2-, 1,2 < A k , x t (s, T) - x T (s) > A k = 0. ^ k = ^ kg

X = X _k

для уравнения (1) с граничными условиями (2). В силу теоремы 4 имеет место

Теорема 7. При любых a, в G R \ { 0 } и A G R таком, что выполнено условие либо (i), либо (iii) леммы 7, и любых т G R + ,x _k , x T G X , k = 0,1, существует единственное решение задачи оптимального управления (x,y) для уравнения Буссинеска-Лява (1) с условиями (2), (30), минимизирующее функционал (14).

В заключение авторы считают своим приятным долгом выразить искреннюю благодарность профессору Г.А. Свиридюку за постановку задачи и поддержку в работе.