Оптимальное восстановление аналитических функций по их значениям в равномерной сетке на окружности

При г = 0 задача (1) была поставлена и решена в работах [1, 2]. Случай г > О является более сложным и здесь известны результаты лишь при Ц д_ь ... , д„ G (-1,1) (см. [3]) и щ = ... = z_n = 0 (см. [4]).

Данная работа посвящена случаю r = 1, £ Е D и z₃ = т₃ = рДз-^М^ j = 1,... ду 0 <  р < 1. Оптимальный метод восстановления для этого случая приводился в работе [4] без доказательства (при этом для его построения эвристически применялся принцип Лагранжа). Здесь приводится построение оптимального метода восстановления с полным доказательством, используя метод параметризации экстремальной функции, предложенный в работе [3].

Начнем с одного простого вспомогательного результата.

Лемма 1. Пусть комплекснозначная функция УД дифференцируема, в точке До G С как функция вещественных переменных х,у Д = х + ДУ Тогда, если |/(д) имеет экстремум в точке zq , то в этой точке выполняется равенство df —9f

= 0.

+

dz dz

< Пусть /(г) = u(z) + w(^). Тогда из необходимого условия экстремума вытекает,

что в точке ^o	du    du          du    du u—+ v—= 0,   u—+ v—= 0. dx    dx          dy    dy
Отсюда	^ + 7)^ + l(/-7)^ = o, 2        dx            dx ^u + n^ + ^f-n^-». 2        dy   2г        dy

Умножив второе равенство на г и сложив его с первым, будем иметь

/

Эи Эи dx dy

г / ди   ди

2 \ dx   ду

— (1 / ди  ди\   г (ди   ди\\    df  —df _n

+ f ----+ ---1-- = f— + f— = 0

^J \2 \dx  dy)  2\dx  dyjj  ^J dz  ^J dz

Из общих результатов о задачах восстановления (см. [2, 5]) вытекает, что в задаче (1) существует линейный оптимальный метод восстановления

п

Н^^СзМУ

3 = 1

а для погрешности оптимального восстановления имеет место равенство

E^H^z^.. . ,г„) = sup |/(^)|.

fOi ^--^fOn )=о

Теорема 1. Пусть ^ € D, 0 <  р < 1, ^ — е¹^ У^Чь _И _ _ ^, ^ _ ^ _1г Тр_Гд_а

_Flf Н¹ т т I -

(S , -“ ОО , и , . . . , ^тп ) —

а единственным линейным оптимальным методом восстановления является метод

,. п /п— 1        \

/и--Е Е«Т

1 j = l \k = 0       /

f(T3'L

где b₀ = 1,

Pⁿ(q_kf ^k-C^+k) + e(r_k-g_k^ⁿ-^k^ p^k^r_k - p²ⁿ)

n + k        ^2n — кфп + к')

Qk = ^k1 Гк = Цп - k^ ’

к = 1,... , n — 1.

< Напомним, что произведением Бляшке порядка п называется функция вида

п

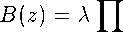
J = 1

1 — a^z

где А = 1, а «7 < 1, 7 = 1,... ,п. В работе [6] было доказано, что если функция /о такова, что /₀(^) = ... = /₀(г„) = 0 и ^ — произведение Бляшке порядка п - 1, то она является экстремальной в задаче (3) при г = 1. Отсюда вытекает, что для г = 1 и ^ = Tj, 7 = 1,... ,П, экстремальной функцией в задаче (3) является функция

-Tl _ f„^ = ---^.

п

Тем самым доказано равенство (4).

Займемся теперь построением оптимального метода. Положим B₀^z) = 1 и

——— ---—, k = 1,... , п - 1,

1 + £_kzB_k_^

где e/J < 1, k = 1,... ,п — 1. Легко убедиться, что B_n_i (е₀ , Л, • • • , Ог-i) € Dⁿ рассмотрим функцию

Для Р =

fp^ = ЕО + j О

Очевидно, что f_P G Н^, и /р₀ = /₀, где Р_о = (—р^п/п, 0,... , 0). Пусть метод (2) является оптимальным в задаче (1) при г = 1. Тогда при всех Р G Dⁿ имеет место неравенство

п

Ы^-'Ес.ы^

Следовательно, модуль функции

1/РоО

уДоЛх,--- ,Gi-i) = fp^ - ^С₃}_Р<т₃^ j=i

в точке Р_о достигает своего максимума. Из леммы 1 вытекает, что в точке Р_о должны выполняться равенства

9 g , -9g

Эе; Эе3

= 0,

7=0,1,... , п — 1.

В силу того, что

Жг-1

= /г-1-1

ЭВ;

9е3

= zⁿ"^j-\ 7 = 1,... ,n-1,

имеем

9/р                  . ₁               aj_P

~—      =----т, 7 = 1, • • • ,п - 1, -— р_р0 п з                      У^о

Аналогичные вычисления дают

9fp          ^j - , Л 8fp р=р0 ^^3                  OEo

Тем самым

^ Р=Р₀ 9д

9^3 р=р₀

и, кроме того,

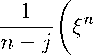
п

Е с-^

fc=l

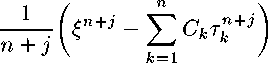
7 = 1,... , п — 1,

п

ЕСг

3 = 1

^- = 1-

>=0.

Учитывая, что т^ = p^u ^ к = 1,... , п, из уравнения (6) будем иметь

CTL TL /                   ^            \      ^ TL /\

L^(^-'3 _pu-3^ckrk3V                    =0, 7 1.,п-1, п — 1 \          ^^      /   П + 1 \          ^^/

J х               fc=i         '           J х               fc=i'

(7) п и ^2 Cj = 1. Положим 3 = 1

п

Ь₃ = ЕС^-                         (8)

к = 1

Тогда п              п

Ескгк3 = ЕскГк"3 =к-3.

Положив a = arg(£ⁿ - pⁿY равенство (7) можно переписать в виде

----_?     _ р-зь_1г_Д = —— ^³ - Р^³ЬД , 7 = 1,... , п - 1. п — 7 \                / п + 7

Введя обозначения

е р’

7 = 1,... , п — 1.

2ia " Т 7 -2-/

Р₃=^е ---7Р Л

77-7

получаем систему b3 -Pjbn-j = тп+з -РзГг \

Взяв из этой системы равенство, сопряженное к равенству, получаемому при j = n — k, и равенство при ; = к, будем иметь

-pkbk + bu_k = т2п"к - ри_ктк, bk - ркЬп-к = тп+к - ркт""к, k = V-- ,п-1.

Отсюда

Ркт""^-1НтЧтп-РкРп-к)

Ьк = --------------:------=------------------•

• 1    -РкРп-к

Это выражение для Ьк легко привести к виду (5). Из равенств (8) и того, что b0 = 1, получаем к=0