Оптимальное восстановление гармонической функции по коэффициентам Фурье

Владимиру Михайловичу Тихомирову к его 70-летию с благодарностью от ученика

Решается задача восстановления в некоторой фиксированной точке единичного круга значения гармонической в круге функции, не превосходящей на этом круге по модулю единицы, по 2n + 1 коэффициенту Фурье граничного значения функции. Также вычисляется точность оптимального восстановления и предъявляется оптимальный метод восстановления для n = 1, 2, 3, 4, а также метод расчета для любого n.

Постановка задачи. Пусть X , Y — нормированные пространства, C ⊂ X — некоторый класс элементов, F — непрерывное отображение из X в Y , x ^∗ — непрерывный функционал на X. (x * , C, F)-задачей восстановления называется проблема восстановления значения h x ^∗ , x i линейного функционала x ^∗ на элементе x, про который известно, что x G C, а также известен вектор F (x), который называется информационным оператором. Любая функция m : F (C) ^ R называется методом восстановления. Требуется найти величину точности оптимального восстановления

E(x*, C, F) = inf sup |hx*, xi — m(F(x))| m x∈C и оптимальный метод восстановления m такой, что sup |hx*, xi — m(F(x)) | = E(x* ,C,F).

x ∈ C

С (x * , C, F )-задачей оптимального восстановления связана следующая экстремальная задача:

hx*, xi ^ max, x G C П ker F называемая ассоцированной задачей. Подробнее о задачах восстановления см. [1].

Формализация задачи. Обозначим через r ^ (D) класс функций двух переменных (р, у) ^ u(p, у), 0 6 р 6 1, — п 6 у 6 п, гармонических внутри единичного круга и ограниченных внутри круга единицей. Наша цель — исследовать (u(r, 0), r ^ (D), Fourn), 0 6 r < 1, где Four n — информационный оператор, сопоставляющий функции u( ^ , • ) коэффициенты Фурье (а о ,..., a n , b i ,..., b n ) функции x0 = u(r, • ), являющейся ограничением на окружность р = r функции u( ^ , • ).

Функции из r ^ (D) представимы в следующем виде:

,    .     1 Г          1 - Р²               _

^{и (} Р, у) = ^    ;—5----л--- fTd, ^{(t) dt},

2п J_{- n} 1 - 2р cos(t - y) + р²

где f (t ) — ««граничное значение» функции, т. е. функция и(р, t) ^ f (t) для почти всех t Е [ — п,п]), удовлетворяющая неравенству || f ( • ) || L ^ ([ _-n ]) 6 1. Подробнее о представимости гармонических функций в таком виде см. [2].

Таким образом, требуется восстановить u(r, 0) функции (р, y) ^ и(р, y), представимой в виде (1), по числам

1 Г X , ao = — J u ^(1, y ^)d y,

a k = — [ u(1,y)cos kydy = — [ f (y)cos kydy ^π - π                   ^π - π

и bk =

— I u(1,y)sin kydy = ^π - π

— Г f (у) sin kydy, 1 6 k 6 n. π - π

Ассоциированная экстремальная задача здесь имеет вид:

^u(r, ⁰⁾ = Л / ^f(tk ¹ r,, ₂ ^dt ^ max,                  ⁽²⁾

2n j_{- n}     1 — 2r cos t + r²

( f (t) cos kt dt = 0, 0 6 k 6 n, ( f (t) sin kt dt = 0, 1 6 k 6 n,

- π - π

где | f ( t ) | 6 1 почти всюду.

Функция P _r (t) = 2 П • - —2———2. называется ядром Пуассона.

Принцип Лагранжа. Задача (2) является задачей выпуклого программирования, у которой функция Лагранжа имеет вид

L = L(f ( • ), A o , P o ,P i , ...,P n ,v-,.. .,V n )

=л a o

1 — r ²

1 — 2r cos t + r ²

n

+ Po + ^^(p k cos kt + V k sin kt)^ f (t) dt.

k =1

Задача (2) является задачей на максимум, поэтому коэффициент A o 6 0. Также можно легко показать, что A o = 0 и мы можем считать, что A o = — 1. Таким образом, функция Лагранжа имеет следующий вид:

L = L(f ( • ), — 1,P o ,P i ,... ,P n , v i ,..., V n )

‘7Г

-

7Г

1       1 — r ²

2n 1 — 2r cos t + r ²

n

+ P o + ^^(P k cos kt + V k sin kt)^ f (t) dt.

k =i

Согласно принципу Лагранжа (см. [1]), если f (•) — решение задачи (2), то существуют такие множители Лагранжа po, Pk, Vk, k = 1,..., n, не равные нулю одновременно, что функция L в точке f(•) достигает своего минимума на множестве BL^([—п,п]), где BL^([—п,п]) — единичный шар в L^([—п, п]). Из ограничений (3) следует, что f (•) Е Tn⊥ , где Tn — пространство тригонометрических полиномов степени n. Отсюда следует, согласно критерию наилучшего приближения в Lp (см. [1]), что n

P o +    ( P _k cos kt + V _k sin kt )

k=i является полиномом наилучшего приближения функции Pr (t) = ^П • __L-T—r2 подпространством Tn тригонометрических полиномов степени n в метрике Li([—п,п]).

Таким образом, для решения нашей задачи нам нужно найти тригонометрический полином наилучшего приближения функции P r (t) в метрике L i ([ — п, п]) и тогда

E(u(r, 0), r^(D), Fourn) = d(Pr(•), Tn, Li([—п, п])), где E(u(r, 0), r^(D), Fourn) — погрешность восстановления функции u(r, •) по 2n + 1 коэффициенту Фурье граничной функции, а d(Pr(•), Tn, Li([-п, п])) — расстояние от функции Pr (•) до пространства тригонометрических полиномов степени n в метрике L1([-п,п])1.

Нахождение полинома наилучшего приближения. Так как функция P r (t) четная относительно t, полином наилучшего приближения должен быть четным, а, следовательно, мы можем считать, что все коэффициенты при синусах в полиноме наилучшего приближения этой функции равны нулю, т. е. V k = 0, к = 1,... n. Значит полином наилучшего приближения функции

P (t) =

2п

1 — r ²

1 — 2r cos t + r ²

имеет вид

n

T nr (t) = E ^ k cos kt, k =0

где ^ k = ^ knr , т. е. ^ k еще зависит от n и r.

Рассмотрим выражение вида

1        1 — r ^{2          n}

^A(t) = P r ^{(t) —} T nr ^(t) = — • 1 — 2r cos t ₊ r 2 ^— E ' k ^{cos kt} k =0

и докажем, что A(t) может равняться нулю не более чем в n + 1 точке отрезка [0,п]. Используя представление k cos kt = У^ aj cosj t j=i и выражение (4), получаем представление A(t) в виде

1          1 — г²           ”

^A(t) = 2 п • 1 — 2r cos t + r 2 ^— X ^e k ^cos t^- k =0

Производя замену z = cos t, приходим к равенству

1       1 — r ²

A("ccos     2 ■■ • 1 — 2' + r2 — S ekz - k=0

Продифференцировав n + 1 раз по z, получаем

(1 1 — r2 — X e zk!(n+1) = j^—N^+^d—r!!-у 2п 1 — 2rz + r2 k=0 k у        2п(1 — 2rz + r2)n+2 , а это выражение вообще не имеет нулей на отрезке [0,п], следовательно, по теореме Ролля заключаем, что функция -П • у--—+ r2 — Pn=o вкzk не может иметь более чем n + 1 нуля на отрезке [0, п]. Учитывая строгую монотонность функции t = arccos z, делаем вывод, что выражение

1          1 — r2”

At • 1 — 2r cost + r- -‘ k=0

также не может иметь более чем n + 1 нуля на отрезке [0, п].

Таким образом, если мы найдем такой полином T nr (t) = ^2n=o Ц к cos kt, что

A(tj) = Pr(tj) — Tnr(tj) = 0 только в n + 1 точках to, ti,..., tn,(5)

то, согласно критерию элемента наилучшего приближения в L 1 в случае приближения подпространством (см. [3]), следует, что T nr (t) является полиномом наилучшего приближения для функции P r (t) = - П • ——АО—_ подпространстом T n в метрике L 1 ([—п, п]).

Рассмотрим тригонометрический полином T _nr (t) такой, что

P r (t j ) = T nr (t j )

во всех различных точках нулей функции cos nt на отрезке [0,п]. Этот полином удо- влетворяет условию (5) и поэтому является полиномом наилучшего приближения для функции Pr (t). Заметим, что функция cos nt имеет ровно n + 1 корень tj на отрезке

[0, п], где

π       πj

^tj = - 2(n + 1) ⁺ n+1, j = ^0,‘“^,n-

Для того чтобы построить такой полином нужно решить систему из n + 1 линейного уравнения относительно µ 0 , µ 1 , . . . , µ _n- 1 , µ _n ¹ :

Ц o + Ц 1 cos t o + Ц - cos2t o +----- + Ц п — cos(n — 1)t o + Ц п cos nto = b r 0

<   Цо + Ц1 cos t j + ц ₂ cos 2t j + • • • + ц _{п- 1} cos(n — 1)t j + ц _п cos nt j  =   b rj       (7)

Решение этой системы в аналитическом виде мы выписывать не будем, но объясним как решать эту систему линейных уравнений численно для любого натурального n > 1.

/ b r 0 \ b r 1

Представим систему (7) в виде Апц = br, где ц = (цo,Ц1, ...,Цп) и br brn

Матрица A _n этой системы имеет вид

A n

/ 1 cos t o cos 2t o ... cos nto \ 1 cos t1 cos 2t 1 ... cos n t1

.                         .                                      .                            ..

..      .     ..

..      .     .

\ 1 cos t _n cos2t _n ... cos nt n J

Определитель этой матрицы не равен нулю, для каждого фиксированного r ∈ (0, 1) и n >  1 все элементы матрицы A n и элементы столбца b r определены, поэтому решением системы уравнений (7) является

µ = ( µ 0 , µ 1 , . . . ,µ n ) = A _n ^-1 b r .

Тем самым мы показали как рассчитать все ( µ 0 , µ 1 , . . . , µ n ), которые являются коэффициентами тригонометрического полинома наилучшего приближения T _nr ( t ) = P n =0 ^ k cos kt Для функции 2 п • i_-2T ^— o_{S t} + _r 2 ■ Этот способ мы использовали для расчета численных значений коэффициентов µ k для определенных n и r .

Оптимальный метод восстановления. Задачу (2) можно рассматривать как ассоциированную с задачей оптимального восстановления функционала

π2 f(·)→21π -πf(t)1-21rcosrt+ на множестве f(·) ∈ BL1 ([-π, π]) по информации f (•) ^ (— I f (t) dt, — I f (t) cos ktdt, — I f (t) sin ktdt, 1 6 k 6 n). 2π -π        π -π              π -π

Из теоремы о двойственности для задач восстановления (см. [1]) вытекает, что оптимальный метод для задачи (1) имеет вид

1 ^π            1 - r ^{2             n}

u(r,0)=2π -πf(t)1-2rcost+r2dt≈k=0µkak, и точность оптимального восстановления равна

π

E nr = E u ( r, 0) , Γ ∞ ( D ) , Four n

-

π

1       1 - r ²

2 π 1 - 2 r cos t + r ²

— T nr

dt.

Расчет оптимального метода и погрешности оптимального восстановления. Все расчеты оптимального метода и погрешности оптимального восстановления производились с помощью математического программного обеспечения Mathematica 4.0, где мы применяли метод (9), описанный выше. Далее приведены расчеты для n = 1 , 2 , 3 , 4 при r = ¹ ₄ , ¹ ₂ , ³ ₄ . ¹

Случай n = 1. При n = 1 мы интерполируем в точках t1 = ( 14π, 34π), вектор b1 = (21π · 1-√1-2rr2+r2, 21π · 1+ 1√-2rr2+r2), а матрица A1 имеет вид

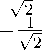
A 1 =

Тогда используя формулу (8), получаем, что µ = ( µ 01 _r , µ 11 _r ) = A ₁ ^-1 b 1 . Для r = ¹ ₄ , ¹ ₂ , ³ ₄ получаем соответственно, что

E ₁ 1 ₄ = 0 . 07947409722 ,  µ ₀₁ 1 ₄ = 0 . 1579163832 ,  µ ₁₁ 1 ₄ = 0 . 07431359201;

E ₁ 1 = 0 . 3119165215 ,    µ ₀₁ 1 = 0 . 1404308321 ,  µ ₁₁ 1 = 0 . 1123446656;

E 3 = 0 . 6523945232 ,   µ 3 = 0 . 08264722565 ,  µ 3 = 0 . 07934133662 .

1 ₄                                01 ₄                               11 ₄

Случай n = 2. При n = 2 мы интерполируем в точках t2 = 16 π, 12 π, 56 π , вектор b2 =   1

2π

1 - r ²       1

1 - ^√3r + r ^{2 ,} 2π

1 - r ² 1

1 + r ^{2 ,} 2π

1 — r²    \

1 + ^√3r + r ^{2 ,}

а матрица A 2 имеет вид

/ 1    У(3)i

A2 =   1    0    —1.

1 -√2(3)1

Тогда, аналогично, для r = ¹ ₄ , ¹ ₂ , ³ ₄ получаем соответственно, что

E ₂ 1 ₄ = 0.01989274912, µ ₀₂ 1 ₄ = 0.1590772497, µ ₁₂ 1 ₄ = 0.07924727455, µ ₂₂ 1 ₄ = 0.05876490209;

E ₂ 1 ₂ = 0.1583336966,  µ ₀₂ 1 ₂ = 0.1542578679, µ ₁₂ 1 ₂ = 0.1469122552,  µ ₂₂ 1 ₂ = 0.3692307696;

E ₂ 3 ₄ = 0.5083036709,  µ ₀₂ 3 ₄ = 0.1110621127, µ ₁₂ 3 ₄ = 0.1385390181,  µ ₂₂ 3 ₄ = 0.06649872866.

Случай n = 3. При n = 3 мы интерполируем в точках t3 = 18π, 38π, 58π, 78π , вектор b =    1  ·       1-r2         1  ·       1-r2         1  ·       1-r2         1

1 - r ²

1+2 r cos ¹ π + r ² 8

3      2π 1-2r cos 18 π+r2 , 2π 1-2r cos 38 π+r2 , 2π 1+2r cos 38 π+r2 , 2π а матрица A3 имеет вид

		1	cos 1 π 8	1 √ 2	cos 3 π 8
A 3 =		1 1	3 cos 8 π - cos 3 π 8	1 2 1 ^^^^^^^^^^^^^^^^^^^^^^^^.   ^^^^^^^^^^^^^^^B 2	- cos 1 8 π cos 1 π 8
	I	1	- cos 1 8 π	1 √ 2	- cos 8 π

Тогда, аналогично, для r = ¹ ₄ , ¹ ₂ , ³ ₄ получаем соответственно, что

E ₃ 1 ₄ = 0.004973566675, µ ₀₃ 1 ₄ = 0.1591500860, µ ₁₃ 1 ₄ = 0.07955682940,

µ ₂₃ 1 ₄ = 0.01981635313, µ ₃₃ 1 ₄ = 0.004662671321;

E ₃ 1 ₂ = 0.07947409722, µ ₀₃ 1 ₂ = 0.1579163832, µ ₁₃ 1 ₂ = 0.1560585433,

µ ₂₃ 1 ₂ = 0.07431359205, µ ₃₃ 1 ₂ = 0.02972543681;

E ₃ 3 ₄ = 0.3901710410, µ ₀₃ 3 ₄ = 0.1301879796, µ ₁₃ 3 ₄ = 0.1783845740,

µ ₂₃ 3 ₄ = 0.1112585701, µ ₃₃ 3 ₄ = 0.05340411362.

Случай n = 4 . При n = 4 мы можем аналогично вычислить точки интерполяции t 4 , вектор b 4 , а также матрицу A 4 , но в данной статье мы приведем только вычисленные µ k 4 r для r = ¹ ₄ , ¹ ₂ , ³ ₄

E ₄ 1 ₄ = 0.001243397598, µ ₀₄ 1 ₄ = 0.1591546395, µ ₁₄ 1 ₄ = 0.0795761813,

µ ₂₄ 1 ₄ = 0.01988949187, µ ₃₄ 1 ₄ = 0.004954159145, µ ₄₄ 1 ₄ = 0.001165684519;

E ₄ 1 ₂ = 0.03977579129, µ ₀₄ 1 ₂ = 0.1588443968, µ ₁₄ 1 ₂ = 0.1583785776,

µ ₂₄ 1 ₂ = 0.07825765008, µ ₃₄ 1 ₂ = 0.03726554766, µ ₄₄ 1 ₂ = 0.01490621911;

E 3 = 0.2966583314, µ 3 = 0.1421854074, µ 3 = 0.2033792176,

4 ₄                           04 ₄                           14 ₄

µ ₂₄ 3 ₄ = 0.1393358858, µ ₃₄ 3 ₄ = 0.08690387937, µ ₄₄ 3 ₄ = 0.04171386190.

Эта работа является первым шагом в исследовании задач восстановления значений гармонических функций на многомерных шарах.