Оптимальное восстановление производных на соболевских классах
Автор: Магарил-Ильяев Георгий Георгиевич, Осипенко Константин Юрьевич
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 1 т.5, 2003 года.
Бесплатный доступ
Рассматривается задача оптимального восстановления производных функций из соболевских классов на \Bbb R^d по неточной инфориации об их преобразовании Фурье. Доказано, что существует область \Omega_0\subset\Bbb R^d такая, что информация о преобразовании Фурье в любой области содержащей \Omega_0 не ведет к уменьшению оптимальной погрешности восстановления.
Короткий адрес: https://sciup.org/14318071
IDR: 14318071 | УДК: 517.51
Текст научной статьи Оптимальное восстановление производных на соболевских классах
Рассматривается задача, оптимального восстановления производных функций из Соболевских классов на. Ж6* по неточной информации об их преобразовании Фурье. Доказано, что существует область fi0 С Ж6* такая, что информация о преобразовании Фурье в любой области, содержащей По, не ведет к уменьшению оптимальной погрешности восстановления.
В данной работе рассматривается задача оптимального восстановления производных функций из Соболевских классов на IRd по информации о преобразовании Фурье самих функций, заданном приближенно. Перед постановкой задачи приведем некоторые определения. Пусть a = (ад,... , аД G Ж^. Для функции ж(-) G ГДЖ1') через Р“ж(-) будем обозначать производную порядка а по Вейлю, определяемую равенством
Dax^ = —i-y I(ДДЕх^е1^ dT, где
(гтД = (zti)"1 ... (гтдД4, Д,^ = тД1 + ... + Tdtd, а Еж(-) — преобразование Фурье функции ж(-). Соболевское пространство 'НДЖ1') определяется как совокупность функций ж(-) G ГДЖД таких, что
/ \ 1/2
h(')h;(Bd) = I ^р ] (! + WY |Еж(/)|2йИ < оо,
\ кд )
где ||t||2 = t2 + ... + t^. Соответствующим Соболевским классом назовем множество
Я2Д^) = {жОе?Д(^):||жО||^(К^
Задача оптимального восстановления оператора Da на классе НДЖ1') по преобразованию Фурье функции ж(-) G НДЖ1'), заданному с погрешностью б > 0 в метрике ГДЖ1), ставится следующим образом. Мы считаем, что для каждой функции ж(-) G НДЖ1') нам известна функция уД G ГДЖД такая, что
\\Р$И - УИ\\ьдж») С 5.
В качестве методов восстановления будем рассматривать всевозможные операторы р;Ь2^Жа>) —> Ь2^Жау Погрешностью данного метода у назовем величину
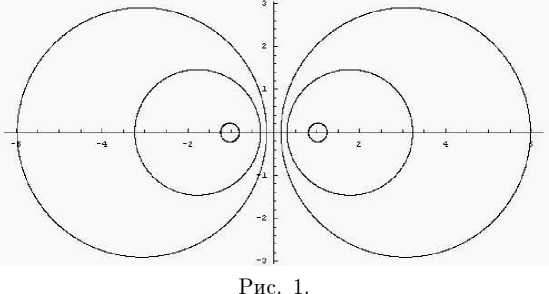
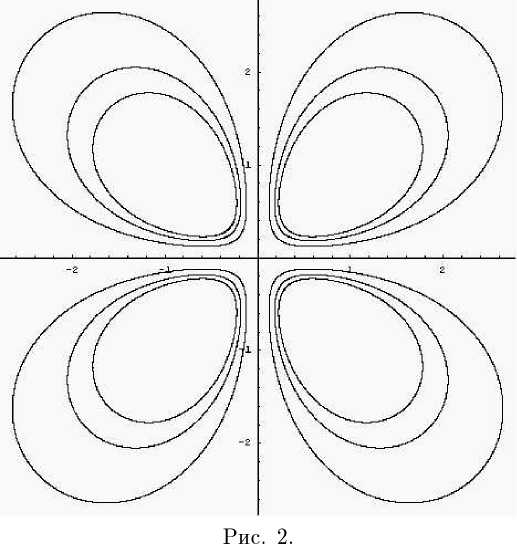
e(D“,H^,5,^ = sup ^“x^-^HW^w д^ПцО, yeM Нас будет интересовать погрешность оптимального восстановления, определяемая равенством Е^П“,Н^Жауб^ = inf е^Щ^ЛрУ (1) у:£2^Н-ЫкА а также метод, на котором достигается нижняя грань, называемый оптимальным методом восстановления. Впервые задача оптимального восстановления для функционалов по конечномерной информации была поставлена С. А. Смоляком [1]. Впоследствии эта постановка обобщалась и развивалась в разных направлениях (см. [2-6]). Подход к задачам восстановления, основанный на общих принципах теории экстремума, который мы здесь также используем, развивался в работах [7-10]. В данной работе мы сначала решаем задачу (1), а затем обсуждаем некоторый эффект, связанный с тем, что знание преобразования Фурье лишь на некотором подмножестве Rd обеспечивает ту же погрешность оптимального восстановления, что и на всем пространстве. Теорема 1. Пусть а = («1,... , а^ G R^, а ^ 0, г > 1 и а = Хд = 1 aj < r-Положим Л (2тг)^/2’ л° ( г / ’ Р ' Тогда, если 0 < б < (2тг)с,/2Ао, то а метод E(,D“,H^Vy6^ (1 - Д2Л' тО"/2 \ D“^^i- Rd 1 + ,И?\„ . (1 + МТ /■(△о7 - А2/’’) (1т является оптимальным. Если б > (2тг)сг72До, то Е^Н^^ = ^т - а^'2, а Dax^ ~ 0 — оптимальный метод. < Нетрудно показать, что имеет место следующее неравенство E(D“,HT2^ay5^ sup \\D“x^\\L2W. II FA ') II l2 (R^) ^^ Действительно, для любого метода у при всех ж(-) G ЯДКД таких, что ||Еж(-) Ц^^д) С 5 (учитывая, что -ж(-) Е Щ^Жа^, имеем 2\\D“aO\L2W С \\П“х^-(р^^\\ьд^ + || - D“x^ - y(0)(-)||L2(Kd) С 2e(D“^(Rd),M- Следовательно, для любого метода у е(Я“,ЯДКДД,у) > sup \\D“x^\\L2W.. 1ЯЯ) L2 (ntd ) ^ откуда сразу же вытекает оценка (2). Экстремальная задача в правой части неравенства (2) может быть записана в виде (для удобства мы ищем квадрат значения этой задачи) P^UIlLfRdj ^ max, ||M')llL2(Rd) ^ 5, ||ж(-)||Иг(к^) ^ 1. (3) В силу равенства Парсеваля 1И-)11^) = (^)Л^ж(Д|2^ полагая Д.) = (2тг)->ж(.)|2, задача (3) в образах Фурье запишется в виде j \t\2au(t) dt —> max, Rd ju(t)dt^A2, I (1 + ||t||2)ru(t)^ C 1, u(t) > 0 п. в., (4) Rd Rd где l|2a = H|2ai . ..|Д|2ад. Можно показать, что в этой задаче нет решения. Поэтому расширим ее, заменяя функции положительными мерами. Итак, рассмотрим следующую задачу j \t\2a dp^ —> max, Rd j dp^< A2, Rd У (i + ||t||2)r^(t)^i, dpl^O. Rd Это выпуклая задача. Ее функция Лагранжа имеет вид ОДДДАщА^Аг) У (^оД2“ + Ai + Аг (1 + ||^||2) ) dp(t\ Rd Если dp^-) — решение задачи (5), то согласно теореме Куна — Таккера (см., например, [8]) найдутся такие Aq СО, Ai, А2 ^ 0, не равные нулю одновременно, что и Кроме того, если для допустимой в (5) меры dp^ выполняются условия (6) и (7) с Aq< 0 и Ai,A2 ^ 0, то фи(-) — решение задачи (5). Действительно, для любой допустимой меры dp^ имеем (используя последовательно допустимость этой меры и неотрицательность Aj, г = 1,2, условие (6) и условие (7)) Ло/ Rd t|2adp^ > Ao j |t|2adp^ + x3j dp^ - A2 Kd NRd ) + Аг у (1 + ||t||2)’ dp^ - 1 > Aq у |t|2adp^ Wd ) Kd + Ai 1 / dp,^ — A 1 + A2 1 / (1 + II^H ) dp^t) — 1 = Aq У |t|2“ dp(t\ Rd Предъявим dp(-) ^ 0 и Aq< О, Ai, Аг ^ 0, для которых будут справедливы равенства (6) и (7). Введем следующие обозначения А = min(A2, Aq), I А-Or _ i 1/2 ] Т tj = \ ----------а/, 7 = 1,..., а, t = (Н,... ,td) и положим Aq = — 1, - pIA"yIt -i д-'л'-'/'' Ao = --------------;--------- и dp^ = AS^—t), где Д-) —дельта-функция в нуле. Легко видеть, что Ai Д О (Ai = О, когда А = Aq) и Аг > 0. Непосредственная проверка показывает, что мера dp^ допустима и справедливы равенства (7). Для доказательства равенства (6) достаточно доказать, что функция G(t) — — Д2“ + Ai + Аг (1 + ||£||2) неотрицательна и в точке t обращается в ноль. Предположим сначала, что «j >0,7 = 1,... , d. Сделаем замену переменных Д = 2 In\tj , j = 1,... , d, в функции \t\-2aG^, \t\ > 0. Тогда получим функцию F^ = -1 + е"^ (М + А2 (1 + е^ + ... + e^f) , £ = (^,... , ^). Нетрудно убедиться, что эта функция выпукла, F^ = 0, где £ = (£i,... , ^), £7 = 2 In \tj\, 7 = 1,... , d, и, кроме того, градиент этой функции в точке £ равен нулю. Это означает, что F^ ^ 0 при всех £ G Rd. Отсюда, возвращаясь к старым переменным, получаем, что 0(1) ^ 0 для всех t G Rd и G(t) = 0. Если среди ctj есть нули, то аналогичные рассуждения приводят к тому же выводу для функции О( ), зависящей лишь от тех переменных, для которых соответствующие ctj > 0. Добавляя оставшиеся переменные в функцию G^ легко убедиться, что полученная функция по-прежнему останется неотрицательной, а 0(1) = 0. Тем самым имеет место равенство (6), и значит, dp(t) — решение задачи (5). Для ее значения имеем R := J |1|2“ ^(1) кд ^Д2(1-^/»-) (1 - Д2Лу , 5< ^тгД^До, ^-^-у 5 > (27г)й/2Д0. Эта величина дает оценку снизу для значения задачи (4), а, следовательно, и для квадрата значения задачи (3). Но эта оценка точна, так как можно выбрать последовательность допустимых в (3) функций ж„(-) G £2(Rd) таких, что ^л-Д^жД-)!2 —> АД- — 1) при п —> оо. Итак, получена оценка снизу к^пун^уй) > Vr. Для получения оценки сверху рассмотрим экстремальную задачу llsa^(-)llL2(R-i) -^ max, (2^ И-^МОИлдка) + A2|M-)||^r(Kd) < АХД2 + А2. (8) Переходя к образам Фурье, а затем расширяя задачу, переходя к мерам, получаем следующую задачу (здесь опять для удобства рассматривается квадрат значения задачи (8)) j 1|2“ фи(т) -д max, КД j d^F\2 I (1 + ||1||2)г^(1) кд кд < АхД2 + А2 Пользуясь теми же соображениями, которые применялись ранее, нетрудно показать, что dp^ = АД- — т) является решением и этой задачи. Таким образом, значение задачи (8) равно тоже VR. Рассмотрим теперь такую задачу: для фиксированной функции у(-) G Г^ЖУ найти величину )™К«) ( (2тг)й ^^ ^'^МВД) + МИ')1|^(ВД) Нетрудно убедиться, что решением этой задачи является функция жу(-) такая, что F^W -— ----- WY Ат + А2 (1 + ||1||2) Введем в линейном пространстве Н = L2(Rd) х ^(R^) полускалярное произведение (zV)H = ^|р У (Ai^(t)^(t) + Аз (1 + \\t\\2Y Fz^Fz2^ dt кд (здесь г1 = (z^ (•), ^(J), z2 = (z2(-), z^-))) и соответствующую полунорму обозначим через || • ||я- Тогда задача Н может быть записана в следующем виде ||(Еж(-),ж(-)) - (у(-),0)||я ^ min, ж(-) е T/afR6'). (10) Поскольку жу(-) — решение задачи (10), то производная минимизируемого функционала в этой точке равна нулю, т. е. для всех ж(-) G T/at^) имеет место равенство ((Яжу(-),жу(-)) - (у(), 0), (Еж(-),ж(-)))н = 0. Отсюда следует, что ||(^ж(.),ж(.)) - (у(-), 0) ||^ = ||(Еж(-),ж(.)) - (Ежу(.),жу(.))||2я + II (^жу ("), жу (")) - (у('),0)11н- (11) Если ж(*) G Я^(Rd) и ЦРж(-) - у^\\ь2 ^^^^ ^ 6. то из (11), полагая А(-) = ж(-) — ^(О? получим II (-^('), ^('))Ия ^ ||(Еж(.),ж(.))-(у(.),0)||2я < А1А2 + А2. Поэтому для всех ж(-) G Я^К^) таких, что ||Рж(-) — у(-)ЦщкД) С 5, имеем \\D“x^-D“xy^\\M с sup{ ||П“ж(-)||22(кй) : ^7||Еж(-)||22(кй) + А2||ж(-)||^(кй) ^ AiA2 + А2 j> = Vk. Тем самым доказано, что метод D“x^ ~ -----тДтУ^ Дт, У А1 + А2(1 + ||т||2)’-^ ' кд является оптимальным. Остается лишь подставить выражения для Ai и А2. > Предположим теперь, что преобразование Фурье функции известно с ошибкой не на всем пространстве Rd, а на некотором измеримом множестве Q С R^. Тогда соответствующую погрешность оптимального восстановления определим равенством E(D“,HU<dV5,^=mi sup ||Р“ж(-) - ^(y)(-)||L2m, V $(..KHU<d'l, yEL.W 1Я^(-)-у(-)||ь2(е)^5 где нижняя грань берется по всем операторам у: L2(Q) —> L2(Rd). Нетрудно убедиться, что при Qi С П2 Е^Па,Н^<У,б,О^ > E^Da,H^ Оказывается, что существует множество По С Rd такое, что для всех измеримых П, для которых Qq С П С Rd, имеет место равенство Е(,Па,Н^Жа),5,0) = E^D^H^VVY Иными словами, для максимально точного восстановления производной порядка а в метрике пространства L2(Rd) достаточно знать преобразование Фурье на множестве Qq,а использование приближенной информации о преобразовании Фурье в более широких областях не приводит к уменьшению погрешности оптимального восстановления. В одномерном случае этот эффект был обнаружен в работе [10]. Точный результат здесь формулируется следующим образом. Теорема 2. В условиях и обозначениях теоремы 1 положим По = е Rd : . > ~fl - А2/ГГ 1 А2^"^) У I (1 + lkll2) г^"1 \ /J Тогда для всех измеримых П таких, что По С П С Rd, имеет место равенство E^^H^V^S,^ = 5(D“,H’'(Rrf),5), а метод D ЗСД) ~ /п ха ----------ГД^ л 1 + ~ТД7---ГДТТ (Х +) г A - А2А является оптимальным. < Схема доказательства этой теоремы та же, что и предыдущей. Остановимся лишь на некоторых отличиях. После перехода к образам Фурье функция Лагранжа расширенной задачи будет иметь вид (считаем сразу, что Aq = — 1) C^dp^Y Ai, А2) — J f—11|2“ + АхуцД) + А2 (1 + ||Д2) ^ dp^tY кд где %q(-) — характеристическая функция множества И. В силу доказанного в теореме 1, определения множества По и того, что По С И, имеем -И2“ + Aixq(£) + А2 (1 + ||t||2) > 0 при всех t t Л. Далее доказательство оценки снизу проводится так же, как и в теореме 1. При оценке сверху надо рассмотреть линейное пространство Н = L2(H) х У/ДК^). Полускалярное произведение в нем следует определить равенством (Л^2)я ^~^А1 у ^(1)^(1)^ +А2 у (l + ||t|| ) Fz^BjFz^Bjdt. Q КД В остальном доказательство то же, что и в теореме 1. > Рассмотрим теперь несколько примеров для случая d = 2. Пусть а = (1,0) и г = 2. Иными словами, рассматривается задача восстановления частной производной ж41 (-, •) на классе К^^2)- Из теорем 1 и 2 получаем, что при 0 < б < я е^°\н2^2^^ = J-V№^7), множество насыщения Qq представляет собой два круга с центрами в точках EaJtv ,б и радиусами у/л/б — 1, а метод ^t^H,^) ~ ^1 Qo гтху(т1, -7-2)е1(т1*1+т2*2) 1 + б2 4тг(тг — 5) dTi dr^ О+т2+т^ является оптимальным. Вид множеств насыщения Qq Для рассматриваемой задачи при ряде значений б представлен на рис. 1. 1+р2 < 1 - -1/4 pV|sin2?|. Эти множества при ряде значений б представлено на рис. 2.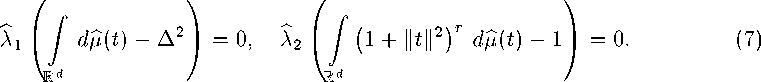
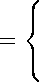
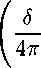
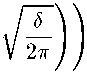
Список литературы Оптимальное восстановление производных на соболевских классах
- Смоляк С. А. Об оптимальном восстановлении функций и функционалов от них: Дис.... канд. физ.-мат. наук.-М.: МГУ, 1965.
- Micchelli C. A., Rivlin T. J. A survey of optimal recovery//In: Optimal Estimation in Approximation Theory/Eds. C. A. Micchelli and T. J. Rivlin.-New York: Plenum Press, 1977.-P. 1-54.
- Traub J. F., Wozniakowski H. A General Theory of Optimal Algorithms.-New York: Academic Press, 1980.-382 с.
- Micchelli C. A., Rivlin T. J. Lectures on Optimal Recovery.-Berlin: Springer-Verlag, 1985.-P. 21-93. (Lecture Notes in Math.; V. 1129.)
- Магарил-Ильяев Г. Г., Осипенко К. Ю. Об оптимальном восстановлении функционалов по неточным данным//Мат. заметки.-1991.-Т. 50, № 6.-С. 85-93.
- Osipenko K. Yu. Optimal Recovery of Analytic Functions.-Huntington-New York: Nova Science Publ., Inc., 2000.-220 с.
- Магарил-Ильяев Г. Г., Тихомиров В. М. О неравенствах для производных колмогоровского типа//Мат. сб.-1997.-Т. 188, № 12.-С. 73-106.
- Магарил-Ильяев Г. Г., Тихомиров В. М. Выпуклый анализ и его приложения.-М.: Эдиториал УРСС, 2000.-176 с.
- Магарил-Ильяев Г. Г., Осипенко К. Ю., Тихомиров В. М. Оптимальное восстановление и теория экстремума//Докл. РАН.-2001.-Т. 379, № 2.-С. 161-164.
- Магарил-Ильяев Г. Г., Осипенко К. Ю. Оптимальное восстановление функций и их производных по приближенной информации о спектре и неравенства для производных//Функц. анализ и его прил.-2003. (в печати).


