Оптимальные алгоритмы выделения контуров изображения в системе технического зрения

Несомненно, в век компьютерных технологий все большее место в современной науке занимает робототехника. Это связанно с внедрением нового оборудования на заводах, автозаправочных станциях, в аэропортах и в других сферах жизнедеятельности человека. Частью этих нововведённых систем является программа с тем или иным алгоритмом распознавания контуров изображений, например, реализация выделения контуров различных деталей или механизмов. От эффективности данного алгоритма зависит и вся последующая работа роботизированной системы в целом.

В настоящее время существует большое количество различных алгоритмов выделения контуров, но лишь некоторые из них получили широкое распространение, а именно за счет своей универсальности. В этой работе будут рассмотрены наиболее популярные алгоритмы: оператор Кирша, оператор Робинсона, детектор границ Канни и метод Marr-Hildreth [1]. Для тестирования этих методов будет использоваться тестовое изображение (рис.1).

Первым из рассматриваемых методов является оператор Кирша. Этот метод был разработан Русселом А. Киршем в 1971 году [2]. Данный алгоритм основывается на использовании обнаруживающей матрицы (маски), которую последовательно вращают по восьми основным сторонам

Рис. 1. Исходное изображение для обнаружения контуров.

света: север, северо-запад, запад, юго-запад, юг, юго-вос-

ток, восток и северо-восток. После исследования Руссел А. Кирш вывел следующие маски для каждой стороны света [3]:

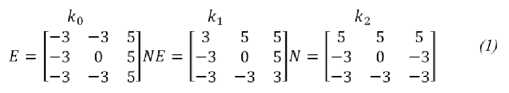
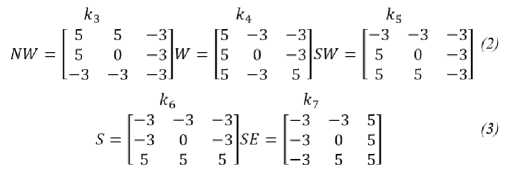
В данном случае величина границы определяется как максимальное значение, которое может быть найдено при помощи маски. Определенная маска помогает направлению выдать максимальную величину. Из этого можно сделать вывод, что маска k0 позволяет выделять вертикальные границы, а маска k5 – диагональные. Из масок так же заметно, что последние похожи на первые четыре, но являются их зеркальным отражением по центральной оси используемой матрицы [4].

В ходе обработки тестового изображения, можно получить следующий результат (рис. 2).

Рис. 2. Идентификация контуров оператором Кирша.

Позднее в 1977 году был разработан оператор Робинсона, который, по сути, являлся аналогом метода Кирша, но благодаря использованию коэффициентов 0, 1 и 2 стал более простым в реализации. Матрицы, которые использует данный оператор, являются симметричными относительно своих центральных осей, каждая из которых заполнена нулями. Благодаря этому можно использовать лишь первые четыре матрицы, а остальные результаты получить, инвертируя первые. Оператор Робинсона будет выглядеть следующим образом[5]:

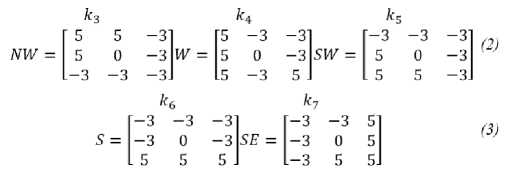
Из матриц следует, что после того, как каждая из них будет последовательно применена к пикселю и его окружению, максимальное значение, которое он получит, будет считаться величиной градиента. Тогда угол градиента можно аппроксимировать как угол линии, заполненной нулями в маске, дающей максимальный отклик.

Как и в предыдущем случае, можно провести обработку исходных изображений (рис. 3).

Рис. 3. Результат работы оператора Робинсона.

Несмотря на простоту предыдущего оператора, наибольшую популярность в итоге получил детектор границ Канни. Метод впервые был описан в 1983 году ученым Джоном Канни в своей магистерской диссертации. Данный метод превосходит по эффективности своей работы многие современные, даже если и был разработан более тридцати лет назад. Его отличительной особенностью является устранение шума на контурах изображения, что, несомненно, оказывает влияние на конечный результат. Данный алгоритм заключается в выполнении следующих шагов:

• •    размытие исходного изображения f(r, c) с помощью метода Гаусса f^(r, c). f^(r, c)=f(r,c)*G(r,c,6);

• •    выполнить поиск градиента. Границы намечаются там, где градиент принимает максимальное значение;

• •    подавление не-максимумов. Только локальные максимумы отмечаются как границы;

• •    итоговые границы определяются путем подавления всех краев, не связанных с определенными границами.

Результатом работы алгоритма являются контуры на изображении. За счет своих особенностей данный метод мало восприимчив к шуму (рис. 4).

Рис. 4. Результат работы метода Канни.

Последний метод обнаружения границ цифровых изображений называется Marr-Hildreth, который был разработан в 1980 году. Он подразумевает под собой обнаружение кривых на всех участках, где наблюдается резкое изменение яркостей групп пикселей. Данный метод является простым и работает при помощи свертки исходного изо- бражения с LoG-функцией или как быстрая аппроксимация с DoG. При работе метода нули в обратном результате обозначают контуры изображения. Для работы метода необходимо придерживаться следующих шагов алгоритма [6]:

• •    размытие изображение методом Гаусса;

• •    применение оператора Лапласа к размытому изображению (часто первые два шага объединены в один);

• •    производится цикл вычислений и в полученном результате смотрят на смену знака. Если знак изменится с отрицательного на положительный и значение изменится более чем на некоторый заданный порог, то необходимо определить эту точку, как границу;

• •    Для получения лучших результатов шаг с использованием оператора Лапласа можно выполнить через гистерезис, то есть так, как это реализовано в алгоритме Канни.

Результат работы данного алгоритма на тестовом изображении будет следующим (рис. 5).

Рис. 5. Результат работы метода Marr-Hildreth.

Исходя из проведенных исследований, можно сделать вывод о том, что для распознавания механизмов и других объектов, состоящих из криволинейных контуров, в робототехнике эффективнее всего может применяться метод Канни, который позволяет добиться наибольшей резкости границ и высокой детализации. Для выделения линейных контуров объектов, например, в тех случаях, если используются системы технического зрения на конвейерных линиях, наилучшим образом подходит метод Marr-Hildreth, который выделяет даже мелкие линейные контуры на изображениях. Таким образом, в робототехнике могут использоваться все описанные алгоритмы выделений, но каждый из них наиболее эффективен на определенном классе задач, а также нацелен на получение результата определенного качества.