Оптимизация частот колебаний упругой пластинки в идеальной жидкости

Данная работа посвящена численному решению экстремальной задачи о поиске минимального собственного числа самосопряженного интегро-дифференциального оператора. Рассмотрим задачу на собственные значения. Необходимо найти нетривиальные решения уравнения d-^ Qh3 (x) ^ ^^’  ^ — A2 Qh (x) U (x, t) + a ^ К (x, t) U (x, t) dt^ = 0

и соответствующие значения A ² , удовлетворяющее граничным условиям:

U | x= - i = U | _{$ =1} = 0,

d2U     = d2U dx2 x=-1 dx2

где x Е [— 1; 1], 0 < t < 1, К(x,t) = — ln выставлено дополнительное ограничение:

j h(x)dx = P,

1 +

/ (i - _a )(i+t)

V (1 - <)(1+ _ж )

/ (i - x)(i+t)

V (i - t)(i+x)

P > 0,

, h(x) Е C ² [ — 1; 1] и на функцию h(x)

^h min

< h(x) <  h _max .

Далее введем функционал:

J (h(x)) = A i ,

где Ai — первое собственное число задачи (1)-(3). В данной работе описывается численный метод, который позволяет определить такую функцию h(x), что J (h(x)) принимает минимальное значение.

Стоит отметить, что уравнение (1) возникает при описании малых колебаний пластинки бесконечной длины и фиксированной ширины в безграничном объеме идеальной несжимаемой жидкости.

Плоскость Оху, в которой происходят колебания пластинки и жидкости, перпендикулярна длинным краям пластинки. Точка А(х = —Цу = 0) и В(х = 1,у = 0) на плоскости Оху соответствуют закрепленным краям. Ширина пластинки равна 2Z (см. рисунок 1). Предполагается, что толщина пластинки является переменной по координате х, то есть h = h(х), и не меняется в направлении оси z (ось параллельная закрепленным краям пластинки). Обозначая через t время, а через и = u(х,t) и Q = Q(х,t) соответственно функцию прогиба пластинки и реакцию жидкости, можно записать уравнение цилиндрических колебаний пластинки:

. 92и , 92 (тл       Eh3                               - p1h9t2 + дх2 vdx2;   Q’    D   12(1 - 12)'                     (5)

Здесь D — жесткость пластинки при изгибе, Е — модуль Юнга, 9 — коэффициент Пуассона, р 1 — удельная плотность материала пластинки. Для определенности примем следующие граничные условия в точках А и В, соответствующие шарнирному закреплению концов пластинки:

I       I              9 2к 9 2U и|л = и|в = 0,    9^ = ЭА =0-                        (6)

^х л ^х в

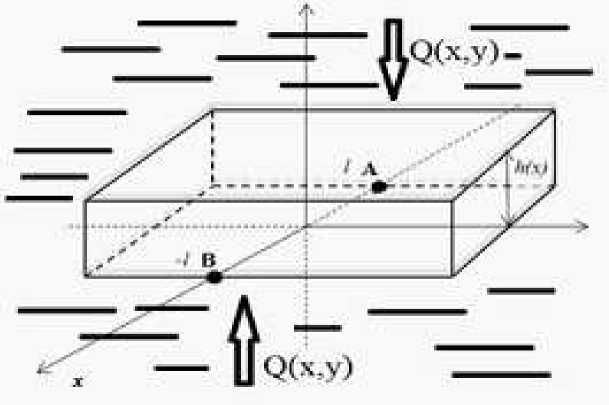
Рис. 1.

Движение жидкости предполагается безвихревым с потенциалом поля скоростей у = ^(х, у, t), удовлетворяющим уравнению Лапласа и линеаризованным граничным условиям

9 2 ^   9 2 ^

9х²   9у 2

9^       ди

⁹у ( х, _е)      ^9t '

9^          ди

⁹у ( х, - _е) ~ ^9t

— I < х <  I, е >  0.

Граничные условия (8) получены путем сноса на ось х условий непротекания жидкости через поверхность пластинки. При этом используются предположения о малости прогиба и, гладкости функции h(х), а также о безотрывности движений жидкости и пластинки.

Распределение давлений р = p(х,у,t) в жидкости вычисляется с помощью интеграла Коши-

Лагранжа

Р = Р ^

^р [#+2 ^{( v}^ ^{) 2}] ^ ^р »

9^

Р2 9Й’

где Р 2 — плотность жидкости, р ^ — давление жидкости на бесконечности. При выводе данного соотношения учтен тот факт, что скорость жидкости мала на бесконечности. Соотношение (9) позволяет определить р, если найден потенциал р. Реакция жидкости Q(х,t), фигурирующая в правой части уравнения колебаний (1), определяется линеаризованной формулой

Q = Р - Р+, где через р+ = (р(х, 0, t))+ и р = (р(х, 0, t)) обозначены распределения давлений соответственно для верхнего и нижнего берегов разреза —l < х < l, у = 0. Определяя Q из соотношений (9), (10) и подставляя найденное выражение в (5), можно преобразовать уравнение колебаний пластинки к виду

+ тп      )= Р2 г■;—^).                 (и)

dt ²    Ух² \ Ух²/      \ dt      ot J

Приходим к замкнутой краевой задаче гидроупругости. Гидродинамическая задача (7), (8) об определении потенциала р и задача (6), (11) о колебаниях пластинки являются связанными, так как в граничные условия (8) входят распределения скоростей колебания пластинки, а в правую часть уравнения (11) — производные потенциала р.

Решение задачи (6)–(8), (11) будем искать в виде к = eMtU (х) ,     р = iweMtФ (х, у) .

Для удобства анализа и решения задачи перейдем к безразмерным переменным и обозначениям х' = х/l, у' = у/l,    U ' = U/l,     Ф' = Ф/12,     h' = lh/S             (13)

A ² = 12p i l ⁶ (1 — У ² ) ш²/S ² Е,     a = p 2 l ² /p i S,                        (14)

где S — площадь поперечного сечения пластинки. Штрихи у безразмерных переменных в дальнейшем опускаются.

Подстановка в (12), (13) в (6)–(8), (11) приводит к следующим соотношениям для определения амплитудных функций U (х) и Ф(х, у).

U |

^h ³ 1^ — A ^{2 (} hU -а ⁽ Ф ⁺ — Ф )) = 0, ах² \ ах²)                      "

х=

i = U |

■=1

= 0,

d2U

ах ²

х=

i

УФ

УФ

д ² Ф

У ² Ф

Эх ²   Уу ²

= 0,

d2U

ах ²

■=i

= 0,

^9у (х, е)

Уу / (■

= U,

1 <

х

< 1,

е> 0.

.х,

е)

Таким образом, путем разделения пространственных и временной переменных исходная задача (6)–(8), (11) сводится к краевой задаче (15), (17) на собственные значения для дифференциального уравнения (15) при граничных условиях (16) и связанной с ней граничной задаче (17), (18) для уравнения Лапласа во внешности разреза — 1 <  х <  1, у = 0.

1. Решение гидродинамической задачи

Определим функцию (потенциал) Ф(х,у), являющуюся решением краевой задачи (17), (18). С этой целью рассмотрим вспомогательную функцию W = Ф + г Ф, аналитическую в плоскости с разрезом — 1 <  х <  1, у = 0. Из условий Коши-Римана и граничных условий (18) будем иметь

УФ/Ух = УФ /ду = U,

откуда

• X

ф =

-

и (€)d— + С (у) = f (ж) + С (у).

Задача определения потенциала Ф сводится к отысканию мнимой части аналитической функции W , действительная часть которой на отрезке [ — 1,1] равна

KeW = Ф = f (ж) + С (у).                               (21)

Решение данной задачи легко выписывается (z = ж + гу):

W =Л ( )² [ ¹ ( ) ² f^ dt, 2ттг \z + 1/ У- \t — 1 У t — z

1 С ¹ f (t) + С _

2^г 7-1 , d0

Соотношение (23) служит для определения постоянной С .

Учитывая, что

1 Г1

7 г J-i Vt2 — 1’ из (23) можно получить

_С = 1 f ¹

⁷¹ У- 1 V— ² — 1.

Используя далее выражение (22) для С и формулу

1 Г ¹ У € + 1 А ² de =1 / z +1 А ² - 1

27 1-1 U — М € — z 2 ^z — 1)    2 ’ выполним следующие преобразования в представлении (22) для W:

• 1    ( z — 1 А ² Г ¹ / € + 1 А ² f(€)d€ С Г _( z — 1 А21 2^ +1J Li V— — 1- € — z ⁺2[ V + 1) ]

• 2    1 f <«

• ^{2 72} \^{z +1}У У- 1      \^{— —} 1У \^{— — z € +1}У ²

• Vz2—I f1    f(€)d_€

27г J-1 (€ — z)V€2-"T2 .

Вычислим величину Ф+, переходя к пределу в (22) при z = ж + гу ^ ж + 20 (0 < у ^ +0) и выделяя в полученном выражении мнимую часть

Ф+ = lim [Im W(ж + 2у)] = — V1  ж2 (у.р. / ----f (€)d€.

^-+0                             27             -1 (€ — .ж    '€

Для разности потенциалов на верхнем (плюс) и нижнем (минус) берегах разреза имеем

Ф+ — Ф- =2Ф+,(29)

Преобразуем интеграл (28), используя определение интеграла в смысле главного значения:

2ф + =i к„. [¹ (е—ж ^{а 2} f(ts^=

7 \ У-1 V ^{1 — t2} ) ^{t —} ж у

Выполняя далее интегрирование по частям, используя выражение (20) для /(t), обозначая через К(t, x) ядро интеграла, получим

2Ф + = lim 6 —^0

[к (x — e, x) j   U (t) dt — К (x + e, x) j U (t) dt — - j    К (t,x)U (t) dt — У     U (t) dt .            (31)

Стоит отметить, что все выражения в правой части (30) (записанные в квадратных скобках) конечны, и, следовательно, применение интегрирования по частям законно. При е ^ 0 сумма первых двух членов в (31) обращается в нуль, а два последних интеграла сходятся. Таким образом, искомая зависимость величины скачка потенциалов Ф+ —Ф-= 2Ф+ от распределения прогибов пластинки имеет вид

2Ф ⁺ =

f.

К(t, x)U(t)dt.

Подставляя найденные величины в (15) и в (16), придём к уравнению (1) с граничными условиями (2).

2. Описание метода решения

Обозначим левую часть уравнения (1) через LU и перепишем его в следующем виде: LU = 0. Тогда из соотношения (LU,U ) = 0 и из уравнения (1) можно выразить собственное число

А ²

________J-^M^S)^________

Jj^ h(x)U ² (x)dx + a J [ _ ₁.₁] _х [ _ ₁.₁] К(x,t)U (x)U (t)dxdt

Получим необходимое условие оптимальности в задаче (1)–(4). Выписывая для этого уравнение Эйлера по h для функционала (33), имеем

^ ^U -    " ² = = 2 ,

^х

где с ² - множитель Лагранжа.

При решении подобных задач с применением известных алгоритмов оптимизации требуется на каждом шаге алгоритма определять величины U (х) и А, удовлетворяющие условиям (2), (3). Для этой цели в данной работе используется метод последовательных приближений.

Для численной реализации этого метода удобнее перейти от уравнения (1) к системе уравнений вида:

(             h^u^ = у

I У тт = А (hu + a J .1 К (t, x)u(t)dt^

Тогда граничные условия (2) могут быть переписаны в следующем виде:

^uL = - 1 = ^и т=1 = ^y| T= - 1 = ^у| т=1 = 0                            ⁽³⁶⁾

Согласно методу Чернусько организуем итерационный процесс

J          h^u^ = y ^{( s +1)}

[ уТТ ') = hu ^s + a J ¹ ₁ К (t, x) u ^{( s )} (t) dt

A ^{( s +1)} =

k"L-.u'"-4

(hu ^{( s +1)} + a J ¹ ₁ К (t, x) u ^{( s +1)} dt, u ^{( s +1)} )

Итак, возникает следующая задача: определить функции и(х) и у(х) и управляющую функцию h(x), удовлетворяющие уравнениям (37), граничным условиям (36) и ограничениям (3) и также, чтобы первое значение А из (1) принимало минимальное значение.

Для решения этой задачи применяется метод проектирования градиента. Для реализации этого метода необходимо выразить вариацию оптимизируемого функционала через вариацию управляющей функции h(x):

s а =

J-^

А u²) Sh dx

Д ^г-и^{2 +} au J k₁ К (t, х) и dt ) dx

.

Для численного решения задачи вводим разностную сетку { x q , х ₁ , ..., х „ } с постоянным шагом Ах = x _i +₁ — x _i , i = 0, . .. , V — 1. Функция h(x) аппроксимируется кусочно-постоянной функцией вида:

h(x) = h _i      при x _{i- 1} <  x <  x _i , i = 1..V,

где h i — некоторые константы. Тогда оптимизируемый функционал А становится функцией V переменных, т.е.

А = F (h 1 , ^ 2 , ..., h _N ).

Для оптимизации этой функции применим метод градиентного спуска. Формула (39) позволяет определить производные SA/Sh i , а именно

5А sh i

34 - ^А -

E N₌₁ h , u ,² + a EN x EN =i К _зк и , - k A x ’

i = 1..V.

Чтобы учесть ограничения (3) применим метод проектирования градиента.

Пусть проекция точки а на гиперплоскость имеет координаты (х ₁ , х ₂ , ..., x n ). Для нахождения этой точки необходимо решить следующую классическую задачу на условный экстремум

Откуда следует, что

X i

Е^1 ^{( x} i ^{— a} i ^{) 2} Ax E _i ^N =₁ X i

^ min, = Р.

V (e ^{a i -} AX)

Пусть решается задача минимизации фундаментальной частоты. Тогда градиентный метод заключается в построении последовательности {h _i } ^N q .

Обозначим

— k+1 h i

, _k дА = ^h i ^{—a k} d>hi ,

тогда

7 ।      ~ k+1

h k⁺¹ = h i

— - fz ^/r i ^{k +1} — .

V y~1       Ax j

Учитывая симметрию задачи относительно точки х = 0, будем искать решение на интервале [0, 1], выставив в точке х = 0 граничные условия иж|ж=о — ^ж|ж=0 — 0.

Как было отмечено выше, задача на собственные значения (в данном случае речь идет о первом собственном значении) решается методом последовательных приближений. Для численного решения используется центральная разностная схема, аппроксимирующая уравнения (35) с последующим применением метода матричной прогонки.

Дискредитированная задача имеет следующий вид:

''.

k :..

— 2r , + f ^+i =

At ²

a2

2ui + гц+1 A at     у '

(N kiui + c У^ К(tj j=0

, X i )u j At

i,j = 1-^.         (47)

Критерием остановки итерационного процесса является выполнение условия

|A ^{( s +1)} — A ^{( s )} | + ||k ^{( s +1)} — k ^{( s )} || ^ <  e, где e — требуемая точность.

• 3.    Результаты

Стоит отметить следующий факт, что форма прогиба U и толщина k(x) выглядят идентично для жестко закрепленных краев и для шарнирно закрепленных, поэтому будут представлены графики соответствующих функций для шарнирно закреплённых краев.

Рассмотрим шарнирный способ закрепления. Зададим c = 0.025, при этом первое собственное число А = 1,1379, получено без управления, а именно, при константной k(x) = 0.9. В случае, использования функции толщины, которая вычислена по алгоритму, который предложен в данной работе значение собственного числа А = 0, 9578, то есть уменьшение произошло чуть более чем на 15%. На рисунке 2 представлена функция прогиба, толщина показана на рисунке 3. Количество итераций, потребовавшееся для e = 0.001 равно 57.

Для жестко закрепленных краев ситуация аналогичная, только число итераций равно 46.

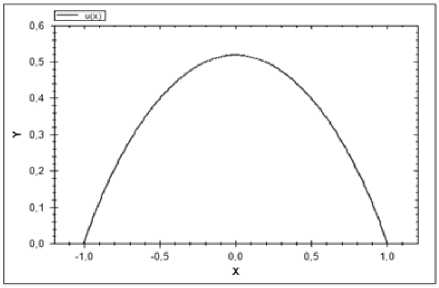
Рис. 2.

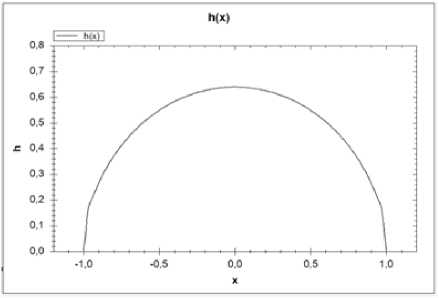
Рис. 3.