Оптимизация ДОЭ, фокусирующего гауссов пучок в прямоугольную фокальную область

В [1] показано, что возможность сведения вычисления двумерного оператора распространения света к вычислению одномерного в радиальносимметричном случае позволяет успешно применять стохастические методы к оптимизации квантованной фазы радиально-симметричных ДОЭ (дифракционных оптических элементов).

Если фазовая функция элемента ф ( u , v ) и амплитуда в сечении освещающего пучка A 0 ( u , v ) = ^I ₀( u , v ) допускают разделение по переменным, т.е.

где

I = ГCx. -a < X < a x 0, иначе

C y -b <  y <  b

0, иначе

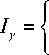
C x , C y – константы, выбираемые из соображений сохранения энергии:

1 ^A

C x = — I" exp ( - 2 и ² / a ² ) du,                 (4)

2a -A     ^{v            7}

ф(и,v) = Ф1 (и) + Ф2 (v) A (u, v ) = A1 (u ) A2 ( v) ,

вычисление двумерного оператора сводится к вычислению двух одномерных и, таким образом, для оптимизации фазовой функции в этом случае также целесообразно использовать стохастические методы. Данная работа посвящена применению такого подхода к расчету квантованного ДОЭ, фокусирующего гауссов пучок в прямоугольную фокальную область. Актуальность такой задачи объясняется широким спектром потенциальных приложений [2], а также тем, что значительное количество технологий изготовления ДОЭ связано с квантованием его фазовой функции [3] и уменьшение числа уровней квантования значительно удешевляет процесс изготовления.

1 ^A

C y =5kI exp ( ^{- 2 v 2/ a} 2 ) ^dv .                   ⁽⁵⁾

^2b -

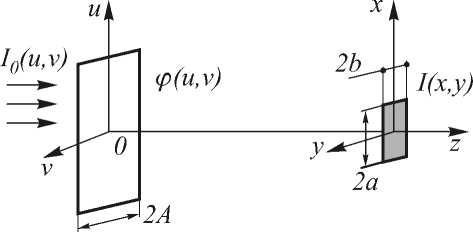
Рис. 1. Постановка задачи фокусировки гауссова пучка в прямоугольную фокальную область

В случае, если ДОЭ с фазовой функцией ф ( и , v ) помещен в заднюю плоскость Фурье-каскада с фокусным расстоянием линзы f , сформированная интенсивность I ( x , y ) в выходной плоскости может быть найдена следующим образом [4]:

Постановка задачи

Рассмотрим задачу фокусировки пучка с распределением интенсивности в сечении

I0 (и, v) = exp (-2 (и2 + v2) Jo2) =

= exp ( - 2 и ²/ a ² ) exp ( - 2 v ²/ a ² )

в прямоугольник с фокальными размерами сторон 2a и 2b с помощью ДОЭ с фазовой функцией Ф ( и , v ) , определенной на апертуре D размером 2A x 2 A (рис. 1).

Определим заданную фокальную интенсивность следующим образом:

^{/( x,y} ) = П? D ^exp и

D

u ²

+ v ² ) / a ² ) exp ( г ф ( и , v ) ) x

x exp (-ik (xu + yv)/f) dudv| .

В случае расчета ДОЭ, включающего в себя линзу:

^/( x’^y ) = "kb Я exp ⁽ " ^{( 21 n} f D

D

и ² + v ² ) / a ² ) exp ( i ф ( и , v ) ) x

xexp ( ik ( и ² + v ² ) /2 f - ik ( xu + yv )/ f ) dudv | . (7)

Учитывая (1), можно переписать формулу (7) в сле-

I = I x ■ l y ,

дующем виде:

I ( x,y ) = I x ( x ) . I ( y ) ,

где

A

I x ( x ) = V ikl^{2 n} f J exp ( - u ²/ ^{CT 2} ) ^X

- A

Cm = J ^ikl2nf exp (-v2/ст2) vp xexp(-ikymv(f + ikv2/2f)dv ,              (16)

x exp ( iф₁ ( u ) ) exp ( iku ²/2 f - ikxu / f ) du | ,

A

I у ( y ) = ^ikl2 n f J exp ( - v ² /ст ² ) x

-A x exp (iф2 (v)) exp (ikv2 /2 f - ikyv / f) dv| .

В этом случае функционал

1 ^a

^Ф ( ф ( ^u , ^v ) ) = 2” J I x ⁽ x ф ^(u) ) ^- C x ^dx + a - a

b

+     J| I y ( У' ^ 2 (v) ) - C y dy

2 b - _b'                           ¹

A = 2 A / N . Отметим, что коэффициенты C n , C m не зависят от выбора фазовых функций ф 1 , ф ₂ и могут быть посчитаны до начала работы оптимизационной процедуры, впрочем, также как и коэффициенты С С x ^, y ^.

Для минимизации функционала (12) в данной работе использовалась модификация известной итерационной генетической процедуры [1, 5].

Перед началом работы итерационной процедуры формировалась начальная популяция, представлявшая собой набор N_gen сгенерированных случайным образом массивов

{ ф ^^¹, Ф j ^е { ( 2 n m / M ) : m ^е [ 1, M ] } •      (17)

характеризует качество формирования заданного распределения интенсивности с помощью ДОЭ с фазовой функцией ф(u,v) = ф1 (u) + ф2(v).

Построение процедуры оптимизации квантованной фазовой функции ДОЭ

Перейдя к дискретной модели с числом элементов дискретизации в плоскости ДОЭ N*N и шагом дискретизации в фокальной плоскости, равным размеру дифракционного пятна A f = Xf Ц 2A ) , можем заменить (11) функционалом

1 N x

^Ф( ф ) = 7T^ I x ⁽ x n ^, Ф 1⁽ u )) - C x ⁺

N x n = 0

1 N y -I

+ _V 2 I y ( y , Ф 2 ( v )) - C y l ,                  (12)

N y m = 0

где N x = 2^ ^A f x n = - a + n A _f , y m = - b + m A _f ,

N y = 2 b / A f .

N - 1

¹x ( x n ) = 2 C P exp ( ⁱ Ф 1 ( u p ) )

p = 0

N - 1

¹y ( y m ) = 2 C m exp ( ⁱ Ф 2 ( ^vq ) ) ,

q = 0

u p = - A + p A , v q = - A + q A,

Cn = J 7ik/2nf exp(-u2/ст2 )x up xexp(-ikxnu/f + iku2/2f)du ,              (15)

Каждый массив содержал последовательно записанные отсчеты функций ф 1 ( u ) и ф ₂ ( v ) :

_ |ф, (-A + jA)      j < N ф = [ф2 (-A + (j - N)A) j > N

Для увеличения скорости сходимости в начальную популяцию вводилось в качестве начального приближения (т.е. одного из «индивидов» нулевой популяции) геометрооптическое решение ф ( u , v ) задачи фокусировки гауссова пучка в прямоугольник, квантованное по M уровням. Такое решение представляет собой суперпозицию двух одномерных фокусаторов в отрезки с длинами 2a и 2b :

ф ( u,v ) = ф 1 ( u ) + ф 2 ( v ) . (19)

Далее, в цикле последовательно выполняются следующие операции:

• -    скрещевание – формирование N_child дополнительных новых индивидов-массивов, значение каждого отсчета которых выбирается как значение соответствующего отсчета случайно выбранного массива-«родителя»;

• -    мутация – стохастическое изменение значений случайно выбранных отсчетов, получившихся новых массивов. Выбор вероятности мутации определяет скорость сходимости алгоритма;

• -    селекция - определение следующей популяции «родителей» путем выбора N_gen лучших (в смысле решаемой задачи) индивидов с помощью вычисления целевых функций для всех индивидов.

Для улучшения сходимости генетическая процедура совмещалась с применением метода вариаций на каждой итерации.

После завершения итерационной процедуры, следующие критерии были выбраны для оценки качества фокусировки: энергетическая эффективность

Nx-1 Ny "*                        Nx-1 Ny - e = 221. (x.) Iy (Ут)/22 CxCy,     (20)

n = 0 — = 0                      / n = 0 — = 0

и среднеквадратичное отклонение сформированной интенсивности от среднего значения I

5 =

N x - 1 ^N , ^- 1

I 22 [ I . ( x . ) I ■ ( у - Н"Т

^ . = 0 — = 0

N . - 1 N y ^-1                        ,

I 2 2 [ I . ■ ( . . ) I, ( y - ) ] ’

I . = 0 — = 0

-

1/2

_   N. - 1 ^N y ^{- 1}                        I

I = 2 2 I . ( x . ) i , ( y — ) KN •

. = 0 — = 0                     /

Результаты вычислительного эксперимента

Для постановки вычислительного эксперимента выбирались следующие параметры: длина волны освещающего пучка Х=10 , 6 мкм, радиус освещающего пучка о =1,85 мм, фокусное расстояние / =100 мм, размер апертуры 2* A =6,4 мм, размер фокальной области 2 a *2 b =1,75*3,5 мм, число отсчетов фазовой функции на апертуре элемента N*N =100*100, число уровней квантования M=8, количество итераций стохастической процедуры N =100, число индивидов исходной популяции N_ge . =20, число индивидов, образованных операцией скрещивания N_chi ld =20.

Уменьшение значения функционала невязки с ходом итераций показано на рис. 2.

б

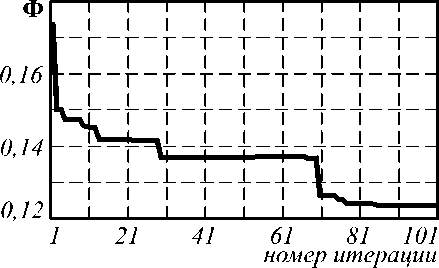
Рис. 2 Зависимость значения невязки от номера итерации

На рис. 3 представлены итерационно рассчитанная фаза ДОЭ ( a ) и интенсивность в фокальной плоскости элемента: ( б) - результат численного моделирования итерационно рассчитанного ДОЭ, (в) -фаза геометрооптического приближения, (г) - результат численного моделирования геометрооптического приближения.

Значения расчетной энергетической эффективности (20) и среднеквадратичного отклонения интенсивности (21), полученные в ходе вычислительного эксперимента для квантованного геометрооптического приближения и итерационно найденного решения, приведены в таб. 1.

Рис. 3. Итерационно рассчитанная фаза ДОЭ (a), (б) - распределение интенсивности, сформированное итерационно рассчитанным ДОЭ в фокальной плоскости (результат численного моделирования), (в) - фаза геометрооптического приближения, (г) - распределение интенсивности, сформированное геометрооптическим приближением

Таблица 1

Метод расчета	e , %	δ ,%
Геометрооптический	87	45
Итерационный	88	13

Таким образом, применение стохастической итерационной процедуры с функционалом (12) позволяет рассчитывать восьмиуровневые ДОЭ, фокусирующие гауссов пучок в прямоугольник с энергетической эффективностью, близкой к эффективности геометрооптического решения, и более чем в 3 раза меньшим значением среднеквадратичного отклонения для выбранного набора физических параметров. Отметим также небольшие вычислительные затраты, требуемые для реализации расчета элемента, что объясняется простотой вычисления функционала (12) после того, как значения коэффициентов (15) предварительно посчитаны.

Заключение

В данной работе рассмотрено применение известной генетической итерационной процедуры нахождения экстремума функции многих переменных к расчету квантованного ДОЭ, предназначенного для фокусировки гауссова пучка в прямоугольник.

Приведенные результаты вычислительных экспериментов подтверждают перспективность рассматриваемого подхода.

Автор выражает благодарность С.Г. Волотов-скому за помощь в постановке вычислительного эксперимента.