Оптимизация двухлистового упругого элемента протеза стопы с использованием линейной и нелинейной теории изгиба

Многие современные конструкции протеза стопы содержат упругий элемент, который представляет собой консольно закрепленную многолистовую рессору с зазорами между листами или без них (см. рис. 1: a – серийный образец, изготовленный на экспериментальном заводе средств протезирования, г. Реутово, Московская область; б – опытный образец упругого элемента, изготовленный в Пермском НИИ композиционных материалов из углепластика КМУ-4Л; в – упругий элемент протеза стопы Carbon Copy , изготовленный фирмой Ohio Willow Wood Company , США [1]; г – упругий элемент протеза стопы Quantum Foot , изготовленный фирмой Hanger Inter Med , Великобритания). Основная проблема, возникающая при конструировании упругого элемента, – обеспечение заданных упругих характеристик и одновременно максимальной прочности.

Упругие элементы указанного вида сейчас активно изучаются, в том числе теоретически, как в России, так и за рубежом [1–9]. Однако полной и адекватной математической модели упругого элемента не имеется и в ближайшее время такая модель, вероятно, не будет создана ввиду значительной сложности конструкции. Разрабатываются упрощенные модели, отражающие поведение упругого элемента в некоторых частных случаях.

В данной работе за основу взята математическая модель, разработанная на кафедре теоретической механики Пермского государственного технического университета [7, 8]. В эту модель внесены новые элементы – учтены зазор между

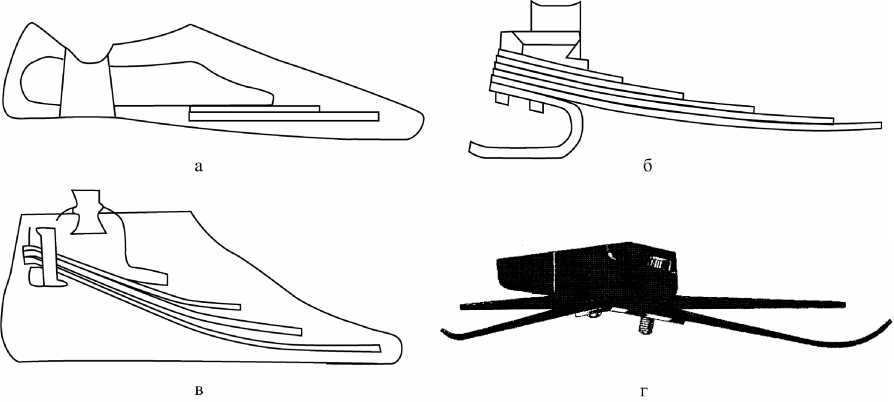
Рис. 1. Разновидности упругого элемента протеза стопы

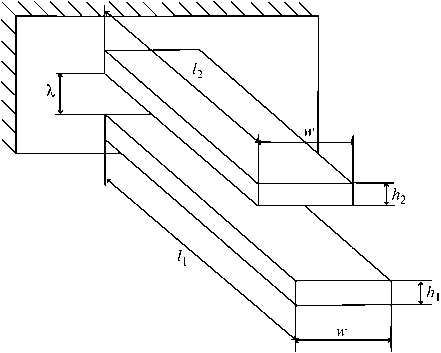
Рис. 2. Модель упругого элемента

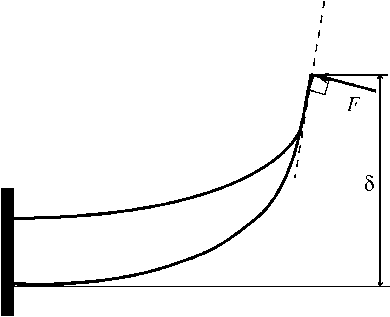
Рис. 3. Схема изгиба упругого элемента

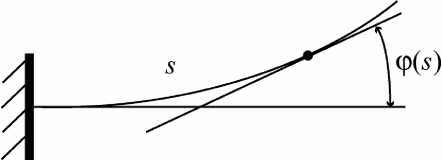
Рис. 4. Функция, описывающая форму изогнутого листа листами и геометрическая нелинейность изгиба листов. В рамках построенной модели решены требуемые задачи математического моделирования двухлистового упругого элемента – расчет изгиба под действием заданной нагрузки и оптимизация конструкции, то есть нахождение параметров элемента, обеспечивающих максимальную прочность при заданных размере и податливости (размер определяется размером обуви пациента; податливость выбирается по желанию пациента или из медицинских соображений). Проведено сравнение полученных результатов с результатами немодифицированной модели (там, где такое сравнение возможно). Показано, что предложенная новая модель дает, вообще говоря, лучшие результаты и, следовательно, может рассматриваться как определенный шаг в направлении построения упомянутой выше полной и адекватной математической модели.

Модель изгиба упругого элемента и постановка задачи оптимизации

Используемая модель упругого элемента показана на рис. 2. В этой модели упругий элемент представляет собой два плоских (в отсутствии нагрузки) листа прямоугольного сечения, отстоящих друг от друга на заданном расстоянии λ ; один край каждого листа защемлен, другой свободен. Листы изготовлены из материала с модулем Юнга E и имеют одинаковые ширины w ; длины l 1 >  l 2 и толщины h 1 , h 2 листов различны (нижний индекс 1 или 2 здесь и далее означает величины, относящиеся, соответственно, к нижнему и верхнему листам). К краю нижнего листа, перпендикулярно ему, приложена заданная следящая сила F , равномерно распределенная по ширине листа (рис. 3). Эта сила моделирует реакцию поверхности при ходьбе на протезе. Под действием силы F листы испытывают совместный изгиб (рис. 3; изгиб не предполагается малым). Геометрически толщины листов считаются равными нулю; реальные толщины входят только в изгибные податливости листов (см. ниже). Изгиб считается цилиндрическим, так что формы листов полностью описываются их профилями. Предполагается, что контакт профилей листов либо происходит только в одной точке (расположенной на краю верхнего листа), либо вообще отсутствует (при достаточно малой величине силы F ). Трением между листами пренебрегаем. Профиль изогнутого листа длины l (не меняющейся при изгибе) описывается функцией ф(s ), где 0 <  s <  l - длина дуги профиля листа от точки защемления до некоторой произвольной точки (криволинейная координата этой точки), ϕ – угол между касательными к профилю в этих точках (рис.4).

Предполагается [10], что в точке с криволинейной координатой s на левую (относительно этой точки) часть листа со стороны правой части действует (сосредоточенный) момент

M = фЧs)/a, (1) где a = 12/Ewh3 - изгибная податливость листа, а “напряжение” (oss на нижней поверхности листа) в этой точке

Eh

^ ( s ) = — ф⁽ s ).

Обозначим через 5 прогиб упругого элемента, то есть расстояние между краем верхнего листа и касательной к профилю этого листа в точке защемления (рис. 3). Введем также обозначение

σ max

= max i max| m ( s )|, max| ^ >( s )| I

V 0 < s <  1 1           0 < s <  1 ₂          J

(максимальное напряжение в упругом элементе). При заданных E , w , l ₁ , F величины δ и σ _max являются функциями l ₂ , h ₁ , h ₂ :

5 = 5( 1 2 , h i , h 2 ),                                            (4)

O max = О max⁽ I 2 , h i , h 2 ).                                    (5)

Как упоминалось во введении, размер l ₁ упругого элемента и его податливость (прогиб δ ₀ при определенной силе F ) заранее заданы; требуется максимизировать прочность (минимизировать σ _max ). Тогда математическая постановка задачи оптимизации принимает следующий вид.

Задача . Для заданных E , w , 1 1 , F , 5 0 , найти 1 2 , h ^ , h 2 , минимизирующие σ _max( l ₂, h ₁, h ₂) при условии

5 ( 1 2 , h i , h 2 ) = 5 o .                                            (6)

Алгоритм численного решения задачи оптимизации

Сформулированная задача оптимизации решалась численно. Вначале был построен алгоритм вычисления функций (4) и (5). Опишем этот алгоритм.

Если контакт между листами отсутствует, то верхний лист остается плоским, а на нижний действует одна сила F (рис. 5). Составляя с помощью (1) уравнение равновесия участка AB нижнего листа (рис. 5), найдем

• - ф " ( 5 )/ a i + FH ( 5 ) = 0,                                (7)

где l1

H ( 5 ) = J cos( ф ₁ ( 1 1 ) - ф 1 ( x )) dx                              (8)

s

– плечо силы F относительно точки A . Подставляя (8) в (7), дифференцируя полученное соотношение по 5 и учитывая, что ф 1 (0) = 0 (условие защемления) и ф " ( 1 1 ) = 0 (следует из (7) и (8)), получим краевую задачу для ф 1 ( 5 ):

ф "' ^{( 5} ) = ^{- a} i ^{F cos(} Ф i^{( 1} 1 ) ^- Ф 1^{( 5} )), ⁰ <  ⁵ <  ¹ 1 ,

< Ф 1 (0) = 0,                                                              (9)

ф " ( 1 1 ) = 0.

Задача (9) неудобна для численного решения, так как является краевой (а не задачей Коши) и, кроме того, содержит неизвестное заранее ϕ ₁ ( l ₁ ) . Поэтому была введена вспомогательная функция

• У 1 ( 5 ) = ф " ( 1 " ) — ф " ( 1 " — 5 )                                    (10)

(геометрический смысл этой функции – отсчитываемый от свободного края листа угол между касательными к профилю листа в точке на этом краю и в точке c криволинейной координатой 1 " - 5 ). Из (9) и (10) получим задачу Коши для ф 1 ( 5 ):

^ 1" ( 5 ) = a 1 F cos ^ " ( 5 ), 0 <  5 <  1 " ,

« ^ 1 (0) = 0,                                                    (11)

у " (0) = 0.

Решив задачу (11), найдем из (10)

ф "⁽ 5 ) = У 1^{( 1} 1 ) ^- У 1^{( 1} 1 ^- 5 ).                                   ⁽¹²⁾

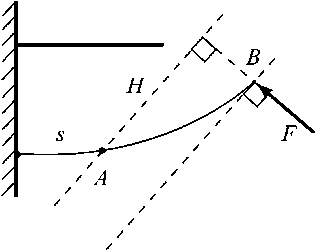
Рис. 5. Схема изгиба листов при отсутствии контакта

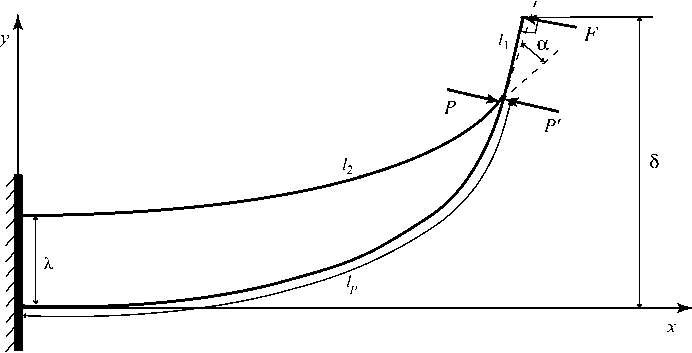
Рис. 6. Схема изгиба листов при наличии контакта

Так как предполагалось, что верхний лист остается плоским, то

ϕ 2 ( s ) ≡ 0.                                       (13)

Это предположение справедливо, если (как следует из простых геометрических соображений)

s

∫ sinϕ1 (x)dx < λ при всех s ≥ 0, таких что s

∫ cos ϕ ₁( x ) dx ≤ l ₂ .                                    (14)

Если условие (14) не выполнено, то между листами происходит контакт. Схема изгиба нижнего и верхнего листов (соответствующая сформулированному во введении предположению о характере контакта) приведена на рис. 6. На нижний лист действуют силы F и P , на верхний лист действует сила P ′ = - P , причем величина силы P , криволинейная координата l_P точки контакта и угол α между силой P ′ и нормалью к профилю верхнего листа в точке контакта (он же угол между профилями листов в точке контакта) заранее неизвестны. Составляя уравнения равновесия участков листов, расположенных между свободным краем и точкой с криволинейной координатой s и вводя вспомогательную функцию

ψ ₂( s ) = ϕ ₂( l ₂) - ϕ ₂( l ₂ - s ),                               (15)

получим, аналогично (11), задачу Коши для ψ ₁ ( s ) , ψ ₂( s ) :

v'1 ^{( s} ) =

<

a ₁ F cos ψ ₁ ( s )

a 1 F cos V | ( s ), 0 <  s <  1 1 - I P , - a i P cos( V 1 ( s ) - V 1 ( 1 1 - 1 p )), 1 1

— 1p < s < 11,

< v 2 ( s ) = a 2 P cos( v ₂( s ) + a ), 0 <  s <  1 ₂

V 1 (0) = V 2 (0) = 0, v' 1 (0) = v 2 (0) = 0.

Функции ϕ1(s) и ϕ2(s) выражаются через решение задачи (16) по формуле (12) и по аналогичной формуле ф2(s) = V 2(12) - V 2( 12 - s).                                (17)

Эти функции зависят от параметров P , 1_P , a : ф ₁ = ф ₁( P , 1_P , a , s ), ф ₂ = ф ₂( P , 1_P , a , s ). Параметры должны быть далее найдены из: а) условия совпадения значений координаты x точки контакта (рис. 6) при их вычислении с использованием сначала ϕ ₁( s ) , а затем ϕ ₂( s ) ; б) аналогичного условия для координаты y ; в) из упоминавшегося выше условия совпадения угла между профилями листов в точке контакта с углом α . Эти условия представляют собой систему трех алгебраических уравнений относительно P , l_P , α :

1P j cosф1(P, 1P,a,s)ds - jcosф2 (P, 1P,a, s)ds = 0, 00

1P

< Jsin ф1( P, 1P, a, s) ds -J sin ф 2( P, 1P, a, s) ds - X = 0,(18)

ф ₁( P , 1_P , a , 1_P ) - ф ₂( P , 1_P , a , 1 ₂) - a = 0.

Окончательно алгоритм вычисления функций (4) и (5) выглядит следующим образом. Сначала численно (методом Рунге – Кутта [11]) решается задача (11). Затем по формуле (12) находится ϕ ₁ ( s ) и проверяется условие (14). Если это условие выполнено, то для ϕ ₂( s ) справедливо (13). После этого находится δ l ₁

5 = J sin ф ₁( s ) ds                                   (19)

и из (12), (13), (2) и (3) находится σ _max . Если условие (14) не выполнено, то численно решается совместно задача (16) (методом Рунге – Кутта) и, с учетом (12) и (17), система (18) (методом Ньютона с численным нахождением производных [11]). После этого из (19) находится δ и из (12), (17), (2) и (3) находится σ _max .

Далее численно находился минимум функции (5) при условии (6). Для этого сначала условие (6) численно разрешалось (методом Ньютона) относительно l ₂ :

1 2 = 1 2 ( h 1 , h 2 ).                                            (20)

Подставляя (20) в (5), получим (вообще говоря, негладкую) функцию двух переменных ( h ₁ , h 2 ), точка безусловного минимума которой ( h ^ , h 2 ) находилась численно (методом Нелдера – Мида [12]). Далее из (20) получаем оптимальное значение 1 2 = 1 ₂ ( h ₁, h ₂)   и из (5) получаем минимальное значение о max :

*                    ,,* ,* ,*.

° max = ° max ^{( 1} 2 , ^h 1 , h 2 ) ^.

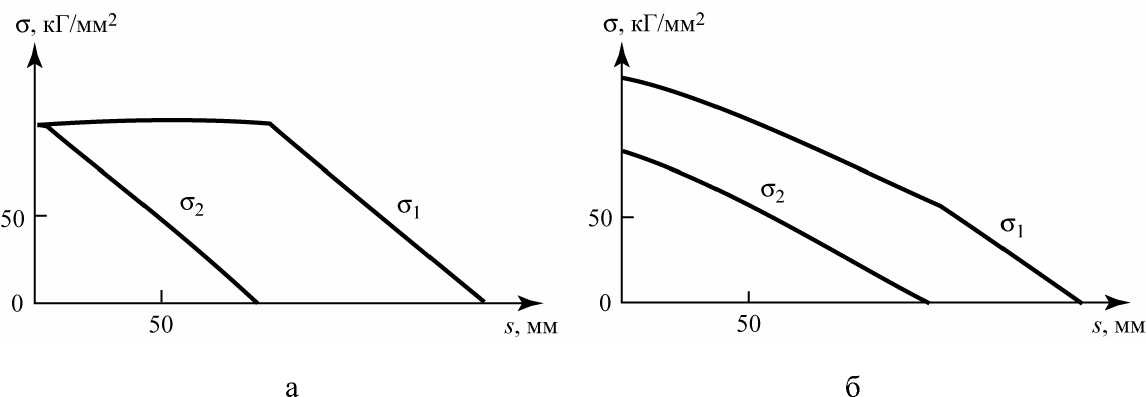
Рис. 7. Напряжения в листах оптимального (a) и неоптимального (б) упругих элементов

Приведем пример результата реализации описанного алгоритма численного решения задачи оптимизации. Все дальнейшие численные результаты соответствуют E = 9533 кГ/мм² (углепластик КМУ-4Л), w = 60 мм , X = 8 мм , 1 1 = 180 мм, F = 1,5 • 80 кГ. При 5 0 = 100 мм описанный алгоритм дает h * = 3,08 мм, h 2 = 2,70 мм, 1 2 = 89,5 мм , a max = 112 кГ/мм². На рис. 7а показаны зависимости с ₁( s ) и ст ₂( s ) для упомянутых оптимальных значений параметров. Для сравнения, на рис. 7б показаны те же зависимости для неоптимальных (но соответствующих 6 = 6 0 ) значений параметров h 1 = 3,25 мм, h ₂ = 2,00 мм , 1 ₂ = 120 мм; для этих значений a max = 145 кГ/мм². Другие примеры приведены ниже (при сравнении результатов, полученных при использовании нелинейной и линейной теорий изгиба).

Аналитическое решение задачи оптимизации с использованием линейной теории изгиба

Проведем линеаризацию соотношений (2), (3), (11), (12), (14), (16)-(19) по параметрам F и λ . Получающиеся приближенные варианты этих соотношений соответствуют линейной теории (слабого) изгиба [10]. Решения (11), (16) и (18) тогда находятся аналитически; после простых преобразований получаем (символом ^~ обозначены величины, найденные в линейном приближении):

(i) если X >  X c , то

£( 1 ₂, h 1 , h ₂) = 4 1 1 FlEwhl, C ( s ) = 6( 1 1 - s ) F / wh 2 , C 2 ( s ) = 0;

где

(ii) если X <  X c , то

δ ( l 2 , h 1 ,

<~ 1⁽ s ) =

h ₂) = 2 ( 2 1 1³ F - 1 22 (3 1 1 -

6 ( ( 1 1 - s ) F - ( 1 ₂

-

1 2 ) P У Ewh l ,

s ) P У wh 2 , 0 <  s <  1 ₂,

6( 1 1 - s ) F/whl, 1 ₂ <  s <  1 1 , ^2 ( s ) = 6( 1 ₂ - s ) P*/wh 2 ,

~

P =

(3 1 1 - 1 ₂) F (к! - XEw) 2 1 2 .

λ c

2 1 2 (V h ³ + v h 3 )

= 2 1 2 (31 1 - 1 ₂) F^wh ^ ;

;

с т_тах ( 1 ₂, h 1 , h ₂) далее вычисляется по формуле (3).

Построение аналитического решения задачи оптимизации, даже для рассматриваемого линейного приближения, сопряжено с весьма громоздкими вычислениями [7]. Поэтому используем здесь предложенный в [7] эвристический метод решения (используемый только в линейном приближении; строгое обоснование метода имеется только для X = 0). Этот метод состоит в том, что условие минимизации

^тах ( 1 ₂, h 1 , h ₂) заменяется на условие

< ( 5 ) = <~₂ (0) для 0 <  s <  1 ₂

(оптимальный упругий элемент должен быть равнонапряженным ). Заметим, что сама возможность выполнения условия (26) существует только в линейном приближении и только в случае (ii). В этом случае условие (26), с учетом (22) и (23), равносильно

~

~

равенствам F = P и < 1 (0) = < 2 (0). Добавляя эти равенства к условию 5 ( 1 ₂, h 1 , h ₂) = 5 ₀

~* ~* ~*

и используя (21)-(24), получим систему алгебраических уравнений для 1 ₂ , h 1 , h ₂ :

' 2 F ( 2 1 1³ - 1 22 (3 1 1 - 1 2 ) )/ Ewh ³ = 5 0 ,

(3 1 1 - 1 2 ) F/h i³ - XEwj21 2

Г = ---------1—,—:----:—гЛ-----

2 1 2 1 h ³ + 1/ h 2 )

. ( 1 1 - 1 2 )/ h i² = 1 2 / h 2 .

<

,

Несложное исследование этой системы приводит к выводу, что при 5 ₀ >  X (это неравенство будем считать выполненным, так как обычно 5 ₀ >>  X ) она имеет единственное (положительное) решение, которое можно представить в виде:

h* = 1 1 (2 F (2 - ц ² (3 - ц ))/( EwS o ) f,

h 2= vhl,(28)

~2* = Mli,(29)

где

M = v 2/(1 + v2),(30)

ν – (положительный) корень уравнения

3(k - 1)v4 + 2v3 + 6kv2 + 2k = 0,(31)

k = ^50 .(32)

Для ν можно найти явное выражение, которое здесь не приводим ввиду его громоздкости. Из (22) и (29) получаем минимальное значение σ ^~ _max :

~ * σ max

l ₁

( ⁵ E²¹ - ^M F J

( 4(2 + 2 m - M ² ) 2 w J

Формулы (27)-(33) дают аналитическое решение задачи оптимизации с использованием линейной теории изгиба. Заметим, что при X = 0 из (28)-(32) получается известный результат [7]: 1 ₂ * Д = 4/13, h ₂* / h f = 2/3 .

Сравнение результатов оптимизации, полученных с помощью нелинейной и линейной теорий изгиба

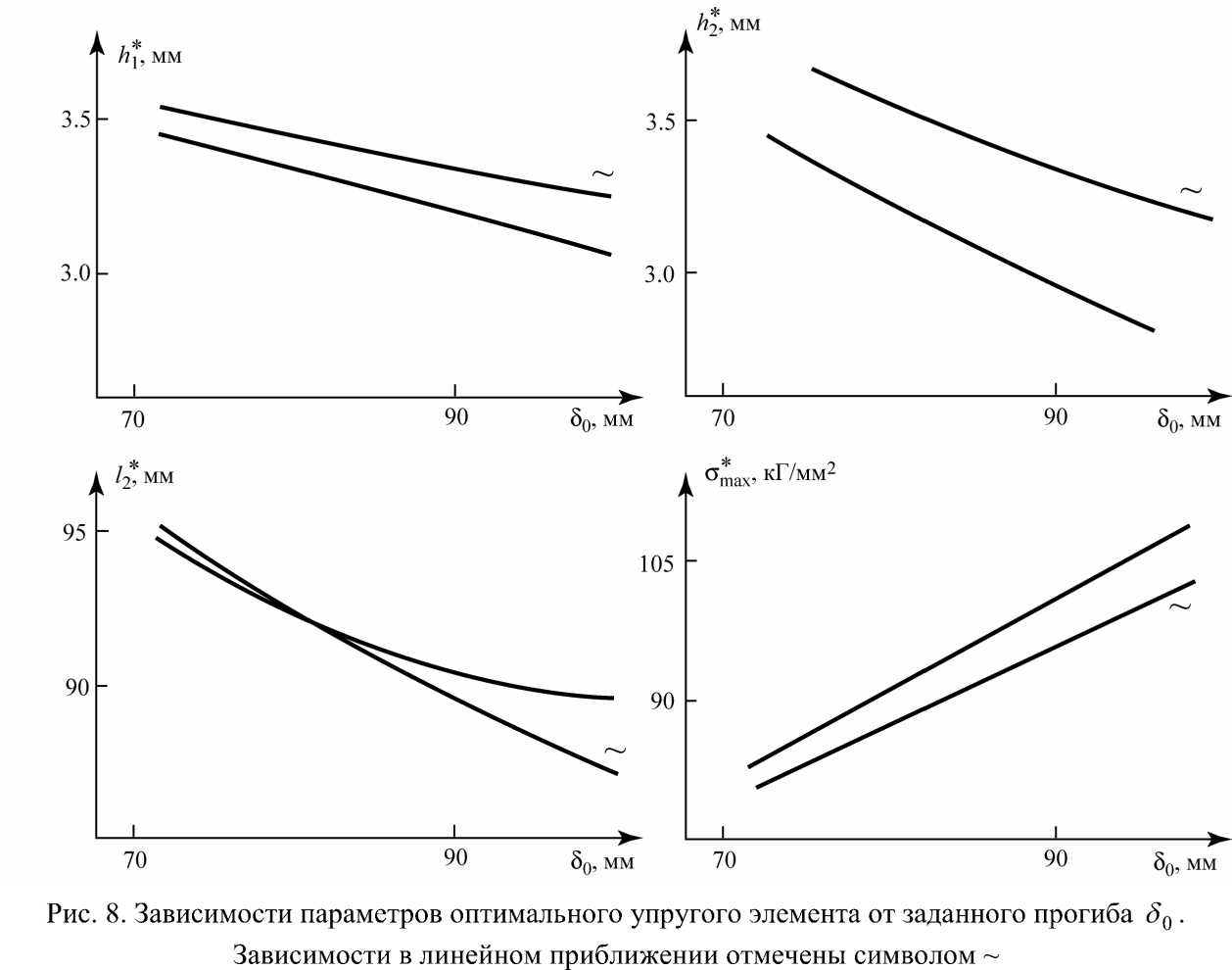
На рис. 8 показаны зависимости оптимальных толщин листов, оптимальной длины верхнего листа и минимизированного максимального напряжения от заданного прогиба δ ₀ . Каждая зависимость приведена для нелинейной теории изгиба и в линейном приближении. При 5 0 = 100 мм погрешности величин h * , h ₂ * , 1 ₂ * , <~ max по отношению к h * , h 2 , 1 2 , о max равны, соответственно, 5,8, 16, 2,7 и 6,3%. Следовательно, линейное приближение дает достаточную точность при вычислении l ₂ , удовлетворительную - при вычислении h / и о max и непригодно при вычислении h 2 . Следует, однако, заметить, что качество линейного приближения определяется не только приведенными погрешностями, но и другими факторами. Во-первых, линейное приближение дает заниженное значение σ _max , что нежелательно вблизи предела прочности материала (94кГ/мм² для углепластика КМУ-4Л). Во-вторых, если с помощью нелинейной теории подсчитать δ для параметров, считающихся оптимальными согласно линейной теории, то эта величина будет заметно отличаться от 5 0 . Например, при 5 0 = 100 мм описанный выше численный алгоритм дает 5 = 86,0 мм

~

~

~

(для h ₁ = h ₁ = 3,26 мм, h ₂ = h ₂ = 3,15 мм, 1 ₂ = 1 ₂ = 87,1 мм).

Выводы

Сравнение результатов оптимизации двухлистового упругого элемента, полученных с помощью нелинейной и линейной теорий изгиба, показывает, что для ряда параметров элемента линейное приближение дает недостаточную точность. Поэтому использование нелинейной теории является необходимым. Вместе с тем, для некоторых параметров линейное приближение приемлемо. Кроме того, линейная теория позволяет проводить качественное исследование задачи. Поэтому в настоящее время обе теории имеют определенные области применения. Вероятно, вопрос об относительной важности этих теорий может быть окончательно разрешен только при исследовании задачи оптимизации многолистового упругого элемента. Переход к многолистовому элементу необходим, так как даже минимизированное максимальное напряжение в двухлистовом элементе при реальном прогибе превышает, как показано выше, предел прочности материала.