Оптимизация низкочастотной балансировки ротора ГД-40

Работа посвящена исследованию возможностей и способов повышения эффективности балансировки ротора ГД-40 на низкочастотном балансировочном станке. Цель работы состоит в том, чтобы численными расчетами с привлечением вероятностно-статистических методов оценить эффективность использования при статической и моментной балансировке не двух, а трёх корректирующих плоскостей.

Исследовательская часть работы содержит три блока:

• 1.    Разработка расчетной модели ротора.

• 2.    Разработка и обоснование вероятностно-статистической модели дисбаланса ротора.

• 3.    Исследование эффективности низкочастотной балансировки гибкого ротора при введении 3-й корректирующей плоскости с использованием предварительных результатов двухплоскостной балансировки на станке «Морион» и ортогонализации трёх корректирующих масс к одной из собственных форм гибкого ротора.

Построение расчетной модели ротора ГД-40

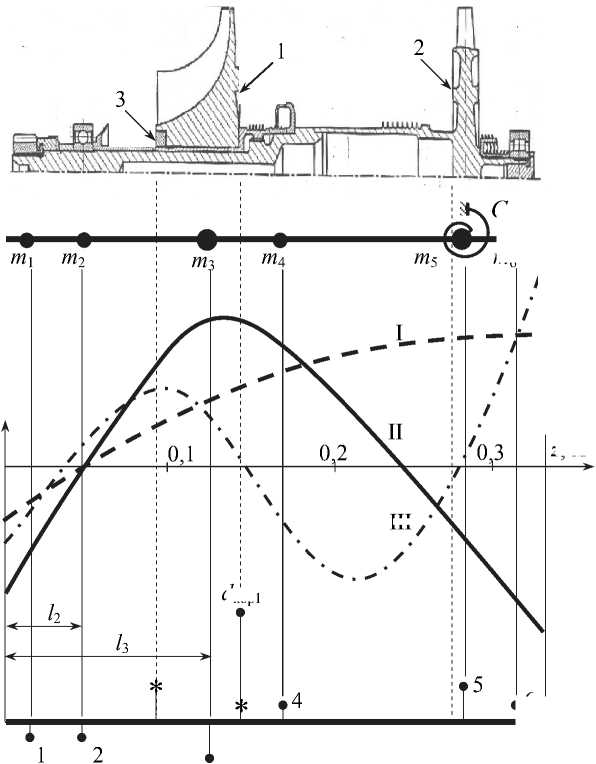
На рис. 1 представлен чертёж исследуемого ротора (a) и его плоская расчётная модель (б), представляющая собой тонкий стержень с шестью сосредоточенными массами в сечениях расположения наиболее крупных насадных деталей. Эти массы учитывают и распределённую массу ротора [1-4]. Спиральная пружина C _ф , моделирует гироскопический момент диска турбины.

Разработана программа, которая определяет критические частоты и собственные формы вращающегося ротора (рис. 1, в), задаёт случайную систему дисбалансов в плоскости xz , вычисляет обобщенные вынуждающие силы на собственных формах и методом главных координат рассчитывает амплитуды колебаний опорных сечений ротора на любых частотах вращения.

Так как рабочая частота ω 0 составляет 60 000 об/мин, то наибольший интерес представляют первые три формы, поскольку ротор при разгоне проходит через первую и вторую критические частоты и работает на частоте, близкой к третьей критической. Расчётные f р и экспериментальные f э значения критических частот ротора приведены в табл. 1. Их сопоставление показывает адекватность используемой модели.

y

II z, м

III dкор1

C ϕ

a)

б)

в)

г)

x

∗ кор2

m 6

Рис. 1. Расчетная схема ротора: a – чертёж ротора; б – расчётная схема ротора; в –

первые три собственные формы ротора ГД-40 на податливых опорах; г – один из неблагоприятных вариантов случайного распределения дисбалансов в осевой плоскости xz и соответствующих корректирующих масс при двух и трёх ( ∗ ) плоскостях коррекции

Таблица 1

Критические частоты ротора

Форма	f р , об/мин (Гц)	f э , об/мин (Гц)
I	14 800 (297)	15 100 (302)
II	28 800 (576)	31 200 (624)
III	94 195 (1884)	95 300 (1906)

Моделирование случайной функции дисбаланса

Известно, что амплитуды вынужденных колебаний системы по k- й форме зависит как от вида и величины случайной функции дисбалансов D ( z ) [5–12], так и от формы колебаний u ( z ), то есть от обобщённых вынуждающих сил Q k :

Qk (to) = to2 J D (z )• uk (z) dz (1) L на тех собственных формах uk (z) системы, частоты которых близки к рабочей частоте или лежат ниже неё, поскольку через эти частоты система проходит при разгоне. Естественно, что при моделировании случайной функции D(z) для ротора ГД-40, работающего на частоте ωкр2 < ω < ωкр3, должны быть вычислены и учтены величины обобщенных сил Q1, Q2, Q3. Что же касается более высоких частот и форм, то здесь отсутствует единое мнение у различных авторов. Большинство считает необходимым учитывать при балансировке гибких роторов до 6–8 собственных форм. Сторонники этой позиции ссылаются на известный факт о низкой скорости сходимости разложения изгибающих моментов в ряд по собственным формам и о столь же низкой скорости сходимости опорных реакций. Заметим, однако, что это справедливо для абсолютно жёстких опор. Реакции же податливых опор пропорциональны амплитудам колебаний, которые сходятся как 1 k4 . Эти соображения говорят о том, что роль высших форм, частоты которых не очень близки к рабочей частоте ротора, менее существенна, чем в случае жёстких опор. Практика низкочастотной балансировки подтверждает этот факт, что позволяет при моделировании случайной функции дисбаланса D(z) потребовать сохранения величины обобщенных вынуждающих сил только низших порядков. При исследовании ротора ГД-40 – это Q1, Q2 и, возможно, Q3.

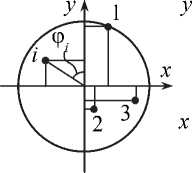
Распределение дисбалансов D ( z , ф) по длине ротора z и по углу ф в плоскости, перпендикулярной его оси, можно представить двумя дискретными функциями D x ( z i ) и D y ( z i ) в плоскостях xz и yz (рис. 2).

i

z

z

i

Рис. 2. Распределение случайных дисбалансов по длине ротора

Далее в работе будем рассматривать колебания в одной из плоскостей, представив дисбаланс ротора D ( z i ) в виде произведения известной сосредоточенной массы модели ротора m i на проекцию e xi или e yi её случайного эксцентриситета e i , предполагая [13-16], что функция ф i является случайной величиной с равномерным распределением. Тогда

D xi = m_te x _t в .                                                                                              (2)

Константу β возьмём для определённости такой, чтобы соответствующая проекция суммарной силы инерции дисбалансов на рабочей частоте равнялась, например, весу ротора P = 3 кГс.

Расчет вынужденных колебаний ротора при различных видах балансировки

Рассматриваются колебания ротора в одной осевой плоскости. Вычисляются виброскорость стационарных колебаний опорных сечений ротора во всем диапазоне частот вращения и амплитуды опорных реакций на рабочем режиме [17–19]. Коэффициент динамичности на всех формах колебаний вала принят равным μ = 10.

Расчеты выполнены при четырех вариантах нагружения:

Вариант 1. Ротор нагружен исходным случайным дисбалансом, который представлен шестью составляющими в точках расположения сосредоточенных масс ротора (рис. 1, б).

Вариант 2. Ротор подвергается стандартной НЧБ в двух плоскостях коррекции. Корректирующие дисбалансы d k = m k · e k определяются системой уравнений:

i m kj - e kj =- z m - e i ;

jz mkj • ekj • lkj =-z mi • ei • 4.

В качестве корректирующих плоскостей используются внутренние поверхности крыльчатки и диска турбины. Они указаны на рис. 1 ( d кор1 и d кор2 ).

Вариант 3. Статическая и моментная балансировка ротора на низкой частоте выполнена в трех плоскостях коррекции. Третьей плоскостью коррекции является левая сторона крыльчатки. В качестве системы дисбалансов используются найденные расчётом в варианте 2 корректирующие дисбалансы d кор1 и d кор2 , являющиеся эквивалентом исходной системы дисбалансов. Вектор корректирующих дисбалансов D 1 , D 2 , D 3 определяется из условия устранения статического и моментных дисбалансов от этих двух корректирующих масс, найденных из системы уравнений (3), (либо определяемых прибором «Морион» экспериментально), а также ортогональности системы трёх искомых корректирующих дисбалансов к вектору второй собственной формы вращающегося ротора на податливых опорах:

z m kj • e kj =- ( m i • e i + m 2 • e 2 ) ;

j = 1

з ,

Z m kj • e kj • lkj =- ( m i • e i • l i + m 2 • e 2 • l 2 ) ^;

Z mkj • ekj • uи (zj ) = 0.

. j=i

Вариант 4. Статическая и моментная балансировка ротора на низкой частоте выполнена в тех же трёх плоскостях коррекции, но вектор корректирующих дисбалансов D 1 , D 2 , D 3 определяется из условия устранения статического и моментных дисбалансов исходных случайных дисбалансов, а также, как и в варианте (3), ортогональности системы корректирующих дисбалансов к вектору второй собственной формы ротора на податливых опорах, то есть:

Z mj • ej =-zmi • ei;

j = ⁱ                 i = ⁱ

3                    6

“ z mj ■ ej ■ lj=-z mi ■ ei ■ lj;

z mj • ej • u II (zj) = 0. I j=i

Результаты расчетов в виде зависимости математического ожидания амплитуды виброскорости левой опоры ротора ГД-40 от частоты вращения приведены на рис. 3. При расчётах использовано 50 вариантов случайного распределения дисбалансов.

В табл. 2 даны численные значения соотношения амплитуд колебаний левой и правой опор ротора при двухплоскостной ( А 2 ) и трёхплоскостной ( А 3 ) балансировке на рабочих оборотах (60 000 об/мин). А 0 – амплитуда колебаний до балансировки.

Таблица 2

Соотношения амплитуд колебаний левой и правой опор ротора на рабочей частоте

Соотношение амплитуд	Левая опора	Правая опора
А 2/ А 0	0,76	0,71
А 3 / А 0	0,55	0,54

Приведенные на рис. 3 и в табл. 2 результаты показывают, что трёхплоскостная балансировка, не требующая практически никаких дополнительных материальных затрат, намного эффективнее двухплоскостной. Более того, практика на предприятии СКБ «Турбина» показала, что двухплоскостная балансировка, дающая очень большой разброс результатов, в 15–20 % случаев приводит к увеличению вибрации ротора. Такой результат, полученный расчётным путём, представлен на рис. 4 (кривая 2), где после двухплоскостной НЧБ вибрации ротора значительно возросли во всём частотном диапазоне. Этот случай соответствует варианту случайного распределения дисбалансов, приведенному на рис. 1, г. Причина повышенной вибронагруженности в данном случае обусловлена неблагоприятным расположением исходных дисбалансов, создающих значительный моментный дисбаланс. Соответственно, корректирующие массы, имеющие малое плечо, оказываются достаточно большими. Расположены же они крайне неблагоприятно по отношению ко II форме колебаний – dкор1 – прямо в пучности, а dкор2 – также в сечении с большой амплитудой, совпадающей по знаку со знаком силы корректирующего дисбаланса. Введение третьей корректирующей плоскости кардинально меняет ситуацию. Появляется возможность выполнить условия ортогональности системы трёх дисбалансов к форме II (система уравнений (4)). Расположение и величина трёх корректирующих дисбалансов показаны на рис. 1, г (∗), а на рис. 4 кривые 2 и 3 наглядно демонстрируют роль условия ортогональности корректирующих балансов ко II форме колебаний.

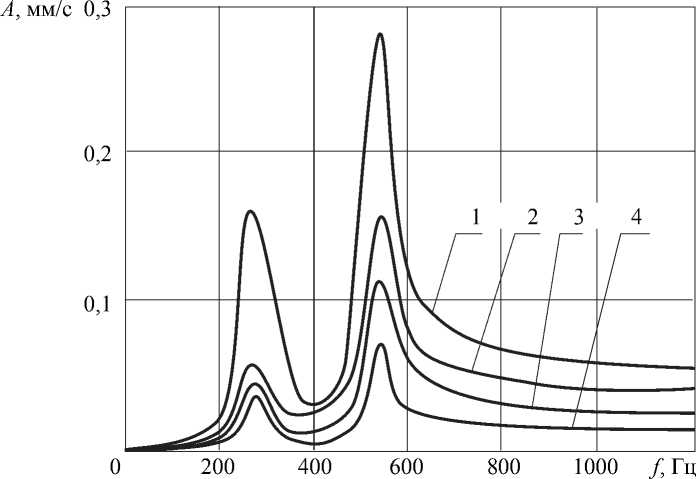
Рис. 3. Математическое ожидание виброскорости на правой опоре ротора ГД-40: 1 – амплитуда виброскорости до балансировки; 2 – амплитуда виброскорости после двухплоскостной балансировки; 3 – амплитуда виброскорости после трёхплоскостной балансировки при моделировании дисбаланса двумя массами; 4 – амплитуда виброскорости после трёхплоскостной балансировки исходных случайных дисбалансов

Применение трёхплоскостной балансировки полностью исключает вероятность повышения виброактивности.

Применение трёхплоскостной балансировки на практике

Для трёхплоскостной балансировки рассматриваемого ротора следует воспользоваться результатом его НЧБ на станке «Морион», после которой в двух плоскостях коррекции (рис. 5) имеются величины ( m 1 e 1 и m 2 e 2 ). Каждую из них следует заменить двумя составляющими: m 1 e 1 x и m 1 e 1 y – в одной корректирующей плоскости и m 2 e 2 x , m 2 e 2 y – в другой. Далее задача сводится к замене двух корректирующих дисбалансов m 1 e 1 x и m 2 e 2 x , лежащих в одной осевой плоскости xz ротора, тремя корректирующими дисбалансами, лежащими в той же плоскости. Эта процедура выполняется с помощью системы уравнений (4). Аналогично заменяем два корректирующих дисбаланса тремя в осевой плоскости yz, после чего две корректирующие массы в каждой из трёх корректирующих плоскостей заменяются их геометрической суммой.

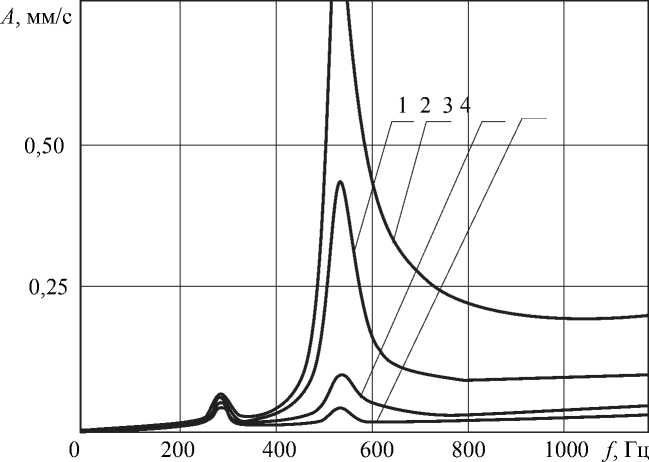
Рис. 4. Амплитудно-частотная характеристика при неблагоприятном распределении дисбалансов: 1 – амплитуда виброскорости до балансировки; 2 – амплитуда виброскорости после двухплоскостной балансировки; 3 – амплитуда виброскорости после трёхплоскостной балансировки при моделировании дисбаланса двумя массами; 4 – амплитуда виброскорости после трёхплоскостной балансировки исходных случайных дисбалансов

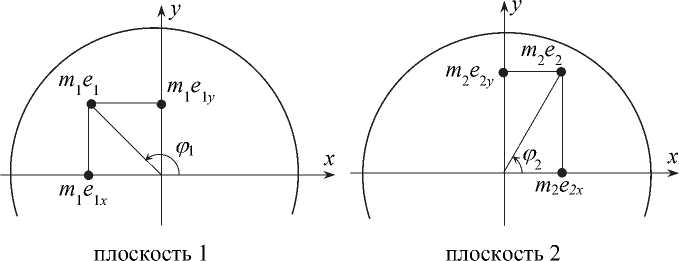
Рис. 5. Корректирующие массы в 2 плоскостях коррекции

Выводы

• 1.    С использованием вероятностно-статистической модели случайного дисбаланса ротора расчётным путем получен результат, часто наблюдаемый на предприятии, – повышение уровня вибраций ротора на номинальных оборотах после низкочастотной балансировки. Показано, что причиной этого является близость одной из плоскостей коррекции к пучности второй собственной формы вращающегося ротора.

• 2.    Трёхплоскостная балансировка с использованием даже не лучшей, но доступной плоскости коррекции, позволяет значительно снизить амплитуды виброскорости на рабочем режиме, одновременно уменьшив разброс результатов и полностью исключив случаи повышения уровня вибраций.

• 3.    Предложена методика практической реализации трёхплоскостной балансировки с использованием станка «Морион», осуществляющего низкочастотную двухплоскостную балансировку ротора.