Оптимизация ортодонтического перемещения зубов

При планировании процесса исправления зубочелюстной аномалии врачу-ортодонту необходимо понять, куда и каким образом необходимо переместить зуб. Изменение его положения происходит посредством действия на зуб определенной © Дубинин А.Л., Няшин Ю.И., Осипенко М.А., Еловикова А.Н., Няшин М.Ю., 2016 Дубинин Алексей Лаврентьевич, ассистент кафедры теоретической механики и биомеханики, Пермь Няшин Юрий Иванович, д.т.н., профессор кафедры теоретической механики и биомеханики, Пермь Осипенко Михаил Анатольевич, к.ф.-м.н., доцент кафедры теоретической механики и биомеханики, Пермь

Няшин Михаил Юрьевич, к.ф.-м.н., Пермь системы сил, приложенной в определенном месте, которую развивает корректирующая конструкция (брекет-система, эластопозиционер, аппараты внеротовой тяги). В случае чрезмерной силы высока вероятность повреждения тканей пародонта и, как результат, осложнение процесса лечения. В случае же недогрузки лечение может затянуться. Выбор неправильного места приложения ортодонтической нагрузки (т.е. места крепления или действия аппарата) может привести к результатам, отличающимся от запланированных, например совершение зубом сложного движения (в медицинской литературе распространен термин «наклонно-вращательное движение») вместо ожидаемого поступательного, движение не в желаемом направлении, недостаточный поворот зуба и прочее.

Исследования по влиянию величины силы на процесс ортодонтического перемещения зубов в альвеолярном отростке начались еще в середине XXI в. При обобщении результатов многочисленных натурных экспериментов на обезьянах и собаках было предложено несколько теорий, объясняющих данный процесс (Томс (1859), Кингслей (1880), Валькгофф (1890), Сандстедт (1907), Оппенгейм (1910)) [2].

Калвелис пишет [5]: «Установленные Оппенгеймом тканевые изменения при ортодонтическом перемещении зубов в своей основе соответствуют современному представлению по этому вопросу». Оппенгейм утверждал, что под действием нагрузки зуб давит на окружающие ткани. В зонах сжатия преобладает процесс рассасывания костной ткани, а в зонах растяжения поисходит преимущественно образование новой кости (рис. 1). Здесь важно использование слов «преобладает» и «преимущественно», так как другие теории подразумевали лишь односторонний процесс. Любая перестройка кости обеспечивается наличием соответствующих клеток остеобластов и остеокластов, и наличие их в молодой растущей кости свидетельствует о происходящей постоянной перестройке её в период роста и развития. Также заслугой Оппенгейма является выдвинутое им положение о нецелесообразности применения в ортодонтии больших сил, так как это может вызвать повреждение периодонта [5, 12].

Первую количественную оценку величины применяемых сил в ортодонтии дал Шварц (1932) [15], определив четыре степени реакции периодонта в зависимости от величины давления, определяющего характер тканевой перестройки пародонта. Шварц провел эксперименты на собаках, применяя аппараты с пружинами, создающими силу

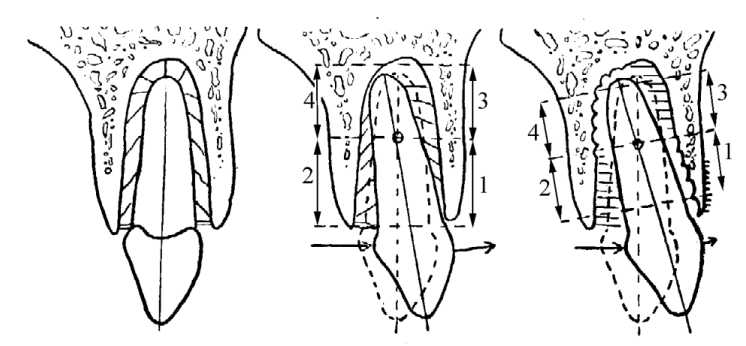
а б в

Рис. 1. Схема ортодонтического перемещения зуба в продольном срезе: а – нормальное положение зуба в альвеоле; б – наклонное положение зуба после воздействия силы; 1, 4 зоны сжатия; 2, 3 зоны растяжения; в – схематическое изображение рассасывания (зоны 1, 4) и новообразования (зоны 2, 3) кости альвеолы определенной величины. Он установил, что величина давления от 3,5 до 26 гс/см2 создает биологически оптимальные условия для ортодонтического перемещения зубов, в то время как при давлении в 67 г/см2 обнаруживается травматическое ущемление периодонта в зоне сжатия. На практике, в целях избежания анемизации и некроза периодонта, давление в периодонте в результате действия внешних сил не должно превышать кровеносного давления в капиллярях.

Советские и российские ученые также внесли большой вклад в изучение данного вопроса. Катц (1930) занимался изучением внутренней структуры челюстей, способствуя более детальному пониманию тканевых преобразований при ортодонтическом лечении [1]. Калвелис (1961) наиболее полно описал сущность основных преобразовательных процессов в опорных тканях при ортодонтическом вмешательстве [5]. Он замечает, что подсчеты Шварца не могут быть определяющими для всех случаев, а решающую роль играет индивидуальная реактивность организма.

Естественной целью исследователей стало оптимизировать процесс перемещения зуба. Обзор источников [1, 2, 5, 8, 9, 12, 15] показал, что факторов, влияющих на выбор величины силы, достаточно много. Необходимо учитывать возраст пациента, пол, состояние соматического и психического здоровья, тип перемещения зубов, место зуба в зубном ряду, геометрические параметры корня зуба (длина, площадь), окклюзионные соотношения, сроки перемещения, особенности пародонта и строения компактного и губчатого вещества челюстных костей, место приложения нагрузки. Еще 50 лет назад трудность определения всех этих индивидуальных характеристик организма человека, учета механических факторов заставляла осторожных ортодонтов применять одинаково малые силы для всех пациентов и во всех случаях.

С течением времени стали появляться некоторые количественные рекомендации по дозированию сил с учетом градации по каким-либо факторам (табл.) [3, 7, 8, 10]. Данные значения, вероятно, получены экспериментальным путем и являются весьма редкой информацией.

Таблица

Варианты дозирования сил

Источник	Величины сил с учетом градации по разным факторам, гс
Райтен (1968) [7]	Наклон: 50–75	Поступательное движение: 70–90
	Экструзия: 25	Интрузия: 50
Губская (1982) [3]	Градация по топографии зуба, возрасту пациента, типу движения
	Наклон: 50–320	Поступательное движение: в 4 раза больше, чем для наклона
Проффит (2008) [8]	Наклон: 50–75	Поступательное движение: 100–150
	Экструзия: 50–75	Интрузия: 15–25
Буклет Bioforce (2010) [10]	Градация по топографии зуба и длине корня 50–320

Биомеханика в ортодонтии.

Понятия центра и области сопротивления зуба

Для исследования начального перемещения зуба под действием приложенной системы сил Фишем в 1917 г. было предложено понятие «центр сопротивления зуба» [11]. Корректное математическое определение, условия существования и описание свойств данной точки было дано в 1999 г. группой ученых М. Осипенко, Ю. Няшиным, М. Няшиным [14].

В данной работе использована следующая модель: зуб представляет собой абсолютно твердое тело, частично погруженное в линейно-упругую среду (периодонт). В отсутствие нагрузки положение зуба считается устойчивым равновесием. При приложении нагрузки зуб совершает малое перемещение. Вследствие линейной упругости среды связь действующей системы сил и получаемых перемещений описывается следующей зависимостью:

ˆˆ _F

_ˆ T ˆ _M

где р - перемещение полюса, ф - вектор малого поворота зуба, матрицы ос, ^у , у характеризуют податливость среды, F – главный вектор системы сил, M – главный момент системы сил относительно полюса.

В работе [14] утверждается, что центр сопротивления зуба и его окружения определяется как точка, удовлетворяющая двум требованиям:

• 1)    если F = 0, то u ( r_CT ,) = 0 для любого M (если нагрузка приводится к паре сил, то зуб поворачивается вокруг центра сопротивления),

• 2)    если M= r^xF , то ф = 0 для любого F (если нагрузка приводится к равнодействующей, линия действия которой проходит через центр сопротивления, то зуб перемещается поступательно).

Здесь u является вектором перемещения.

Также показано, что центр сопротивления зуба существует при выполнении условия антисимметричности матрицы у ^у”* . У осесимметричной системы «зуб-периодонт» такое условие выполняется. В случае моделирования данной системы формой, близкой к реальной форме зуба (не имеющей оси симметрии), данное условие нарушается и центра сопротивления быть не может.

Для случаев, когда центр сопротивления не существует, в работах [4, 6]

предложено и исследовано новое понятие «область сопротивления зуба». Оно является естественным обобщением понятия «центр сопротивления» и сохраняет ряд его свойств.

Прямая поступательного воздействия – линия действия силы, заставляющей тело двигаться поступательно. Ось поворота парой сил – линия, вокруг которой поворачивается тело при нагружении парой сил [6].

Тогда областью сопротивления называется минимальная область (множество точек), которая удовлетворяет двум требованиям:

• 1)    всякая прямая поступательного воздействия проходит через эту область, и через всякую точку этой области проходит прямая поступательного воздействия;

• 2)    всякая ось поворота парой сил проходит через эту область, и через всякую точку этой области проходит ось поворота парой сил.

Также показано, что в зависимости от геометрической формы и механических свойств системы «зуб–периодонт» область сопротивления может быть представлена одной, двумя точками или набором точек в виде эллипса.

Постановка задачи оптимизации начального ортодонтического ПЕРЕМЕЩЕНИЯ ЗУБА

Рассматривается ситуация, когда пациент с зубочелюстной аномалией обращается к врачу для ее исправления. На начальном этапе планирования лечения задачами ортодонта являются определить вид зубочелюстной аномалии, механизм ее формирования, возможности организма к росту, и в итоге он должен решить, как ориентировать и куда переместить каждый из неправильно стоящих зубов. Далее встает вопрос о том, как данные зубы переместить в новое положение с минимальным отклонением от запланированного. Крайне важно уметь спрогнозировать процесс лечения еще до его практической реализации и избежать нежелательных эффектов. При этом необходимо помнить, что, имея дело с живыми изменяющимися системами, характеристики и свойства которых зависят от множества факторов (возраст, пол, наличие болезней, травм и т.д.), ортодонт не может постоянно применять одно и то же решение в разных случаях.

В рамках современной концепции «Медицина XXI века» лечение проходит под девизом «четырех П»: прогнозирование, профилактика, персонализация, партнерство врача и пациента (пациент – участник лечебного процесса). Уместно также вспомнить высказывание выдающегося ортодонта Чарльза Бурстоуна: «Биомеханика – это ядро ортодонтической практики». Другими словами, успех лечения не должен зависеть лишь от профессионального опыта и интуиции врача. Поэтому поисками ответов на главные вопросы ортодонтии специалисты из области медицины должны заниматься совместно с биомеханиками. В данной работе описывается некоторое продвижение в области персонализированной медицины.

Таким образом, задача ортодонтии может быть сформулирована как задача теории оптимизации. Для исследования начального перемещения зуба (в рамках периодонтальной связки, до начала перестройки костной ткани) используется разработанная теория центра/области сопротивления зуба. Модель системы «зуб– периодонт» принимается та же, что и в работах [13, 14]. Значение толщины периодонта (вдоль нормали к поверхности корня) выбрано одинаковым по всей длине h = 0,2 мм. Допустимый малый угол поворота зуба в рамках костной лунки ц = 2°. Данная теория позволяет ответить на вопросы о месте приложения, направлении и величине нагрузки, необходимой для конкретного типа движения и величины перемещения.

Критерием оптимизации является минимизация разницы между запланированным начальным перемещением зуба u * ( r ) и тем, которое можно обеспечить в конкретной ситуации u ( r ):

( u *( r ) -u ( r ))² —>min, r eV , u *( r )=р*+ф* rr, r eV ,

где V - область, занимаемая корнем зуба; р * - запланированное перемещение полюса, р*_{ x*,y *, z*} T . ф* — вектор запланированного малого угла поворота зуба вокруг полюса, ф* = {(р x * , ф* , ф*) ^т .

Соотношение (1) может быть также записано в виде

Ф = J ( u *( r ) — u ( r )) dV —> min.

Связь действующей системы сил и получаемых перемещений описывается соотношениями p = a F + уM, ф= у TF + pM.

Перемещение любой точки зуба определяется соотношением u (r ) = p + (pxr.

Поступательное перемещение зуба будет происходить в направлении линии действия силы в том случае, если вектор силы параллелен одной из главных осей матрицы податливости при поступательном движении K ^ˆ [13]

K = ( ос-ур "‘ у T ).

На выбор величины прикладываемых сил накладываются такие ограничения, чтобы напряжения в периодонте , возникающие в результате действия данной системы сил, не превышали кровяного давления в капиллярах периодонта а*:

<з *<а, V r .

Линейно-упругая среда была смоделирована набором пружин одинаковой жесткости на растяжение и сжатие. Положение твердого тела в упругой среде при условии отсутствия нагрузки считается положением устойчивого равновесия. С помощью принципа возможных перемещений можно найти коэффициенты матриц а, у, ^у . Начальное перемещение ограничивается параметрами толщины периодонта h и малым возможным углом поворота ц. Значения величин системы сил находятся из решения критерия оптимальности. Далее они проверяются на ограничение по напряжениям из решения задачи определения напряженно-деформированного состояния периодонта методом конечных элементов.

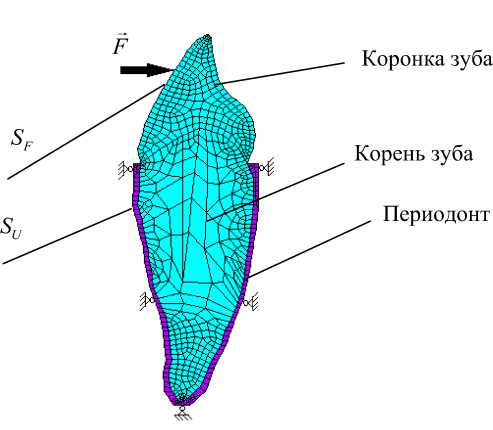
Рис. 2. Схема экспериментальной модели системы «зуб–периодонт»

Уравнения, описывающие поведение упругой среды, следующие

V6 = 0,

б = C • -8,

~   1        ТЦ—т

• 8 = — V u+Vu  .

Граничные условия выбраны следующие:

• 1.    Система ортодонтических сил осуществляется благодаря корректирующей конструкции, которая может быть прикреплена к коронке зуба FF .

• 2.    Внешняя граница периодонта считается закрепленной (данное условие моделирует соединение с костью): U|   = 0 (рис. 2).

SF

S _U

Решение задачи оптимизации начального ортодонтического ПЕРЕМЕЩЕНИЯ ЗУБА

Данная постановка была применена к задачам, моделирующим начальные перемещения зуба в трех распространенных клинических ситуациях: лечение диастемы, исправление экструзии зуба, исправление наклона зуба (рис. 3). Выбор задач обосновывается тем, что решение каждой из них достигается простейшими движениями (поступательное перемещение, чистое вращение), для которых существуют рекомендательные значения сил, полученные экспериментальным путем (см. таблицу), для сравнения с результатами решения задачи.

Лечение диастемы

Лечение диастемы заключается в устранении промежутка между двумя первыми верхними резцами. Для обеспечения подобного перемещения необходимо, чтобы линия действия равнодействующей ортодонтических сил, развиваемых корректирующей конструкцией, проходила через центр сопротивления, вызывая поступательное перемещение. Ввиду того что сила может быть приложена только к коронке зуба, доступ к центру сопротивления зуба обеспечивается благодаря принципу параллельного переноса силы. Координатные оси направим вдоль главных осей матрицы K, тогда для обеспечения необходимого направления движения зуба нужно приложить силу, параллельную оси Ox . Критерий оптимальности (1) в данном случае принимает вид

( x *- a_n ^ . )² —> min.

а                             б                          в

Рис. 3. Изображение аномалий: а – диастема; б – экструзия; в – конвергенция

При подставлении индивидуальных значений толщины x * h 0, 2 мм и податливости периодонта a 0,153 мм/Н величина силы получается равной F x 130 гc.

Исправление экструзии зуба

Рассматривается ситуация, когда зуб недостаточно погружен в альвеолярный отросток. Необходимо его погрузить, поступательно перемещая вдоль продольной оси, избежав поворота. Также прикладывается равнодействующая системы сил к центру сопротивления. Координатные оси направляются вдоль главных осей матрицы K ^ˆ , тогда для обеспечения необходимого направления движения зуба надо приложить силу, параллельную оси Oy . Критерий оптимальности (1) в данном случае принимает вид

( y * 22 F y )² min.

При подставлении индивидуальных значений толщины y * h 0, 2 мм и податливости периодонта ос 22 0, 42 мм/Н величина силы получается равной F 47 гc.

Исправление наклона зуба

Частая зубочелюстная аномалия – наклон зуба (в результате неправильно сформировавшегося прикуса, травм, проявления синдрома Попова–Годдона, конвергенции зубов) [9]. Для его исправления осуществляется поворот зуба. Этот тип движения обеспечивается приложением пары сил, приводя тело к вращению вокруг центра сопротивления. В данном случае критерий оптимальности (1) принимает следующий вид:

(ф* -р M )² min .

При подставлении индивидуальных значений поворота зуба на малый угол ф*= ц = 0, 035 рад и податливости периодонта р₃₃ 0, 0786 рад/Н∙мм величина момента пары сил получается равной M 44 гc/мм.

Ниже (рис. 4) представлены результаты решения задач по определению напряженно-деформированного состояния периодонтальной связки методом конечных элементов в пакете ANSYS.

Сравнивая полученные значения сил и момента пары сил со значениями экспериментальными (см. таблицу) для соответствующих типов перемещения зуба, можно сказать, что величины лежат в близких пределах.

Что касается удовлетворения данных силовых значений ограничению (2), то это условие выполняется лишь для второй ситуации (исправление экструзии). Для двух остальных ситуаций пиковые значения напряжений ˆ превышают допустимые не больше чем в 1,4 раза, а общий «фон» находится в приемлемых границах. Также можно сказать, что значение a* 26 гр/см2 не является эталоном, на который надо ориентироваться при лечении отдельного пациента, у каждого оно является индивидуальным.

а

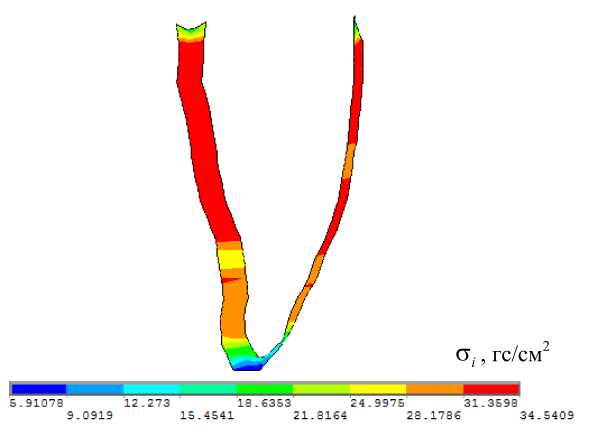
б

в

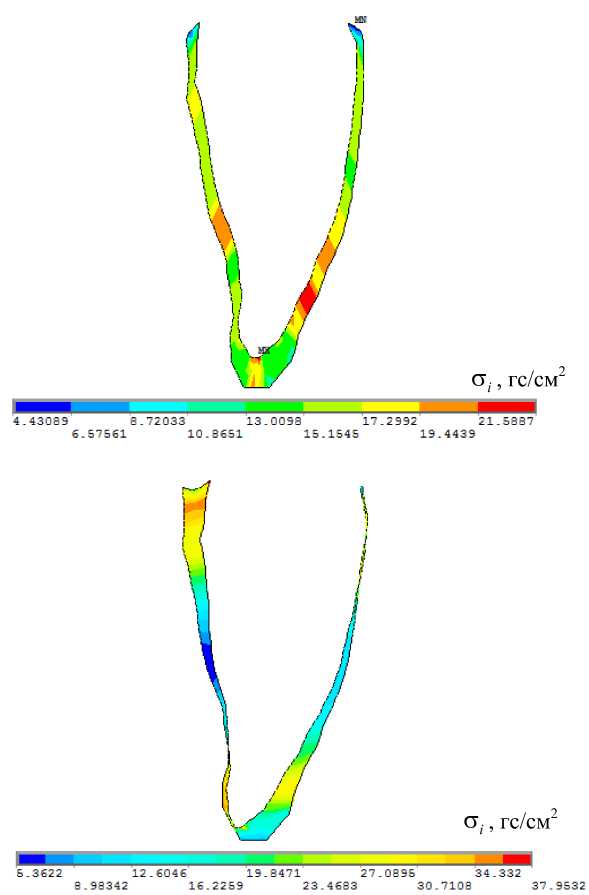
Рис. 4. Распределение напряжений в периодонте (гр/см2): а – соответствует задаче о лечении диастемы; б – соответствует задаче об исправлении экструзии;    в – соответствует задаче    об    исправлении наклона зуба

Выводы

• 1.    Предложена математическая    постановка задачи    оптимизации

• 2.    Для трех примеров, соответствующих клиническим ситуациям, были получены решения поставленной задачи. Определены величины сил и моментов пары сил, а также направление вектора равнодействующей системы сил и место его приложения для обеспечения запланированного перемещения зуба.

ортодонтического перемещения зуба с использованием понятия центра сопротивления. Введен критерий оптимизации.