Оптимизация остаточного прогиба круглой пластинки из стеклующегося полимера при неравномерном охлаждении

В статье развивается предложенная ранее методика оптимизации остаточных напряжений в изделиях из стеклующихся полимерных материалов [1]. Для описания термомеханического поведения среды используется модель упругого приближения, учитывающая эффект «замораживания» деформаций при охлаждении материала и плавность релаксационного перехода, завершенность которого описывается степенью стеклования N [1, 2]. В работе [1] для иллюстрации возможностей предложенного алгоритма минимизации остаточных напряжений решена одномерная модельная задача поиска оптимального кинематического воздействия для неравномерно охлаждаемого пакета стеклующихся стержней. Настоящая статья рассматривает двумерную осесимметричную постановку с силовым воздействием, при этом форма исследуемой конструкции и режим охлаждения близки к условиям натурного эксперимента, описанного в работе [3].

В эксперименте исследовались образцы, изготовленные по следующей технологии. Отвердитель триэтаноламинтитанат нагревался до 60 ° C , затем в течение 1 часа

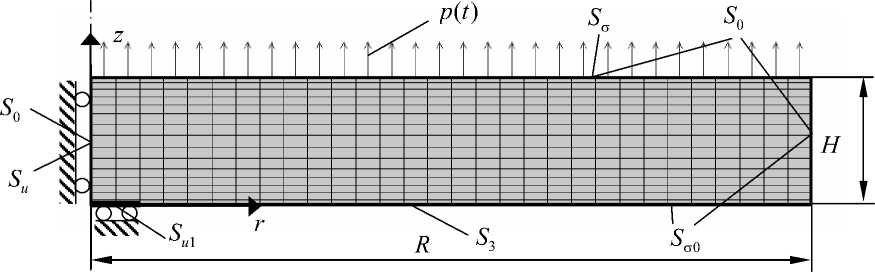
Рис. 1. Расчетная схема задачи в условиях вакуума смешивался со смолой ЭД-20 в весовой пропорции 1:10. Полученный состав заливался в форму и выдерживался в вакуумном шкафу при комнатной температуре 3 часа, после чего отверждался при 100 °C в течение 5-6 часов. Доотверждение производилось в процессе повторного нагрева до 160-170 °C и последующего охлаждения вместе с отключенным термошкафом в течение 4 часов. Из полученной таким образом цилиндрической заготовки вырезались пластины размерами H = 6 ^ 8 мм, D = 75 мм, которые затем отжигались в печи при температуре 140 °C для снятия остаточных напряжений.

Далее моделируется процесс неравномерного осесимметричного охлаждения в воде круглой пластинки из эпоксидной смолы ЭД-20 с размерами R = 37,5 мм, H = 6,5 мм (Рис. 1). В соответствии с программой эксперимента, описанного в [3], подготовленный образец нагревается до 150-170 ° C (температура, превышающая условную температуру начала стеклования T g 1 , при которой степень стеклования N ( T >  T g 1 ) = 0 [1]) и затем охлаждается путем погружения в воду нижней поверхности пластины. Результаты опыта [3] свидетельствуют, что как во время, так и по окончании охлаждения в конструкции возникают прогибы порядка 1 мм, обусловленные существенными градиентами температуры по толщине круглой пластинки.

Поставим задачу оптимизации остаточного деформированного состояния в следующей формулировке: с помощью переменного во времени силового воздействия равномерно распределенной поверхностной нагрузкой p ( t ) требуется минимизировать отклонение от плоскостности u z ( r ) = u_z ( r , H ) - u_z (0, H ) верхней поверхности образца (Рис. 1). При этом будем полагать, что взаимным влиянием дополнительного силового воздействия и температурного поля можно пренебречь (возникающие в конструкции температурные деформации пластины не изменяют значение приложенной нагрузки, а тепловыделение, обусловленное диссипацией энергии дополнительного силового воздействия, пренебрежимо мало).

Для описания термомеханического поведения материала образца воспользуемся предложенной ранее моделью упругого приближения вида [2]

N ( t )

a ( t ) = ( 4 C 1 + ⁴ C ₂ N ( t )) ••£ ( t ) - ⁴ C ₂ •• J 8 ( t ) dN ( t ) , (1) 0

где 4 C2 = 4 Cg - 4C 1; 4 Cg , 4 C 1 — тензоры упругих констант материала в стеклообразном и высокоэластическом состояниях соответственно; s(t) = 8 - sT ; s, 8T — тензоры полных и температурных деформаций соответственно;

T ( t )

s Tij = J а у(т ) dT ( т ); a _y = a5 _y ;

T 0

a — коэффициент температурного расширения; 5j — символ Кронекера; g(t) — тензор напряжений; T(t), T0 — текущая и начальная температуры соответственно; t — время. Связь между степенью стеклования N и температурой T , можно описать, например, зависимостью [2]

1 - 0,5exp

T - T g (T )

к

Tg ,

N ( T , T )

к

0,5exp

- TT - T g ( T ))

Y

к

где у — параметр, определяющий ширину интервала стеклования; T g — температура стеклования.

Для определения остаточного напряженно-деформированного состояния (НДС) конструкции с учетом сделанных допущений требуется последовательно решить две краевые задачи: задачу нестационарной теплопроводности и, на ее основе, задачу НДС.

Нестационарное температурное поле T ( x , t ) в области Ω определяется из решения задачи теплопроводности

T(x,t) = a2AT(x,t), x gQ, t g (0,t*];(3)

sup(T(x, t*)) < Tg2;(4)

x eQ

T (x,0) = To; T (x, t) = Tfn,       t > t *;(5)

X n ■ grad(T) = h (T (x, t) - Ts (t)),      x g A3;(6)

n ■ grad(T) = 0,     x g A0;(7)

где T g ₂ — условная температура конца стеклования ( N(T >  T g ₂) = 1).

В работе [1] показано, что для материалов, имеющих физические соотношения вида (1), в силу физической и геометрической линейности задачи расчета НДС, можно применить принцип суперпозиции раздельных решений «температурной» и «силовой» задач. Разобьем отрезок времени до момента окончательного охлаждения [0, t ^*] на N_t не обязательно равных частей. Под «силовой» пронимается задача определения НДС на каждом шаге по времени:

div 5a ( x , t k ) = 0 , x gQ ; (8) 5s ( x , t k ) = (( V5 u ( x , t k ))^T + V5 u ( x , t k ))/2 ; (9) 8 u ( x , t k ) ■ n ( x ) = 0, x g A u U A u, ; (10) 5o ( x , t k ) ■ n ( x ) = 5 p ( t k ) ■ n ( x ), x g A _c ; 5a ( x , t k ) ■ n ( x ) = 0 , x g A _C 0 ; (11)

_~          4^     4 ^     /   , s х А ,   .

5а ( t ) = С i + С 2 N ( T ( t k ) ) -8s ( t_k )

А     А

8s T = 0

где 8 p ( t k ) = p ( t k ) - p ( t k - 1 ) — приращение величины внешней распределенной нагрузки на к -ом шаге по времени; n ( x ) — вектор внешней нормали. Главным отличительным признаком данной постановки является учет внешнего силового воздействия при отсутствии температурных деформаций. Прямая буква «Т» в формуле (9) обозначает операцию транспоринования.

«Температурная» краевая задача также решается на каждом временном шаге и предполагает свободное (без регулирующей нагрузки p ( t )) охлаждение конструкции:

div 8°(x,tk) = 0, x eQ ;(13)

8s (x, tk) = ((V8u(x, tk)) T + V8u(x, tk))/ 2;(14)

8u(x, tk) • n(x) = 0, x e Su U Su,;(15)

8°(x, tk) • n(x) = 0, x e S° U Sco;(16)

8q(tk) = (4С + 4C2N(tk)) • •S^tk),(17)

-     ,    ,       .          T(tk )       __ где 8s = 8s - 8sT ; 8sT (tk) = j a(T)EdT, E — единичный тензор второго ранга.

T ( tk - 1 )

Остаточные напряжения и перемещения в момент полного остывания t * вычисляются в соответствии с [1] как суперпозиция «силового» и «температурного» решений:

u ( x , t * ) = u ^P ( x , t * ) + u ^T ( x , t * ),

PT

° ( x , t ) = ° ( x , t ) + ° ( x , t ).

При этом, в силу линейности задачи, каждое из слагаемых в (18) может быть определено как сумма приращений перемещений и напряжений на каждом шаге по времени от соответствующих приращений температуры и давления

Nt

N t

° ^{( x} , t ) = E⁸ ° ^{( x} , t k ); k = 1

N t

° ^{( x} , t ) = E⁸ ° ^{( x} , tk ), k = 1

u P ^{( x} , t * ) = t^{8 u} P ^{( x} , t k )> k = 1

Nt uT (x, t *)=E8uT (x, tk), k=1

где 8 u P ( x , t_k ), 8° P ( x , t_k ) — решение «силовой» задачи (8)-(12); 8 u ^T ( x , t_k ), 8° T ( x , t_k ) — решение «температурной» задачи (13)-(17).

С учетом сказанного задача безусловной оптимизации остаточных перемещений в системе, описываемой моделью (8) - (17) при наличии управляющего воздействия p ( t ) формулируется в виде:

Ф ( Р ( t ) ) = J [ F ( u T ( x , t * ) + ^u P ( x , t * )) ] dS ^ min, S c

где S_c — поверхность, на которой контролируется плоскостность образца; F ( u ) — некоторая скалярная функция вектора перемещений. В соответствии с условием задачи для контроля плоскостности образца после охлаждения выбрана осевая компонента вектора перемещений:

F ^{( u )} = u_z ^{( r} , H ).

Для конечно-элементной реализации поставленной краевой задачи используется программный комплекс ANSYS. В качестве базового выбран элемент PLANE42 с опцией осевой симметрии. Конечно-элементная сетка представлена на рисунке 1. Термомеханические свойства материала взяты из работы [5]. Теплофизические свойства в соответствии с [6] имеют следующие значения: Х = 0,19 Вт/(м К), c = 1000 Дж/(кг К), р = 1200 кг/м³.

Пространственная дискретизация в конечно-элементных расчетах сводит задачу (21) к решению системы линейных алгебраических уравнений вида [ C_p ]{ P } = { D_p } относительно вектора управляющей нагрузки P , которая имеет размерность, равную числу шагов по времени N_t . Матрица [ C_p ], как показал анализ, является плохо обусловленной, что характерно для обратных задач [7], к которым относится рассматриваемая задача. По мере увеличения числа шагов по времени растет и число обусловленности матрицы и может достигать величины, приводящей к существенной потере точности и пилообразному виду решения. При этом даже для N t <  50 , когда влияние некорректности задачи еще не столь ощутимо и остаточные перемещения удается снизить в 100 и более раз, получаемый в процессе решения уровень регулирующей нагрузки может оказаться на порядки превышающим технологически допустимый.

С целью снижения порядка разрешающей системы уравнений искомый закон распределения регулирующей нагрузки во времени далее представим в виде полинома степени N a . При условии, что в начальный момент времени ( t = 0), а также в конце охлаждения ( t = t * ) нагрузка отсутствует, выражение для p ( t ) приобретает вид

N a

Р ⁽ t ) = ⁽ t - 1) 2 ^ai t‘ , i = 1

где t = 111* — приведенное время, t e [0,1]. Тем самым задача минимизации целевой функции Ф( р ( t )) (21) относительно р ( t ) сводится к процедуре безусловной оптимизации относительно неизвестных коэффициентов a_i . После внесения первого сомножителя под знак суммы выражение (22) принимает форму:

N a

Р ⁽ t ) = 2 a i ⁽ t^{i + 1} - tⁱ ).

i = 1

Учитывая (19) и (23), получим выражение для остаточных перемещений, являющееся решением «силовой» задачи:

NtNt uP (x, 1) = Z SuP (x, tk) = Z SuP (x, tk) Apk = k=1                     k=1

N t N a                                       N t N a

= Z ^{S u} P ^{( x} , t k ) Z a ( t k ^{+ 1} - t k - l ^{1 -} t k ⁺ t k - 1 ) = Z ^{S u} P ^{( x} , t k ) Z ^{a A} t k , k = 1                    i = 1                                                k = 1                    i = 1

где S u P ( x , t_k) — решение «силовой» задачи (8)-(12) при единичном приращении внешней нагрузки A p_k = 1, A t_ik = ( t ^ ^{+ 1} - t k - 1 ¹ - t ^ + t k - 1 ). Тогда задача оптимизации (21) преобразуется к следующей дискретной форме:

N u   N t     Na          _T

Ф(а) =Z Z ^jk Z aAtxk + uTT j=1 _ k=1 i=1

^ min ,

где u j = S u P ( x j , t_k ) -S u P ( x ₀, t_k ); x j — радиус-вектор j -го узла на верхней поверхности образца (поверхности контроля плоскостности); x ₀ = {0, H }; u TT = u T ( x j ,1) - u T ( x o ,1) . После дифференцирования по неизвестным коэффициентам полинома получим систему линейных уравнений относительно коэффициентов a_i :

[ C ]{A} = {D}, где

Nu  Nt ci,=Z Z uk A tik j=1 _ k=1

Nt

Z uk A tk k=1

NuNt di =-Z uk Z uk Atik j■=1      _ k=1

( l , i = 1, N a ) .

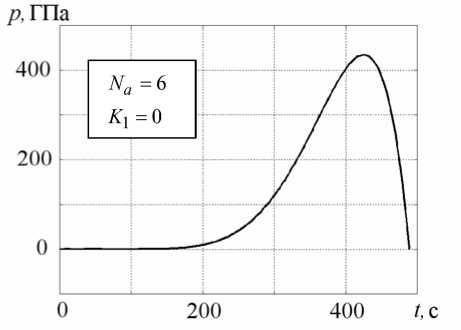
Исследование свойств матрицы [C] показало, что число обусловленности Na ц = ||C||||C 1 в норме ||C|| = max Z|cy| для значений Na от 4 до 10 равно 1018 -1030 , что примерно на 10–15 порядков меньше, чем у матрицы [Cp] в задаче (21) (в зависимости от значения Nt ). Но задача по-прежнему остается некорректной. Результаты решения согласно постановке (25) для Na = 6 приведены на рисунках 2, а и 4, а. Из рисунка 2, а видно, что оптимальная нагрузка, необходимая для поддержания остаточных перемещений на минимальном уровне, в этом случае превышает 400 ГПа, а осевые перемещения на внешнем радиусе пластины составляют 600 мм, (Рис. 3, а). Полученные значения обоих параметров находятся на неприемлемом с точки зрения практической реализации уровне. В то же время остаточные перемещения (Рис. 4, а) близки к нулю, то есть поставленная цель достигнута, однако способы ее достижения не реализуемы.

Для улучшения решения используем регуляризирующий алгоритм [7]. Введем в целевую функцию (25) дополнительный сглаживающий оператор и учтем запись регулирующей функции в виде (23):

NuNt     Na

^{ф ( а )} = Z Z u jk Z a i ^A t ik ⁺ j = 1 _ k = 1       i = 1

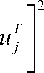
1 Г       N a

+ K i ( t ) ^eZ a i ( t

0 _        i = 1

t‘ ) dt ^ min.

Назначение дополнительного слагаемого — включение в процесс минимизации интегрального по времени уровня управляющей нагрузки, что приводит в конечном итоге к сглаживанию решения. Роль параметра регуляризации [7] в данном случае выполняет коэффициент K . При формировании второго слагаемого в выражении (27) учитывается, что для деформирования пластинки на завершающей стадии охлаждения, когда основная часть материала перешла в стеклообразное состояние, требуются более значительные усилия, нежели на начальном этапе процесса. Больший вклад управляющей нагрузки в конце охлаждения реализуется с помощью сомножителя ( t ) ^в (см. второе слагаемое в (27)). Коэффициенты K и в подбираются в зависимости от условий задачи.

С учетом дополнительного ограничения получим результирующую систему уравнений:

[ G ]{ A} = { D},                                                                       (28)

где     [ G ] = [ C ] + K [ C 1] ;

компоненты

----1--;

l + i + 2 р + 1 l + i + 2 в + 2 l + i + 2 p + 3

матрицы [ C ] и вектора { D } вычисляются по формулам (26).

Для уменьшения зависимости диапазона варьирования коэффициента K от степени аппроксимирующего полинома N_a представим этот коэффициент в виде произведения

K = K 1 K ₂, где коэффициент K ₂ определяется из условия соразмерности элементов матриц [ C ] и [ C 1 ] , входящих в уравнение (28):

K 2 =

aa

с..

ij c1ij

( Na )’

Сведение задачи оптимизации к виду (28) позволяет снизить число обусловленности на 8–10 порядков в зависимости от степени аппроксимирующего p ( t ) полинома. Таким образом, для получения приемлемого с точки зрения уровня остаточных деформаций и уровня регулирующей нагрузки решения в окончательном варианте задачи оптимизации (28) необходимо осуществлять дополнительную процедуру подбора теперь уже параметров в и K 1 .

Исходя из того, что наибольшие вертикальные перемещения, возникающие при оптимальном внешнем силовом воздействии p ( t ), на всем временном интервале охлаждения не должны превышать соответствующих величин при свободном остывании образца, запишем следующее ограничение:

max U P ( t , Р ( t ), R , H )| - max u_z^T ( t , R , H ).                                              (29)

zz t e [0, t |                                          ¹ t e [0, t ]^{1                           1}

Далее для каждого значения N a методом простого перебора находим величины в и K 1 , удовлетворяющие данному условию.

Задача оптимизации решена для следующих значений порядка полинома, аппроксимирующего функцию силового воздействия p ( t ) : N a + 1 = 5; 7; 9 . Результаты приведены в таблице и на рисунках 2–4.

Таблица. Параметры задачи оптимизации

Параметр	Порядок полинома N a + 1
	Задача без регуляризации (25)			Задача с регуляризацией (27)
	5	7	9	5	7	9
в	0	0	0	3	3	3
K 1	0	0	0	0,01	0,10	0,10
II Д u lImax	2,79	1,84	0,742	8,29	7,01	6,38
IIД U L	3,77	1,27	0,792	7,56	7,46	6,65

Параметры ||Д u\ |m _a x и ||Д u^_L характеризуют относительный уровень остаточных перемещений при оптимальном режиме нагружения в равномерной и лагранжевой нормах соответственно:

। = 100% max N

zj

0,5

;

|| Д u\\_L = max | u_z P ( t *) + u^T_2j( t *)|/ max | u T ( t *)| - 100% .

В первых трех колонках таблицы представлены результаты решения задачи без регуляризации (25). Уровень остаточных перемещений снижается более чем в 100 раз при N_a = 8 по сравнению с уровнем, полученным без оптимизации. Из анализа результатов решения (27) (последние три колонки таблицы) видно, что существенного уменьшения остаточного отклонения от плоскостности удается добиться уже при достаточно низких степенях аппроксимирующего нагрузку полинома. В частности, при N_a = 4 максимальное и среднее отклонения снижаются более чем в 10 раз. Последующий рост N_a до 8, как видно из таблицы, уменьшает уровень остаточных перемещений еще примерно на 20%. Невозможность дальнейшего снижения остаточных прогибов объясняется наличием ограничения на величину управляющей нагрузки (27), вклад которого в целевую функцию регулируется параметром K ₁ . При этом, как показано в таблице, требование удовлетворения критерию (29) приводит к росту K ₁ в 10 раз для N_a , равных 6 и 8. Увеличение степени полинома улучшает результаты, что косвенно свидетельствует о сходимости решения

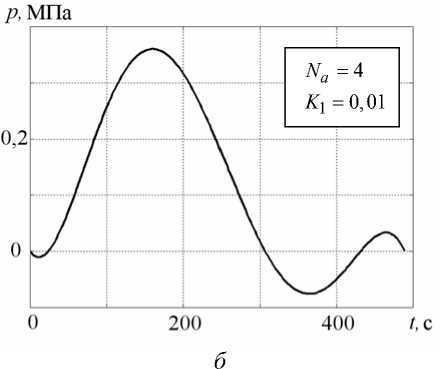
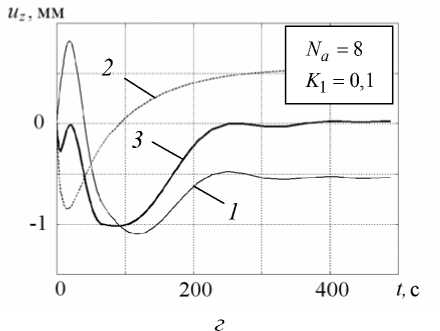
Вид оптимальной управляющей нагрузки для задачи (27) при различных значениях N_a показан на рисунке 2, б – г . На всех графиках наблюдается отрицательный экстремум в момент времени t * 10 с. Его наличие, с точки зрения механики, объясняется необходимостью компенсации начального температурного прогиба образца при охлаждении нижних слоев материала (см. участок 0–10 с на кривых 2 рисунка 3, б – г ). На данном промежутке времени регулирующая нагрузка действует практически синхронно прогибу, но в противоположном ему направлении (отрицательный знак p соответствует отрицательному давлению на поверхность 5 _с , (Рис. 1)). Наибольшее положительное давление, как видно из рисунка 2, б – г , реализуется на временном интервале 100–150 с, когда значительная часть материала пластины еще находится в высокоэластическом

а

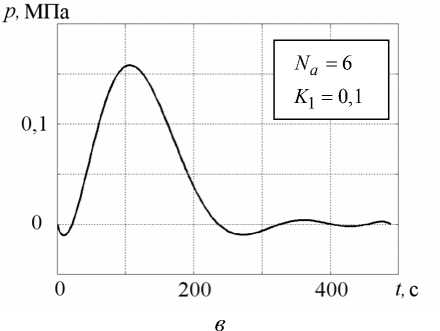
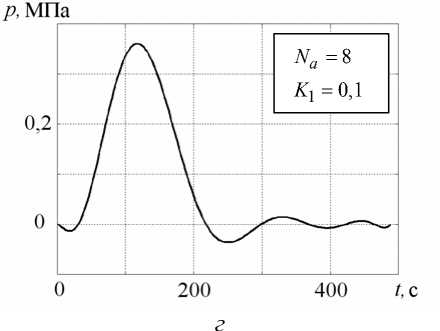
Рис. 2. Зависимость оптимальной управляющей нагрузки от времени

состоянии, но изгибная жесткость существенно больше, чем на начальной стадии охлаждения. Отсюда следует рост уровня давления, компенсирующего стремление свободной от нагрузки пластины прогнуться в обратном направлении при t = 100 - 500 с. (кривые 2 на рисунке 3, б – г ).

Графики перемещений под нагрузкой без учета температурных деформаций u_z^P ( t ) (кривые 1, Рис. 3, б – г ) показывают сходимость решения к устойчивой форме с двумя доминирующими экстремумами — максимумом при t ® 10 с и следующим за ним минимумом при t « 100 с. В результате на суммарном графике перемещений охлаждаемого образца, подверженного оптимальному силовому воздействию (кривые 3, Рис. 3, б – г ), существенно снижен начальный пик перемещений u_z^T ( t ), наблюдаемый при свободном охлаждении (кривая 1, Рис. 3, б - г ). В интервале до t * 70 с отрицательный прогиб образца растет до максимума порядка 1 мм с последующим уменьшением практически до нуля в течение ~200 с.

На рисунке 4, б – г представлены профили остаточного прогиба верхней поверхности образца после свободного охлаждения (кривые 1 ) и охлаждения с регулирующим силовым воздействием p ( t ) (кривые 2 ). Сравнение кривых показывает, что, начиная с N a = 4, форма остаточного прогиба не изменяется и максимальные остаточные перемещения при этом уменьшаются, но незначительно (в 1,13 раз).

Введение регуляризирующего слагаемого в целевую функцию требует анализа влияния параметра регуляризации на качество решения для обоснования выбора значения коэффициента K ₁ . На рисунке 5 приведены графики зависимости от этого

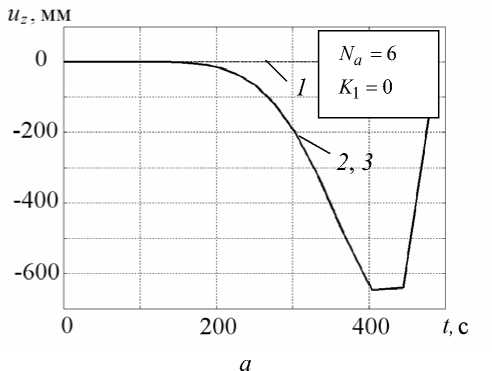
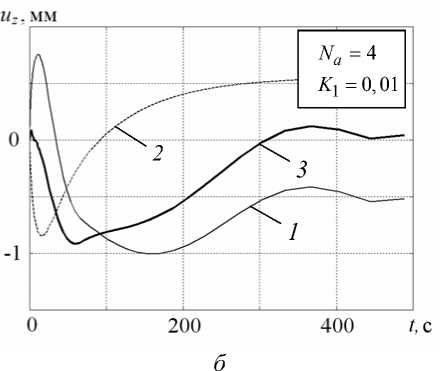
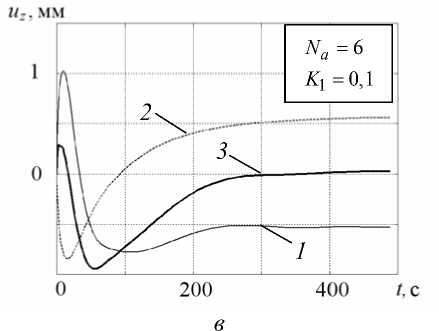
Рис. 3. Зависимость от времени перемещений u_z в точке r = R , z = H : кривые 1 - u P ( t ); 2 - u j ( t ); 3 - u j ( t ) + u P ( t )

параметра двух основных характеристик оптимизации — максимального значения управляющей нагрузки и наибольшего удельного остаточного отклонения от плоскостности. Из рисунка видно, что увеличение вклада сглаживающего слагаемого в (27) приводит к снижению p _max с одновременным повышением уровня остаточных перемещений. Кроме того, влияние K ₁ зависит от степени аппроксимирующего полинома (с ростом N_a графики смещаются вправо). Приведенными диаграммами можно пользоваться для поиска приемлемого решения. Например, при предельно допустимом значении управляющего давления [ p max ] = 1МПа для N a = 8 (кривая 3 , Рис. 5, а ) определяется lg K 1 =- 1,8. По графику рисунка 5, б данному значению коэффициента отвечает ||Д u | |max = 5%, что соответствует снижению остаточных перемещений примерно в 20 раз по сравнению с перемещениями, полученными без внешнего силового воздействия. Уменьшение уровня допустимых усилий в 10 раз при прочих равных условиях вызывает рост остаточных перемещений (||Д u ||max = 7,5%).

Следует также отметить наличие участков «стабильности» уровня остаточных перемещений. Например, в интервале lg K 1 е [ - 3,0] значение ||Д u ||max практически постоянно для N a = 6 (кривая 2 , Рис. 5, а ), в то время как величина P_max в данном диапазоне меняется почти на порядок. Рост степени полинома при прочих равных условиях снижает уровень остаточных деформаций. В частности, при

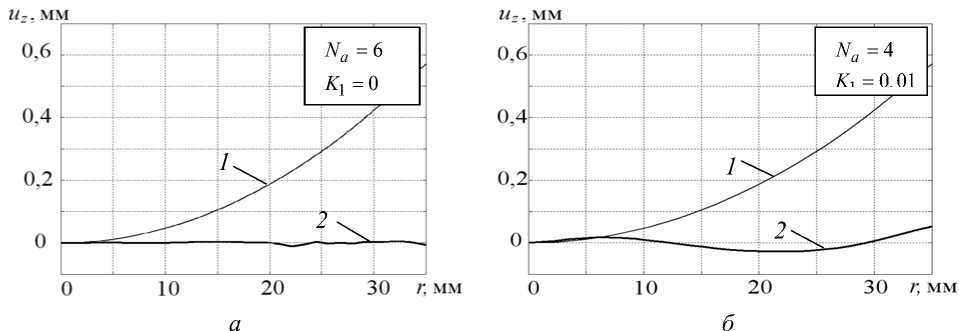
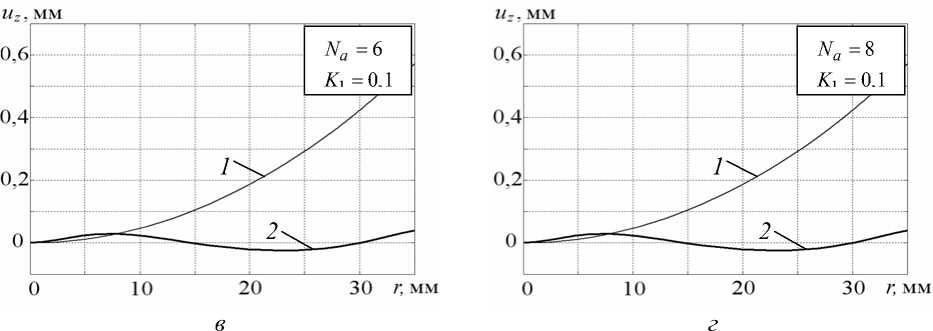
Рис. 4. Распределение остаточных перемещений u_z по радиусу ( z = H ): криваые 1 — u T ( t * ); 2 — оптимальное распределение u T ( t * ) + u P ( t * )

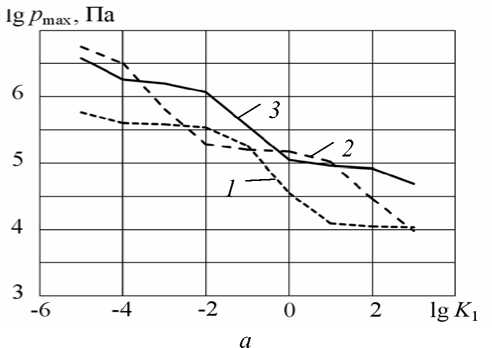
Рис. 5. Максимальное управляющее давление ( а ) и остаточное отклонение от плоскостности ( б) в зависимости от параметра регуляризации при различных значениях порядка полинома N a :

4 (кривые 1 ); 6 ( 2 ); 8 ( 3 )

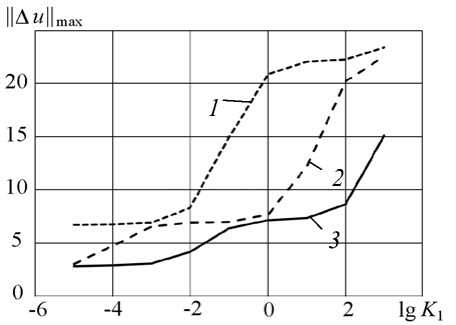
ограничении [ p _max] = 0,1 МПа можно достичь снижения ||Д u ||_m ax до 17,5%, 12,5%, 7,5% от первоначального уровня при значениях N_a , соответственно равных 4, 6 и 8.

Таким образом, поставлена и решена задача минимизации остаточных перемещений в круглой пластинке из материала с термомеханическими свойствами, описываемыми моделью (1). Показано, что в рамках принятых ограничений, упрощающих вид управляющего воздействия, а также учитывающих линейность физических соотношений, можно существенно уменьшить объем расчетов, сводя задачу безусловной оптимизации к решению системы линейных уравнений, коэффициенты которой вычисляются однократным решением двух прямых задач. Для численной реализации прямой краевой задачи термомеханики применен метод суперпозиции пошаговых решений задач термоупругости, выполняемых в конечно-элементном пакете ANSYS. Предложенная методика сглаживания функции управляющей нагрузки позволяет получить ощутимое снижение уровня остаточных перемещений пластинки с учетом ограничения по величине управляющего воздействия путем варьирования параметра регуляризации, оставаясь в рамках линейной задачи.

Предметом дальнейших исследований должно стать строгое доказательство существования и единственности оптимального решения, анализ возможности и целесообразности применения предложенной методики к различным видам конструкций, а также включение в постановку задачи классических ограничений в виде неравенств.