Оптимизация параметров сигмоидальной функции при моделировании сигналов пцр в реальном времени

ВВЕДЕНИЕ                   жет быть выражена в следующем виде:

F = F m / (1+exp (( С 0 – C ) / k )) +

Первым шагом при обработке сигналов анали заторов нуклеиновых кислот методом полимераз-              + f0 + f1 · C + f2 · C ,             (1)

ной цепной реакции в реальном времени (ПЦР-РВ) при относительных количественных измерениях является определение пороговых циклов (далее — C t ), при которых сигналы флуоресценции образцов достигают постоянного уровня, выбранного оператором. Высокая воспроизводимость определения пороговых циклов (среднеквадратичное отклонение менее чем 0.2 циклов) [1] позволяет сравнивать концентрацию исследуемых и калибровочных образцов [2]. При этом используется основное свойство ПЦР — рост сигналов на начальной стадии реакции происходит по экспоненциальному закону. В статье [3] был выполнен практический анализ погрешностей определения C t путем расчета значений стандартного отклонения пороговых циклов. При малых объемах реактивов, которые экономически выгодны при выполнении массовых анализов, возникает необходимость изучения влияния шумов и дрейфа нулевой линии детектора на погрешности количественных измерений. В статье [4] было выполнено сравнение разных способов определения C t . В настоящей статье предложена усовершенствованная модель для обработки сигналов на основе сигмоидальной (S-образной) функции (СФ) [5] и показана возможность практически полного устранения влияния дрейфа детектора.

АНАЛИТИЧЕСКАЯ ФОРМА СИГМОИДАЛЬНОЙ ФУНКЦИИ

Кинетическая модель сигналов ПЦР-РВ на базе нелинейной сигмоидальной функции (МСФ) мо- где F — интенсивность флуоресценции реакции при порядковом номере цикла амплификации С; Fm — максимальная интенсивность флуоресценции в конце реакции; С0 — дробный цикл, при котором интенсивность флуоресценции достигает половины значения Fm; k — коэффициент, который определяется наклоном кривой; f0 — смещение нулевой линии (фон детектора).

Традиционное выражение МСФ [3] дополнено нами еще двумя слагаемыми:

f 1 · C + f 2 · C ².

Коэффициент f 1 определяется линейным дрейфом нулевой линии, а коэффициент f 2 учитывает квадратичную составляющую дрейфа нулевой линии. Необходимость дополнительных слагаемых возникает в случаях, когда с целью экономии используются малые объемы реактивов, при этом интенсивность флуоресценции реакции становится соизмеримой с дрейфом нулевой линии.

Целью построения МСФ является уменьшение погрешности вычисления порогового цикла.

МЕТОДИКА ПОСТРОЕНИЯ И ОПТИМИЗАЦИИ ПАРАМЕТРОВ МСФ

С помощью электронной таблицы Excel можно построить и оптимизировать параметры МСФ (табл. 1).

В ячейках С4:С9 табл. 1 заданы исходные параметры модели. В терминах Excel интенсивность флуоресценции в ячейке С11 вычисляется следующим образом:

Табл. 1 . Электронная таблица для вычисления параметров МСФ

	A	B	C	D	E	F
1
2		Порог =	500
3		C t =	23,500
4		C 0 =	23,5
5		F m =	1000
6		k =	1,39
7		f 0 =	0
8		f 1 =	0
9		f 2 =	0
10	С=	S =	0
11	1	9,33E-05	9,33E-05	0	9,33E-05	0
24	14	1,07	1,07	0	1,07	0
33	23	411,029	411,029	0	411,029	0
34	24	588,971	588,971	0	588,971	0
43	33	998,9	998,9	0	998,9	0
60	50	1000	1000	0	1000	0

С11 =$С$5/(1+EXP(($С$4-А11)/$С$6))+ $С$7+ $С$8*А11+$С$9*(А11)^2 ,

где порядковый номера цикла С = 1 приведен в ячейке A11. Полностью МСФ строится в ячейках С11:С60 как зависимость от номера цикла, записанного в ячейках А11:А60 = 1÷50.

В ячейках В11:В60 можно расположить полученную на анализаторе ПЦР зависимость флуоресценции от номера цикла в числовом выражении, желательно нормированную при F m = 1000 и f 0 = 0 о.е. (относительных единиц). Ячейки D11:D60 можно использовать для имитации дрейфа нулевой линии детектора и других видов помех. В ячейках E11:E60 вычисляются суммы (В11+D11):(В60+D60). В ячейках F11:F60 получаются квадраты разностей (Е11– С11)²:(Е60 – С60)², а в ячейке С10 — остаточная сумма квадратов разностей S .

Оптимизация параметров модели выполняется путем использования инструмента Поиск решения из меню Сервис . Для этого необходимо выполнить следующий набор команд:

– "Установить целевую ячейку" – С10 – " Равной: минимальному значению" – " Выполнить" – " Изменяя ячейки" – С4:С9 .

В результате в ячейках С11 : С60 получаются чи- словые значения зависимости оптимизированной модели от номера цикла, а в ячейках С4:С9 — новые параметры МСФ. Модель получается оптимизированной по методу наименьших квадратов ошибок.

В приведенном примере в ячейки В11:В60 внесена численная копия исходной нормированной МСФ из ячеек С11:С60, поэтому после выполнения вычислений параметры модели остались прежними.

Традиционно уровень порога выбирается оператором на участке экспоненциального роста флуоресценции [1]. Экспоненциальный участок может быть определен, как линейная часть графика сигнала флуоресценции на логарифмической шкале. На рис. 1 приведены почти полностью совпадающие графики реального сигнала и модели после нормировки ( F m = 1000 и f 0 = 0 о.е.). Для определения пороговых циклов C t в статье [4] был рекомендован уровень порога, равный 500 о.е. При таком уровне обеспечивается минимальное влияние шумов детектора на погрешности измерения, этот уровень условно можно считать концом участка экспоненциального роста флуоресценции (при линейном масштабе — это точка перегиба).

Дробный цикл С 0 удобно принять в качестве величины порогового цикла C t реального сигнала

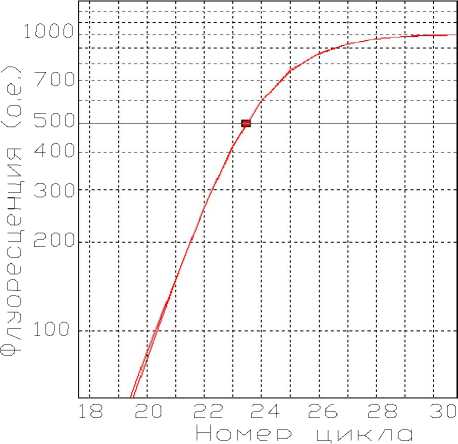
Рис. 1. Графики сигнала и модели после нормировки

ПЦР. Условие C t = C 0 выполняется, если выбрать уровень порога, при котором интенсивность флуоресценция достигает половины значения F m (в этом примере F m /2 = 500 о.е.).

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ДРЕЙФА НУЛЕВОЙ ЛИНИИ ДЕТЕКТОРА

С помощью электронной таблицы Excel выполнен численный эксперимент, результаты которого доказывают, что даже при неблагоприятных условиях c помощью МСФ удается устранить влияние дрейфа нулевой линии.

Для имитации дрейфа нулевой линии детектора формировались числовые последовательности f 0 , f 1 · C , f 2 · C ² и f 3 · C ³ с величинами коэффициентов f 0 = 100 о.е., f 1 = 2 о.е., f 2 = 0.04 о.е. и f 3 = 0.0008 о.е. При таких коэффициентах максимальное отклонение нулевой линии составляет 100 о.е., т. е. 10 % от максимальной нормированной интенсивности флуоресценции в конце реакции F m = 1000 о.е. Дополнительно формировалась числовая последовательность суммы f 0 + f 1 · C + f 2 · C².

Числовые последовательности поочередно вносились в ячейки D11:D60. При этом в ячейках Е11:Е60 выполнялось суммирование исходной нормированной сигмоидальной функции с числовой последовательностью, имитирующей дрейф нулевой линии детектора, а в ячейке С10 получалась новая сумма квадратов разностей S .

После выполнения действий по оптимизации параметров модели (с целью получения минимального значения S ) в ячейках С11:С60 получаются числовые значения зависимости новой оптимизированной модели от номера цикла. Новые параметры МСФ в ячейках С4:С9 приведены в табл. 2.

Сравнивая полученные в табл. 2 параметры (выделены жирным шрифтом) с заданными параметрами ( f 0 = 100, f 1 = 2, f 2 = 0.04 о.е.), можно сделать вывод о хорошем совпадении параметров моделей и исходных последовательностей с дрейфом нулевой линии. Особенно ценным качеством модели с предложенными дополнительными параметрами является малая зависимость от дрейфа величины C 0 , которую можно принять в качестве порогового цикла. Даже при дрейфе нулевой линии, который характеризуется кубической зависимостью, величина C 0 отличается от исходной величины менее чем на 0.5 % амплификационного цикла.

Табл. 2 . Результаты вычисления параметров МСФ

Параметры МСФ	Исходные значения параметров	Имитация дрейфа нулевой линии детектора
		f 0 = = 100 о.е. (макс.)	f 1 · C = = 100 о.е. (макс.)	f 2 · C 2 = = 100 о.е. (макс.)	f 0 + f 1 · C + + f 2 · C 2 = = 300 о.е. (макс.)	f 3 · C 3 = = 100 о.е. (макс.)	f 3 · C 3 = (от 14 до 33 циклов)
C 0	23.5	23.499	23.499	23.500	23.500	23.496	23.500
F m	1000	999.997	999.988	999.988	999.989	988.441	998.215
k	1.39	1.390	1.390	1.390	1.390	1.371	1.389
f 0	0	99.999	–2.003	0.038	98.038	2.728	8.024
f 1	0	0.000118	2.0004	–0.083	1.917	–0.900	–1.241
f 2	0	–4.5E–07	–1.7E–06	0.042	0.042	0.060	0.057
S	0	2.07E–05	0.00016	0.00015	0.0002	49.041	0.010
R 2	1	1	0.9994	0.9990	0.9973	0.9986	1

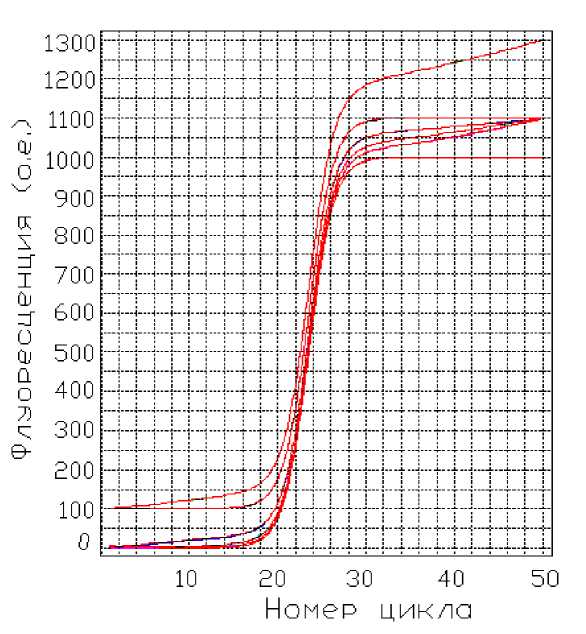
Рис. 2. Графики сигналов и моделей

После завершения ПЦР, результатом которой является быстрый рост сигнала флуоресценции, может наблюдаться медленное увеличение или уменьшение сигнала флуоресценции. Этот эффект подобен дрейфу нулевой линии, хотя имеет другую причину. Уменьшить влияние этого эффекта можно путем использования укороченной модели сигмоидальной функции (УМСФ). Приведенная в ячейке В24 табл. 1 интенсивность модельного сигнала при 14-м цикле отличается от нуля примерно на 1 о.е., а интенсивность модельного сигнала при 33-м цикле (В43) отличается от максимального значения (1000 о.е.) также примерно на 1 о.е. Поэтому при допустимой погрешности интенсивности сигнала около 0.1 % можно применить УМСФ в интервале от 14 до 33 циклов. Результаты вычисления основных параметров ( C 0, k и R ²) УМСФ при дрейфе нулевой линии с кубической зависимостью, приведенные в крайнем правом столбце табл. 2, мало отличаются от исходных параметров.

При использовании УМСФ можно сократить время, затраченное на выполнение ПЦР, если не регистрировать сигналы флуоресценции в течение нескольких первых циклов.

Для использования в качестве иллюстрационного материала можно построить упрощенные модели, используя данные табл. 1 с вновь вычисленными параметрами C 0 и k при F m = 1000 о.е. и величинами f 0 , f 1 , f 2 , равными нулю.

Критерием приближения прогнозируемой модели к исходной фактической последовательности может служить остаточная сумма квадратов разностей S. В безразмерной форме функциональную близость можно оценить с помощью квадрата коэффициента корреляции R ² (функция Excel КВПИРСОН ). Вычисленные значения этих критериев приближения приведены в табл. 2. Степень приближения можно считать очень высокой, если величина R ² более 0.99.

Подобная методика построения МСФ реализована при модернизиации программного обеспечения анализатора нуклеиновых кислот АНК-32, который серийно выпускается в ИАП РАН [6]. Сигналы, имитирующие дрейф нулевой линии детектора (максимальное отклонение — до 300 о.е.), вводились в программу обработки информации в виде текстового файла. На рис. 2 одновременно изображены графики введенных сигналов и графики МСФ. Можно отметить почти полное попарное совпадение этих графиков. Различие величин С 0 всех графиков не превышает 1 % порогового цикла.

В модернизированном программном обеспечении реализована нормировка (привязка графиков к нулю и к максимальному значению), а также выполняется коррекция наклона нулевой линии. Все эти операции выполняются в ручном и автоматическом режимах.

ВЫВОДЫ

Предложена усовершенствованная модель сигналов ПЦР-РВ и методика оптимизации ее параметров на основе одного из наиболее эффективных способов обработки сигналов — способа аппроксимации с помощью сигмоидальной функции.

При определении порогового цикла предложено выбирать уровень порога, при котором интенсивность модельного сигнала достигает половины значения максимальной интенсивности в конце реакции. Выполнен численный эксперимент, результаты которого доказывают, что даже при неблагоприятных начальных условиях при таком выборе уровня порога удается устранить влияние дрейфа нулевой линии на результаты моделирования. Рассмотрены преимущества использования укороченной модели сигмоидальной функции.

Приведены критерии приближения прогнозируемой модели к фактическому росту интенсивности сигналов флуоресценции в ходе реакции.

Показана возможность полной автоматизации вычислений пороговых циклов сигналов ПЦР-РВ.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках федеральной целевой программы "Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007– 2012 годы" при выполнении научно-исследовательской работы по лоту (шифр 2011-1.2-512-073) "Разработка макетов аппаратно-программных комплексов для лабораторной и функциональной диагностики" по теме: "Разработка макета аппаратно-программного комплекса для лабораторной и функциональной диагностики широкого спектра признаков методом полимеразной цепной реакции в реальном времени" (шифр заявки 2011-1.2-512-073-110).