Оптимизация параметров технологического трубопровода по технико-экономическим показателям

При создании предприятий пищевой промышленности одним из наиболее важных и сложных этапов является проектирование и расчет технологических трубопроводов. На выполнение этого этапа затрачивается до 30–35% от общих трудозатрат на разработку технологической и монтажно-технологической частей проекта.

С позиций системного анализа технологические трубопроводы представляют собой функциональную подсистему, в которой осуществляются взаимосвязанные между собой гидравлические, тепловые и механические процессы и явления, интегрированную в общую химикотехнологическую систему и обеспечивающую практическую взаимосвязь между отдельными единицами технологического оборудования [1].

Основными элементами системы технологических трубопроводов являются технологические трубопроводы, машины для создания разности давлений (насосы, компрессоры) и технологические резервуары [2].

Технологические трубопроводы классифицируют по различным признакам: виду транспортируемой среды, материалу, применяемому для изготовления, длине, величине давления, функциональному назначению, наличию и типа тепловой изоляции, способу прокладки [1, 2].

Проектирование новых технологических трубопроводов и модернизация действующих трубопроводных систем представляет собой комплексную организационно-техническую задачу [1], одним из этапов которой является проведение гидродинамических расчетов на основе уравнений неразрывности и Навье-Стокса, дополненных уравнениями конвективной теплопроводности и состояния движущейся среды, что представляет известные трудности.

Используя допущения об изотермичности, стационарности и несжимаемости потока движущейся среды, задачу в исходной постановке сводят к проведению гидравлических расчетов по уравнению неразрывности потока и уравнению Бернулли для реальной вязкой жидкости, которое учитывает потери давления на трение и на преодоление местных сопротивлений трубопровода. Данный подход является общепринятым в отечественной и зарубежной практиках при проведении гидравлических расчетов технологических трубопроводов пищевых и химических производств и охватывает решение трех практических задач: определение диаметра трубопровода, определение перепада давления в трубопроводе и оценка его пропускной способности [2, 3].

Для расчета технологических трубопроводов транспортировки неньютоновских пищевых сред традиционные методики уточнены эмпирическими соотношениями, позволяющими учесть аномалию вязкости перекачиваемого продукта [4, 5].

Гидравлические расчеты сложных трубопроводов с разветвлениями, кольцами, участками разного диаметра и пр. проводят с использованием методов теории графов и электрогидравличе-ской аналогии [1, 6].

Возможности численного моделирования трубопроводных систем сложной структуры позволяют рассматривать тепломассообменные, химические и биохимические процессы, протекающие в трубопроводных системах, взаимосвязанными, моделировать режимы работы и выбирать оптимальные конструктивные и эксплуатационные параметры [7–12].

Одной из задач при традиционном гидравлическом расчете является задача определения диаметра трубопровода и потерь давления в линии заданной трассировки при постоянном объемном расходе [2].

При таком подходе гидравлический расчет является многовариантной задачей, т. к. существует бесконечное множество сочетаний параметров диаметр трубопровода – перепад давления, обеспечивающих перекачивание транспортируемой среды с заданным расходом.

Причем варианты неравноценны как с экономической, так и технической точки зрения.

Так, с одной стороны, при уменьшении диаметра трубопровода снижается его стоимость и металлоемкость (т. е. капитальные затраты), но, при заданном расходе жидкости, увеличивается скорость ее течения, и, как следствие, возрастают потери давления на ее перекачивание по трубопроводу. Для создания более высокого давления в трубопроводе требуется установка более мощного гидравлического насоса, потребляющего больше электроэнергии. Следовательно, снижение капитальных затрат на создание трубопроводной системы путем уменьшения диаметра трубопровода приводит к удорожанию стоимости насосной установки и затрат на эксплуатацию трубопроводной системы.

С другой стороны, транспортирование жидкости по более дорогому трубопроводу, изготовленному из труб большего диаметра, требует меньших затрат электроэнергии на привод насосной установки.

В этой связи выбор диаметра трубопровода должен быть обоснован как технически, так и экономически. Очевидно, существует некий оптимальный диаметр трубопровода, при котором сумма затрат на сооружение технологического трубопровода и перекачивания по нему жидкости будет минимальной.

Для решения такой задачи оптимизации предложено большое количество техникоэкономических критериев, отличающихся друг от друга сложностью, детализацией и количеством учитываемых экономических и технологических показателей. Однако общим для всех критериев является учет эксплуатационных затрат, связанных с затратами на электроэнергию для привода насоса (затраты на создание перепада давления) и капитальных затрат, обусловленных стоимостью трубопровода [13, 14].

В качестве примера можно отметить работы [15-18], где в качестве критерия оптимизации использован показатель совокупных дисконтированных затрат. В работах [19-21] приведена оптимизация параметров трубопровода по затратам электроэнергии на привод насоса. При оптимизации параметров криогенных трубопроводов в качестве критериев оптимизации авторы [22, 23] использовали мощности гидравлических и тепловых потерь. Использование метода исследования пространства параметров (МПП) позволило авторам найти Парето-оптимальное решение. Для минимизации мате-риалозатрат на воздуховоды вентиляционных систем авторами [24-26] использовано динамическое программирование, позволившее последовательно определить оптимальные диаметры участков вентиляционной системы для заданных значений давлений и расходов воздуха. В работе [27] предложен выбор оптимального диаметра трубопровода для сети централизованного теплоснабжения, состоящей из ответвлений и колец, с использованием теории графов и минимизации затрат.

В этой связи актуальной является задача определения оптимального диаметра и потерь давления в трубопроводе, обеспечивающих одновременно снижение стоимости трубопровода и затрат электроэнергии для привода насоса.

Объекты и методы

В качестве критерия технико-экономической оптимизации (ТЭО) используем суммарные годовые затраты F , р./год на создание и эксплуатацию технологического трубопровода, являющиеся линейной суперпозицией капитальных K , р., и эксплуатационных Э , р., затрат [13, 14]

F = K + Э .            (1)

Капитальные затраты K , р./год, в первом приближении, представим как затраты на создание трубопровода, пропорциональные его габаритным размерам, прейскурантной цене и отнесенные к одному году эксплуатации трубопровода

K = Ц ( D ) L ,          (2)

где L - общая длина трубопровода (включает в себя длину всех горизонтальных и вертикальных участков), м; f mp ( D ) - регрессионное уравнение, аппроксимирующее прейскурантные данные по стоимости трубопровода в зависимости от его диаметра. Величина f mp ( D ) является стоимостью 1 погонного метра трубопровода диметром D и толщиной стенки трубы 5 , мм.

В качестве аппроксимирующей функции fmp(D) в [1] рекомендуется линейная зависимость fmp (D) = aD ,            (3)

где a - регрессионный коэффициент, р./м²; D диаметр трубопровода, м.

С учетом (3) капитальные затраты по формуле (2) представим в виде к = SdD ,             (4)

где S D - удельные затраты, р./м

S_D = aL .               (5)

Эксплуатационные затраты Э, р./год, на эксплуатацию трубопровода в течение календарного года представляют собой затраты на перемещение среды по трубопроводу и пропорциональны количеству электроэнергии, потребленной насосом за время его работы в течение года и тарифной стоимости 1 кВт-ч электроэнергии

Э = 365 N^ r ,        (6)

где N эл - мощность электродвигателя привода насоса, кВт; с_эл - тариф (стоимость) 1 кВт - ч электроэнергии, руб./кВт - ч; т - продолжительность работы трубопроводной установки в течение суток, ч.

Мощность электродвигателя привода насоса

N = K_з

Q Δ P

1000 7 п

где К з - коэффициент запаса мощности электродвигателя К з = 1,2; Q - объемный расход транспортируемой среды, м³/с; А Р - давление, развиваемое насосом, Па; п - КПД привода насоса (учитывает механический КПД, утечки через зазоры и сальники насоса, износ и пр.), П = 0,8.

С учетом (7) эксплуатационные затраты по формуле (6) представим в виде

Э = 5p АР,(8)

где S_P - удельные затраты для создания единицы перепада давления, руб./кПа

Sr = 365К,QV .(

η

С учетом затрат (4) и (9) критерий оптимизации по формуле (1) примет вид [28]

F = SP АР + SdD .(10)

В критерии (10) давление А Р , развиваемое насосом, представляет собой потери давления в технологическом трубопроводе, зависящие от его топологии, наличия гидравлических сопротивлений, объемного расхода транспортируемой жидкости и ее свойств, а также диаметра трубопровода [2]. Таким образом, критерий ТЭО (10) учитывает текущие значения цен и тарифов на трубопровод и электроэнергию, параметры трубопровода, условия транспортирования жидкости, ее свойства и отвечает основным требованиям, предъявляемым к критериям оптимизации [1]: измеряет эффективность системы; является количественным; имеет ясный физический смысл и достаточно полно отражает наиболее существенные стороны процесса.

Задача технико-экономической оптимизации технологического трубопровода заданной топологии заключается в нахождении таких значений D и АР, при которых критерий ТЭО (10) достигает минимального значения при заданном объемном расходе транспортируемой среды Q, который, в свою очередь, также зависит от D и АР [31]:

F ( А Р , D ) = S p А Р + S d D   ^ , D >  min ,   (11)

Q ( А Р , D ) = const .         (12)

Таким образом, имеем задачу условной оптимизации критерия (11) при наличии ограничения (уравнения связи) вида (12). Для решения задачи в постановке (11) и (12) необходимо свести ее к задаче на безусловный экстремум.

Уравнение связи (12) должно в явном виде связывать потери давления Δ P , диаметр трубопровода D и объемный расход Q транспортируемой среды.

Представим связь между А Р и D в виде уравнения

А Р = А Р +А Р ±А Р ,      (13)

лин       мс       гс , где АРлин - потери давления по длине трубопровода, Па; АРмс - потери давления, обусловленные наличием местных сопротивлений, Па; АРгс - гидростатические потери давления, связанные с изменением высоты подъема (опускания) транспортируемой среды, Па.

Потери давления по длине трубопровода определим по формуле Дарси-Вейсбаха

А Р = X L ⁺ L - ^—Р ,     (14)

лин где X - коэффициент трения; Lr, Le - соответственно, длина горизонтального и вертикального участков трубопровода, м; О - средняя скорость движения транспортируемой среды в трубопроводе, м/с; р - плотность среды, кг/м3; D - диаметр трубопровода, м.

Потери давления, обусловленные наличием местных сопротивлений, определим по формуле Вейсбаха

А Р .с = Z f -с -р -       <15)

где f -с - коэффициент местного сопротивления.

Гидростатические потери давления определим по формуле

А Р гс =± P gL_e ,           (16)

где g - ускорение свободного падения, м/с².

С учетом формул (14)-(16) имеем

А Р = X ^ - -Р + Z f -с ^ ± '  • . (17)

Уравнение (17) не содержит в явном виде величину объемного расхода Q. Для приведения этого уравнения к виду (12), представим среднюю скорость движения транспортируемой среды в трубопроводе круглого сечения через его диаметр D:

транспортируемой среды Q . Необходимое условие минимизации критерия (1) имеет вид [1, 31]

& —

4Q nD2 .

dF_  d А Р

— S р     + SJ dD PdD

— 0 .

В условиях ламинарного режима течения значение коэффициента трения X зависит от величины числа Рейнольдса Re

Re ,

которое определяется как

Re — & D P, Ц

где ц - коэффициент динамической вязкости транспортируемой среды, Па - с.

С учетом формул (18) – (20) уравнение (17) принимает вид

А Р = ^ [    ' ( L + L b ) ⁺ £ - 1± ^p gL - (21)

^{п D} V P Q             J

Уравнение связи (21) позволяет определить оптимальные значения D и А Р , при которых критерий оптимизации (1) достигает минимального значения при заданном объемном расходе

Решением уравнения (22) является оптимальное значение диаметра трубопровода, которое в дальнейшем используется для определения оптимальных потерь давления по уравнению (21).

Дифференцируя (21) по диаметру D ,

получим

d АР dD

- 32 P Q - С 1 Ц ( L - + l ) + ^ 5 - ] .(23) ^{п D} V P Q             J

Подставляя (23) в (22), приходим к уравнению

_ З^ Г l^ r ( L + L ) +    ¹  +   — 0 .(24)

п ² D ⁵ V p Q г        м^-1   J P

Решая уравнение (24) относительно D и исключая комплексные корни, получим оптимальное значение диаметра трубопровода

0,2

D* — 2 P Q Г 16 ^цп ( l + L ) + У ^ I S P   (25)

2                 г     в          мс

_ ^п V P Q                J S D _

Подстановка решения (25) в уравнение связи (21) позволяет определить оптимальное значение потерь давления в трубопроводе

0,2

АР" — 1 ^ Q r( 16 ЦП ( L - + L , ) + £ §„ )f S D 1    ± p gL . .        (26)

^{2 п} V ^{p Q}                 Jv S p J

Подстановка оптимальных значений А Р * и D * в критерий оптимизации (1) позволяет рассчитать минимальное значение суммарных затрат на сооружение трубопровода заданной трассировки и транспортирование среды с заданными расходом и свойствами.

На рисунке 1 представлена геометрическая интерпретация задачи оптимизации технологического трубопровода. В пространстве ( F ; А Р; D ) представлена плоскость целевой функции (1), уравнение связи (13) для Q = const и кривая, образованная сечением плоскости (1) цилиндрической поверхностью с основанием (13).

Точка A с координатами ( А Р *; D *) является проекцией точки A ( F min ; А Р *; D *) минимального значения критерия оптимизации (в данной точке одновременно выполняются условия (11) и (12), т. е. достигается условный экстремум критерия оптимизации (1).

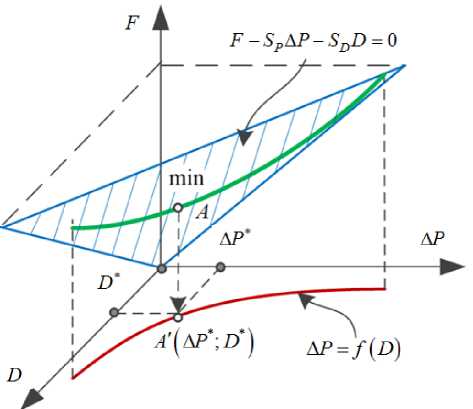
Рисунок 1. Графическая интерпретация задачи оптимизации

Figure 1. Graphical interpretation of the optimization task

Результаты и обсуждение

Обсуждаемую методику оптимизации параметров технологического трубопровода по технико-экономическим показателям проиллюстрируем вычислительными экспериментами на примере гидравлической установки для транспортирования патоки, используемой в кондитерском производстве (рисунок 2).

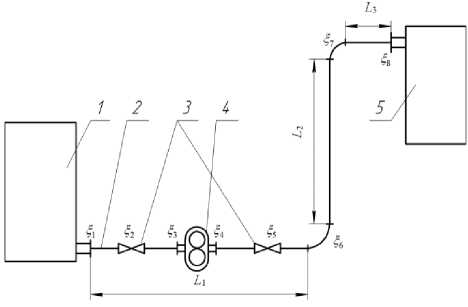
Рисунок 2. Схема установки: 1 – расходная емкость; 2 – трубопровод; 3 – регулировочный вентиль; 4 – насос; 5 – производственная емкость

• Figure 2.    Installation diagram: 1 – consumption capacity; 2 – pipeline; 3 – adjusting valve; 4 – pump; 5 – production capacity

Технологический трубопровод состоит из двух горизонтальных участков длиной, соответственно, L 1 = 20 м и L 3 = 2 м и вертикального участка длиной L 2 = 8 м. Суммарная длина горизонтальных участков L г = 22 м, длина вертикального участка L в = 8 м. Трубопровод содержит местные сопротивления, значения которых представлены в таблице 1.

Для изготовления технологического трубопровода используем трубы электросварные из пищевой нержавеющей стали марки 1 2 x 18Н10Т (зарубежный аналог AISI 304) по ГОСТ 11068–81 «Трубы электросварные из коррозионно-стойкой стали». По прейскурантным ценам методом наименьших квадратов получены значения регрессионного коэффициента a , руб./м², аппроксимирующей функция (3) (таблица 2).

В качестве модельной среды для транспортирования используем патоку с массовой долей редуцирующих веществ 52,7% с температурой t = 40 ° С. При данной температуре плотность и коэффициент динамической вязкости патоки равны, соответственно, р = 1430 кг/м³ и ц = 9,9 Па - с [29].

Вычислительный эксперимент № 1. Заключался в оценке влияния диаметра трубопровода на технико-экономические показатели и определении оптимальных параметров трубопровода для перекачивания патоки с массовым расходом M = 100 кг/ч (объемный расход Q = 1,943 - 10 - 5 м³/с).

Таблица 1.

Значения коэффициентов местных сопротивлений [2]

Table 1.

Values of local resistance coefficients [2]

Местное сопротивление | Local resistance	Значение Value
Вход в трубу | Entrance to a pipe	§ 1 = 0,5
Вентиль | Valve	§ 2 = 4,0
Внезапное расширение | Sudden expansion	§ 3 = 0,64
Внезапное сужение | Sudden constriction	§ 4 = 0,64
Вентиль | Valve	§ 5 = 4,0
Колено (поворот на 90 град.) | Elbow (90 degree rotation)	§ 6 = 1,3
Колено (поворот на 90 град.) | Elbow (90 degree rotation)	§ 7 = 1,3
Выход из трубы | Escaping of a pipe	§ 8 = 1,0

Таблица 2.

Значение регрессионного коэффициента a аппроксимирующей функции (3)

Table 2.

Value of regression coefficient a of approximation function (3)

Диаметр трубы D , мм Pipe diameter D , mm	Толщина стенки трубы 5 , мм Thickness of a wall of the pipe 5 , mm	Коэффициент a , руб./м2 Coefficient a , rubles/m2
6,0 + 20	1,0	8,525 - 10 3
12,0 + 101,6	1,5	10,3 - 10 3
12,0 + 304,0	2,0	13,641 - 10 3
21,3 + 323,9	3,0	18,857 - 10 3
76,1 + 406,4	4,0	28,044 - 10 3

В ходе вычислительного эксперимента значение диаметра трубопровода варьировали в интервале от 0,05 до 0,1 м с последующим вычислением технико-экономических показателей.

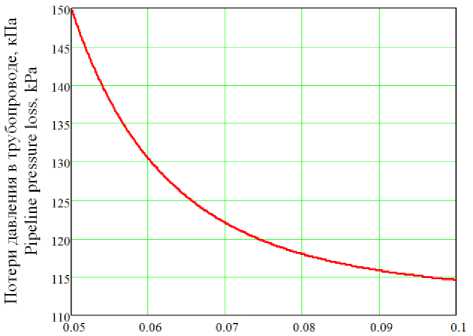
Зависимость потерь давления А Р в трубопроводе от его диаметра D , вычисленная по формуле (21), представлена на рисунке 3.

Диаметр трубопровода, м Pipeline diameter, in

Рисунок 3. Зависимость потерь давления в трубопроводе от его диаметра

• Figure 3.    Dependence of pressure losses in the pipeline on its diameter

Гидравлическая линия проектируется на основе электросварных труб из пищевой нержавеющей стали марки 12 x 18Н10Т, толщина стенки δ = 1,5 мм, значение регрессионного коэффициента a = 10,3 ⋅ 10³ р./м² (таблица 2). Удельные капитальные затраты по формуле (5) составят S D = 3,09 ⋅ 10⁵ р./м.

Коэффициент запаса мощности электродвигателя и КПД привода насоса приняты, соответственно K з = 1,2 и η = 0,8. Продолжительность работы установки в течение суток τ = 8 ч. Тарифная стоимость 1 кВт ⋅ ч электроэнергии (для Воронежской области, декабрь 2019 г.) составляет c эл = 3,74 р./кВт ⋅ ч. Удельные эксплуатационные затраты по формуле (9) равны S P = 0,318 р. / Па.

На рисунке 4 представлены зависимости капитальных, эксплуатационных и суммарных годовых затрат от диаметра трубопровода, рассчитанных, соответственно, по формулам (4), (8) и (10). Как следует из данных рисунка 4, увеличение диаметра трубопровода приводит к возрастанию капитальных затрат (кривая 1) на создание трубопроводной системы для транспортирования патоки при одновременном снижении эксплуатационных затрат (кривая 2) на транспортирование продукта. Экстремальный характер кривой 3 указывает на существование значения диаметра трубопровода, который обеспечивает создание и эксплуатацию гидравлической установки для транспортирования патоки с минимальными суммарными затратами. Вычисления по формулам (17) и (18) дают оптимальные значения диаметра трубопровода D* = 0,063 м и потерь давления ΔP* = 1,27⋅105 Па, при которых суммарные годовые затраты на сооружение и эксплуатацию трубопровода минимальны F* = 5,993⋅104 р./год.

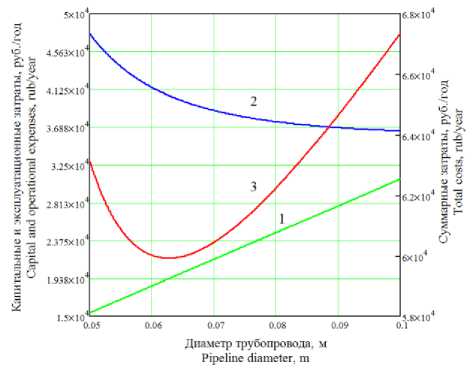
Рисунок 4. Зависимость капитальных (1), эксплуатационных (2) и суммарных годовых затрат (3) на сооружение и эксплуатацию трубопровода в зависимости от его диаметра

Figure 4. Dependence of capital (1), operating (2) and total annual costs (3) for pipeline construction and operation depending on its diameter

Рассчитанное оптимальное значение диаметра трубопровода следует скорректировать по сортаменту труб, согласно ГОСТ 11068–81 «Трубы электросварные из коррозионностойкой стали» с последующим уточнением капитальных, эксплуатационных и суммарных годовых затрат.

Вычислительный эксперимент № 2. Заключался в оценке влияния массового расхода (объемного расхода) перекачиваемой патоки на технико-экономические показатели и оптимальные параметры трубопровода.

Расчет проведен для значений массового расхода M 1 = 100 кг/ч, M 2 = 150 кг/ч и M 3 = 200 кг/ч (объемный расход, соответственно, Q 1 = 1,943 ⋅ 10^–5 м³/с, Q 2 = 2,914 ⋅ 10^–5 м³/с и Q 3 = 3,885 ⋅ 10^–5 м³/с). В ходе вычислительного эксперимента значение диаметра трубопровода варьировали в интервале от 0,05 до 0,1 м с последующим вычислением технико-экономических показателей.

Для электросварной трубы со стенкой толщиной δ = 1,5 мм значение регрессионного коэффициента a = 10,3 ⋅ 10³ р./м² (таблица 2). Удельные капитальные затраты по формуле (5) составят S D = 3,09 ⋅ 10⁵ р./м. Капитальные затраты, в соответствии с формулой (4), не зависят от массового расхода продукта и определяются только диаметром трубопровода (рисунок 4, кривая 1).

Потери давления Δ P в трубопроводе вычислялись по формуле (21). Расчет удельных эксплуатационных затрат выполнен по формуле (9) с исходными данными K з = 1,2 и η = 0,8, τ = 8 ч и c эл = 3,74 р./кВт ⋅ ч. Эксплуатационные затраты рассчитывались по формуле (8). На рисунке 5 показаны зависимости затрат на эксплуатацию трубопровода от его диаметра для заданных значений массовых расходов патоки.

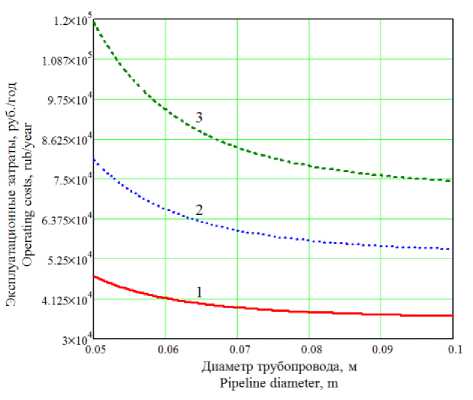
Рисунок 5. Влияние диаметра трубопровода на эксплуатационные затраты при транспортировании патоки в количестве: 1 – 100 кг/ч; 2 – 150 кг/ч; 3 – 200 кг/ч

Figure 5. Influence of the pipeline diameter on the operating costs in the trans-porting of molasses in the amount of: 1 – 100 kg/h; 2 – 150 kg/h; 3 – 200 kg/h

Как следует из данных рисунка 5, увеличение диаметра трубопровода при постоянном массовом расходе продукта приводит к снижению эксплуатационных затрат что связано с уменьшением потерь давления в гидравлической линии. Однако темп снижения затрат на эксплуатацию трубопровода не постоянен и зависит от массового расхода продукта. Так, при массовом расходе патоки M1 = 100 кг/ч увеличение диаметра в 2 раза способствует снижению эксплуатационных затрат примерно на 1,3⋅104 р. год; при массовом расходе M3 = 200 кг/ч аналогичное увеличение диаметра приводит к уменьшению затрат на транспортировку патоки на 4,5⋅104 р. год.

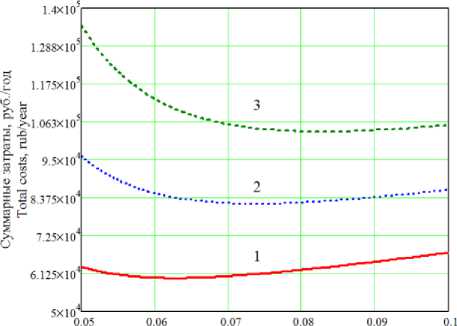
Влияние диаметра трубопровода и массового расхода транспортируемой патоки на суммарные годовые затраты, вычисленные по формуле (10), показано на рисунке 6.

Диаметр трубопровода, м Pipeline diameter, m

Рисунок 6. Влияние диаметра трубопровода на суммарные годовые затраты при транспортировании патоки в количестве: 1 – 100 кг/ч; 2 – 150 кг/ч; 3 – 200 кг/ч

Figure 6. Influence of the pipeline diameter on the operating costs in the trans-porting of molasses in the amount of: 1 – 100 kg/h; 2 – 150 kg/h; 3 – 200 kg/h

Данные рисунка 6 свидетельствуют о существовании значения диаметра трубопровода (при постоянном значении массового расхода), при котором суммарные годовые затраты на создание и эксплуатацию технологического трубопровода достигают своего минимума. Оптимальные значения диаметра трубопровода и потерь давления для заданных массовых расходов патоки вычислены по формулам (17), (18) и представлены в таблица 3.

Таблица 3.

Технико-экономические показатели трубопровода оптимального диаметра

Table 3.

Technical and economic indices of the pipeline of optimal diameter

Массовый расход M , кг/ч | Mass flow M , kg/h	Диаметр D *, м | Diameter D *, m	Потери давления Δ P *, Па | Pressure loss Δ P *, Pa	Капитальные затраты K , р./год | Capital expenditures K , rubles/year	Эксплуатационные затраты Э , р./год | Operational costs Э , rubles/ year	Суммарные затраты F *, р./год | Total costs F *, rubles/year
100	0,063	1,27 ⋅ 105	1,937 ⋅ 104	4,055 ⋅ 104	5,993 ⋅ 104
150	0,073	1,242 ⋅ 105	2,278 ⋅ 104	5,926 ⋅ 104	8,204 ⋅ 104
200	0,083	1,222 ⋅ 105	2,556 ⋅ 104	7,781 ⋅ 104	1,034 ⋅ 105

Эффективность оптимизационных мероприятий ориентировочно оценим по показателю эффективности K эф , %, который можно интерпретировать как "степень крутизны" зависимости F = f ( D, M ) между двумя значениями суммар-

ных затрат: Kэф = F* - Fmax 100 (27) F* где F* – значение суммарных затрат при оптимальном значении диаметра трубопровода D* и заданном значении массового расхода патоки M; Fmах – наибольшее значение суммарных затрат, соответствующее неоптимальному значению диаметра трубопровода при заданном значении массового расхода (таблица 4).

Таблица 4.

Эффективность оптимизационных мероприятий

Table 4.

Effectiveness of optimizing actions

Массовый расход M , кг/ч | Mass flow M, kg/h	Оптимальные параметры Optimal parameters		Неоптимальные параметры Non-optimal parameters		Показатель эффективности K эф ,% | Efficiency indicator K эф ,%
	Диаметр D *, м | Diameter D *, m	Суммарные затраты F *, руб./год | Total costs F *, rubles/year	Диаметр D , м | Diameter D , m	Суммарные затраты F , руб./год | Total costs F , rubles/year
100	0,063	5,993 ⋅ 104	0,1	6,690 ⋅ 104	11,63
150	0,073	8,204 ⋅ 104	0,05	9,515 ⋅ 104	15,98
200	0,083	1,034 ⋅ 105	0,05	1,344 ⋅ 105	29,98

Анализ формулы (27) и результатов вычислительного эксперимента позволяет сделать вывод о целесообразности и эффективности мероприятий, направленных на оптимизацию технологического трубопровода: поиск оптимального проектного решения при данных условиях тем целесообразнее, чем больше значение показателя эффективности K эф и наоборот.

Так, создание установки для транспортирования патоки в количестве 100 кг/ч с оптимальным диаметром трубопровода D * = 0,063 м и ее эксплуатация в течение календарного года при односменном режиме работы обеспечит снижение суммарных годовых затрат на 0,697 ⋅ 10⁴ руб./год. Эффективность оптимизационных мероприятий при этом составит K эф = 11,63%. Создание установки с оптимальным диаметром трубопровода D * = 0,083 м для транспортирования 200 кг/ч патоки и ее эксплуатация при тех же временных режимах позволяет сэкономить 3,1 ⋅ 10⁴ руб./год с эффективностью оптимизационных мероприятий при этом K эф = 29,98%.

Таким образом, экономически целесообразными и эффективными являются проектные решения по созданию высокопроизводительных гидравлических установок, эксплуатирующихся длительное время в течение календарного года. Создание малопроизводительных установок и их непродолжительная эксплуатация возможны без учета оптимальных параметров технологического трубопровода в виду низкой эффективности и экономической целесообразности.

Рассмотренная методика оптимизации технологических трубопроводов по техникоэкономическим показателям, при необходимости, может быть дополнена проверочными расчетами трубопровода и его элементов на прочность, выносливость и вибрацию по соответствующим нормативным документам.

Заключение

• 1.    Предложены расчетные соотношения для определения оптимального диаметра технологического трубопровода из условия минимизации суммарных годовых затрат на его создание и эксплуатацию с учетом текущих цен и тарифов на трубопровод и электроэнергию, трассировки трубопровода, условий его работы, а также свойств транспортируемой среды.

• 2.    Проведены вычислительные эксперименты по оценке влияния диаметра трубопровода на технико-экономические показатели установки для транспортирования патоки с постоянным массовым расходом. Установлено, что увеличение диаметра трубопровода приводит к снижению эксплуатационных затрат на транспортирование патоки при одновременном увеличении капитальных затрат на создание трубопроводной системы. Найдено оптимальное значение диаметра трубопровода, обеспечивающее минимум суммарных годовых затрат на создание и эксплуатацию гидравлической установки для транспортирования патоки.

• 3.    Проведены вычислительные эксперименты по оценке влияния массового расхода перекачиваемой патоки на технико-экономические показатели и оптимальные параметры трубопровода для перекачивания патоки. Установлено, что увеличение массового расхода перекачиваемой патоки приводит к повышению суммарных годовых затрат на создание и эксплуатацию трубопроводной системы. При этом значение

• 4.    Для приближенной оценки эффективности оптимизационных мероприятий предложен критерий, позволяющий сопоставить суммарные годовые затраты на создание и эксплуатацию технологических трубопроводов с оптимальными и отличными от них параметрами.

оптимального диаметра трубопровода возрастает, а потери давления в гидравлической установке незначительно снижаются.