Оптимизация переходной функции модульного источника бесперебойного питания подчиненного типа

Источник бесперебойного питания (ИБП) переменного тока, включающий несколько модулей, соединенных параллельно, позволяет добиться высоких показателей надежности системы путем применения резервирования. Кроме того, ИБП с несколькими модулями обладает свойством масштабирования, то есть построения сборки, соответствующей заданной мощности и ее дополнения (либо уменьшения) в случае необходимости [1; 2].

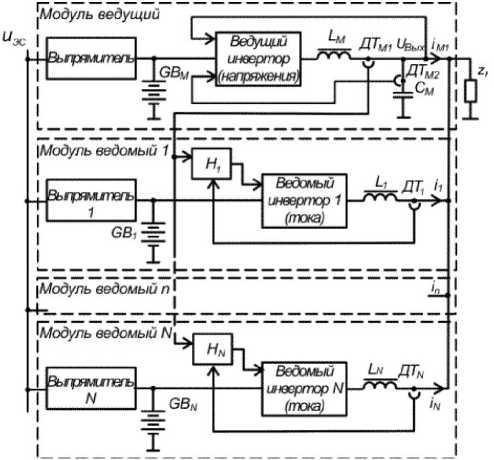
На рис. 1 изображена структурная схема модульного ИБП подчиненного типа, содержащего несколько параллельно включенных модулей, один из которых является ведущим, а остальные ведомыми. Поскольку динамические характеристики ИБП определяются свойствами выходных инверторов модулей, здесь представлены результаты исследований части ИБП, а именно преобразователя с параллельно соединенными инверторами модулей.

Добавим, что на практике часто применяются системы бесперебойного питания, в которых выпрямительное(-ные) устройство(-а), аккумуляторные батареи и инверторы конструктивно и функционально выполняются отдельными блоками.

Математическая модель широтно-импульсного преобразователя представляет собой систему нелинейных дифференциальных уравнений. В нашем случае несущая частота fS широтноимпульсной модуляции значительно превышает модулирующую (fs > [20 ^ 30]fM). Следовательно, применима линеаризация модели на основе метода переменных состояния по усредненным параметрам [3]. При этом методе последовательность импульсов с изменяющимся (относительно медленно) коэффициентом заполнения представляется непрерывной огибающей, ординаты которой соответствуют коэффициенту заполнения.

Линеаризованная модель преобразователя представлена на рис. 2. С помощью ведущего инвертора И_М путем широтно-импульсной модуляции на высокой частоте формируется выходное стабилизированное напряжение квазиси-нусоидальной формы, которое затем фильтруется [1; 3]. Ведущий инвертор – это широтноимпульсный усилитель напряжения задающего сигнала, обеспечивающий качественные характеристики выходного напряжения, форму, стабильность и точность его величины, а также динамические свойства всего преобразователя. В инверторе используется глубокая обратная связь по напряжению и местная обратная связь по току конденсатора С_М .

Ведомые инверторы ( И ₁ – И_N ) являются широтно-импульсными усилителями тока, что позволяет включить их выходы параллельно. В качестве управляющего сигнала ведомых инверторов используется выходной ток ведущего инвертора.

\Модуль ведомый п Г

.Модуль ведущий

%с |

-I- Вырямитепь ■

Ведущий — инвертор |—9 (напряжения)

Ведомый инвертор N (тока)

Ведомый Li nr н инвертор 71—о^-^.....> (тока)

^Модуль ведомый Nj

I Выгрнмтегь

N

\Модуль ведомый 1   ■

Рис. 1. Функциональная схема параллельно соединенных модулей

С учетом главной обратной связи по напряжению передаточная функция замкнутой системы преобразователя имеет вид

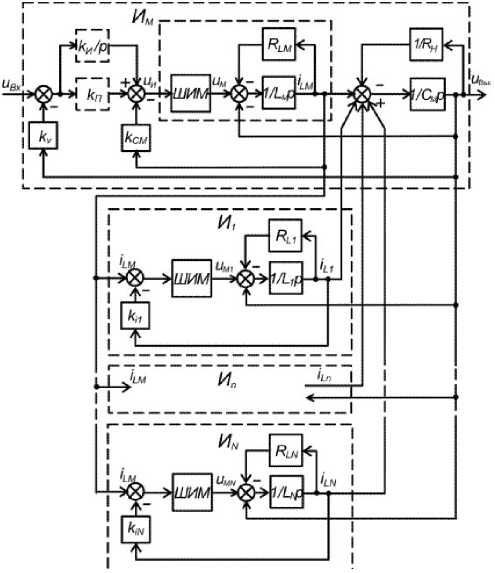
Рис. 2. Структурная схема преобразователя с ведущим и несколькими ведомыми параллельными инверторами

Wn (p) = iN

= wc (р) wMu (p)[1■ A n=iWиn (p) /

i

/Hi + W ic ( p ) W c ( p ) w Mu ( p )

^WiC ^{( p} ) = ^kCM / ) ^CM^{p +}

1          1        V’ N I 1

+        + A

R H ^LM^{p +} R LM     ⁿ = ¹ 1 ^Ln^{p +} R Ln

EN i,,i / \11 n=1WMn (p)jj + iN

+ k v W c ( p ) W Mu ( p ) [ 1 + £ n = 1 W in ( p ) где

W c ( p ) = 1/ ^ c _M p +

N

^^ n = 1

L n P ⁺ R Ln

--1--

R H   L M^{p +} R LM

+

– передаточная функция, образованная конденсатором выходного фильтра и параллельными цепями обратных связей;

^WMu ( P ) = T ^кШ ШМ

^LM^{p +} R LM

– передаточная функция части ведущего инвертора до суммирования токов;

Win (p ) = T7;;nr“h^:^ • Lnp + RLn + кШ nkin n = 1,2,3, _ N

– передаточная функция n -го ведомого инвертора с внутренней цепью обратной связи по току, но без учета выходной емкости;

– передаточная функция цепи обратной связи по току конденсатора после ее переноса на выход преобразователя; k _ШМ – коэффициент передачи широтно-импульсного модулятора ведущего инвертора; k _{Ш n} – коэффициент передачи широтно-импульсного модулятора n -го ведомого инвертора; k _in – коэффициент передачи цепи обратной связи по току n -го ведомого инвертора; L _M – индуктивность дросселя выходного фильтра ведущего инвертора; R _LM – резистивная составляющая сопротивления его дросселя; L _n – индуктивность дросселя выходного фильтра n -го ведомого инвертора; R _Ln – резистивная составляющая сопротивления дросселя.

Анализ передаточной функции W n ( p ) приводит к громоздким выражениям и оказывается весьма трудоемким. Приложение Simulink программного пакета Matlab позволяет в значительной мере автоматизировать вычисления выражения передаточной функции преобразователя и получить в результате кривые выходных процессов линеаризованной модели преобразователя, а также его переходную функцию.

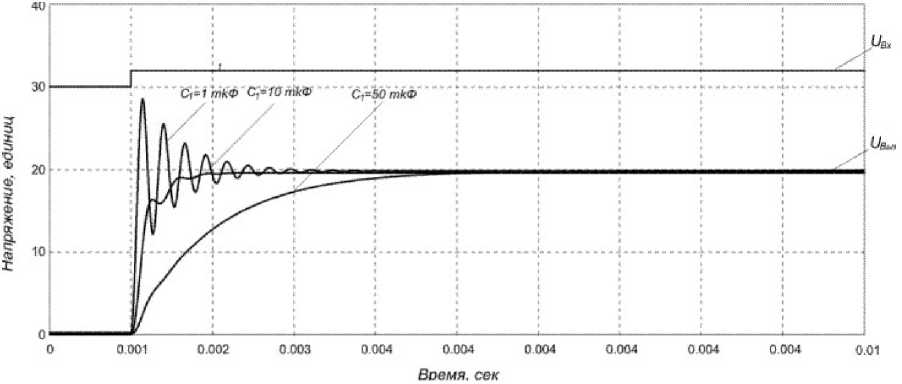
Рис. 3. Переходная функция преобразователя при разных значениях емкости фильтра ( С = 1 мкФ, 10 мкФ, 50 мкФ)

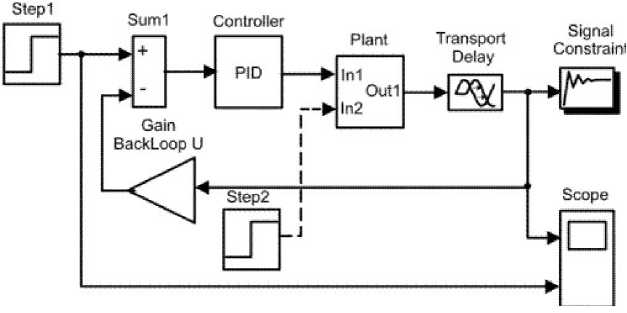
Рис. 4. Структурная схема оптимизация динамических свойств модели преобразователя

На рис. 3 приведены осциллограммы переходной функции преобразователя при различных значениях емкости выходного фильтра и нагрузке R h = 100 Ом. При этом величина коэффициента петлевого усиления напряжения равна k vp ® k vT k v = 200, где k vT = 20000 - коэффициент передачи по напряжению прямого тракта ведущего инвертора, а k v = 0,01 — коэффициент передачи цепи обратной связи по напряжению ведущего инвертора.

Результаты исследования линеаризованной модели преобразователя хорошо согласуются с результатами моделирования импульсной модели, приведенными в работах [2–4]. Однако погрешность результатов исследования линеаризованной модели возрастает в случаях, когда несущая частота широтно-импульсной модуляции снижается.

Как известно, принцип широтно-импульсной модуляции сопровождается неизбежной задержкой или сдвигом фазы выходного широтно-импульсного сигнала модулятора относительно сигнала управления. Более того, в случае цифрового широтно-импульсного модулятора добавляется задержка, обусловленная аналогоцифровым преобразованием и временем обработки сигналов. Во многих случаях эта задержка оказывается пренебрежимо малой, но иногда и ее необходимо учитывать. Таким образом, для повышения адекватности линеаризованной математической модели реальному преобразователю необходимо ввести в модель задержку выходного сигнала преобразователя относительно задающего.

Важнейшим этапом исследований динамических свойств и разработки преобразователя является оптимизация его параметров в соответствии с заданными требованиями. Для оптимизации системы управления преобразователя воспользуемся пакетом Simulink Response Optimization (оптимизация отклика в среде Simulink). С помощью пакета Simulink Response Optimization можно найти оптимальные параметры для линейной (и нелинейной) модели системы, которые обеспечат требуемый переходный процесс по заданным графически ограничениям в окне временной области. На рис. 4 изображена структурная схема модели преобразователя,

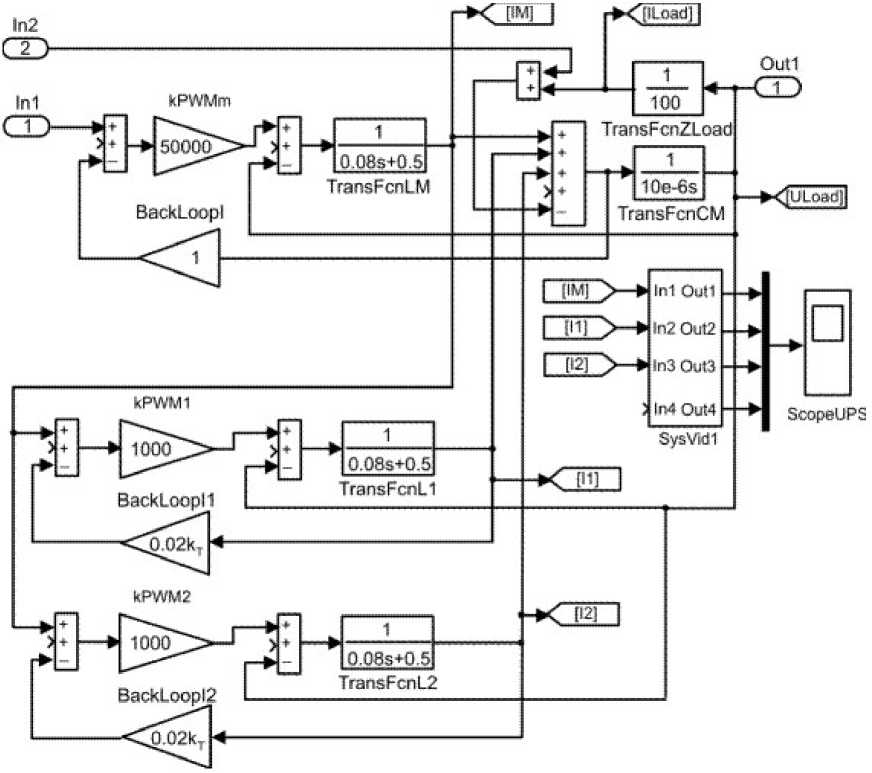
Рис. 5. Структурная схема (разомкнутой) модели преобразователя

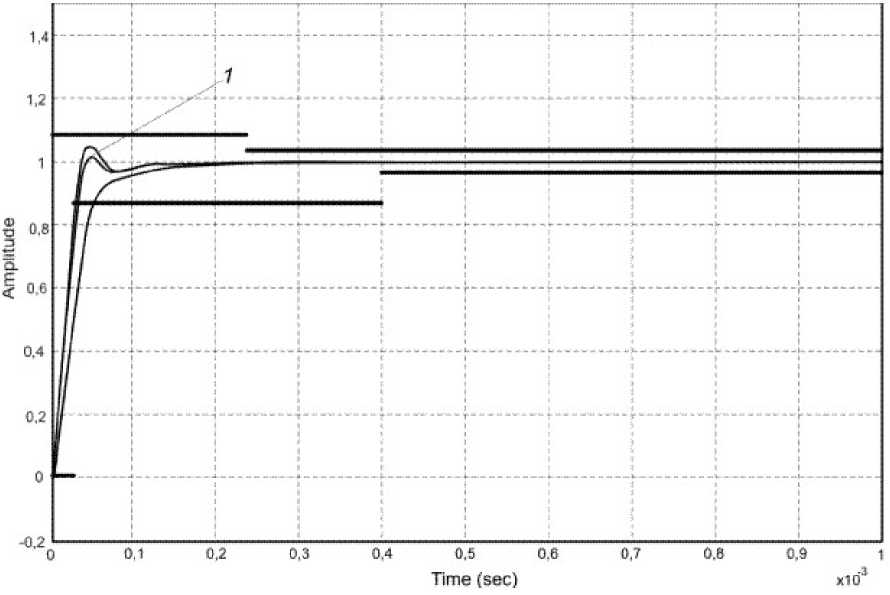
Рис. 6. Результаты оптимизации линеаризованной модели преобразователя с помощью переходной функции

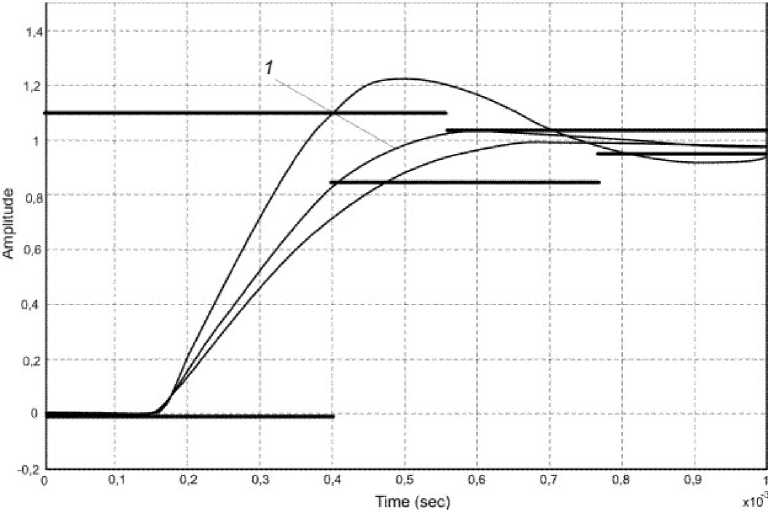
Рис. 7. Результаты оптимизации с учетом фазового сдвига, обусловленного широтно-импульсной модуляцией

в которой с помощью функционального блока Signal Constraint осуществляется оптимизация динамических свойств преобразователя по его переходной функции. Поиск ведется путем итерационной процедуры, которая в общем случае не всегда заканчивается успешно.

На структурной схеме рис. 4 имеется дополнительный блок – PID Controller или пропорционально-интегрально-дифференциальный контроллер с перестраиваемыми коэффициентами k_p , k_i , и k_d . Вместе с этим задающий единичный импульс и импульс возмущения в цепи нагрузки генерируются с помощью блоков «Step1» и «Step2».

Собственно структурная схема линеаризованной математической модели преобразователя на основе ведущего инвертора и двух ведомых инверторов (без цепи главной обратной связи по напряжению) представлена в виде блока «Plant» (рис. 5). Главная обратная связь по напряжению вынесена из блока P l ant и показана на схеме оптимизации в виде цепи с усилителем согласования «Gain BackLoop U».

Еще один параметр, по которому ведется оптимизация, – коэффициент передачи цепи обратной связи ведомых широтно-импульсных усилителей мощности k_T . С помощью этого параметра задается коэффициент передачи усилителя тока. Таким образом, оптимизация динамических свойств преобразователя по переходной функции ведется в пространстве четырех параметров: k_p , k_i , k_d и k_T .

На рис. 6 изображены результаты оптимизации переходной функции линеаризованной модели без задержки фазы. В результате выполнения процедуры оптимизации получены следующие значения коэффициентов для PID-регулятора: k d = 0,3648; k p = 37,0579; k i = 3,3592 при к т = 1. Результирующий переходный процесс оптимизации изображен с помощью кривой 1. Время нарастания (выходного) импульса реакции на входной единичный импульс до уровня 95 % от установившегося значения составляет t_H ® 0,0035 мс.

На рис. 7 показаны результаты оптимизации линеаризованной модели преобразователя с учетом задержки фазы выходного напряжения A t = 0,15 мс, обусловленной широтно-импульсным принципом его преобразования.

Параметры преобразователя в обоих экспериментах заданы для несущей частоты широтноимпульсного преобразования, равной 3 кГц, и нагрузки 100 Ом. Результирующий переходный процесс оптимизации изображен с помощью кривой 1. При этом время нарастания импульса реакции на входной единичный импульс во втором случае составляет t H ® 0, 46 мс.

В результате выполнения процедуры оптимизации получены следующие значения коэффициентов для PID-регулятора: k d = 0,0291; k p = 0,7329; k i = 78,9981 при k_T = 0,9860.