Оптимизация показателей режима резания с переменной скоростью

Аналитически, на базе известных эмпирических моделей получены формулы для определения оптимальной частоты вращения при точении с переменной скоростью резания ( конических, торцовых и ступенчатых поверхностей ) .

Такая обработка довольно распространена и имеет место при подрезании торца и точении конуса или ступенчатой поверхности.

Процесс изнашивания резца при постоянной скорости резания V отражается известной моделью [1]                          h = C • V ^P • t ^X ,                 (1)

где h - накопленный за время t износ по задней грани, C , в и X -эмпирические параметры модели.

В случае торцового точения с постоянной подачей s и глубиной a при постоянной частоте вращения n скорость резания V изменяется согласно следующим моделям (в зависимости от направления подачи):

V = п-d 2-n ^ r. 2-s-n A п • di • n или V =----±-- r 2 • s-n A 1 - t 1 + — t ,     (2) 1000 V d2 > 1000 V d1 > где d 1 = dmin , d2 = dmax, t - время.

За бесконечно малый промежуток времени dt этим изменением можно пренебречь. Тогда для произвольной скорости резания V , дифференцируя модель 1, получим мгновенную скорость изнашивания :

— = X - C • V ^в • t ^ ^-1 . dt

Подставив в эту модель значение t согласно модели 1 и значение V согласно моделям 2, получим (для точения к центру)

hY1 • dh = X-W1 -(1 -B1 • t)PY • dt,                         (4)

где

Y = 1/X,

W1 = CY •

r п* d 2 • n A ^PY

v 1000 ,

2 • s • n d2

Проинтегрировав уравнения 4, получим

hY =-----W[1 - (1 - B. • t)(вY+1)].

B1 • (P-Y +1) L 1 J

Подставив значение t , равное основному времени обработки одной детали, to = (d2 — d 1)/(2 • s • n), получим накопленный за время обработки одной детали износ:

hY =

X-CY d2 (п-d2 P + X " 2-s(1000

1 —

( d (Py+1)

dT

V d 2 V

• n(PY—1) = Kr n(pY—1)

.

Интегрируя уравнения 3 для i -ой обработанной детали, получим

hi - h Y-1) = K1 • n (в 7-1).

Предположим, что после обработки M деталей накопленный износ достигнет предельно допустимого значения h_доп . Тогда, складывая для значений i от 0 до M правые и левые части уравнений 7, получим

hYn = M' K1 • n(р7-1), . (8)

Стойкость резца T = M • t o . Откуда M = T I t o . Подставив это значение M в модель 8, получим

k = KI • n(e1.                                 (9)

^T    h d on

Информация о значениях параметров C и в очень ограничена. Чтобы можно было пользоваться традиционной справочной информацией [2], сравним модели для определения стойкости при постоянной скорости резания.

и

Г с Л ^ц 1

-C H •  .

I а^х • s y ) V ^ц

T = hgn   . 1

( С ) V ^eY

Откуда следует, что

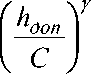
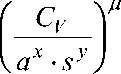
и р-у = ц.

Значения c v , х , у и ц = 1I m есть в справочнике [1].

Критерием оптимизации обычно принимают приведенные затраты ПЗ на изготовление одной детали:

ПЗ = E • [to + (tcu + Зи IE) • (to IT)],                       (11)

где E – затраты на минуту эксплуатации рабочего места; t_си – время на смену затупившегося инструмента; З_и – затраты на эксплуатацию инструмента за период его стойкости. Подставив в модель 11 значения t o и t o I T , получим

ПЗ = E -

d 2 — d 1

2 • s - n

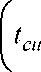
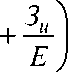
KH • _n ( ц - i) h⁷ h доп

Для определения экономической частоты вращения приравняем нулю производную от ПЗ по n и подставим значения K1 из модели 6. Тогда nэ

1000    CV п-d2• Tm •a*•Sy •

( ^{ц +} 1) •

1 - d1Id2

1 - (d 1I d 2)( Ц+1)

m

где

T3 = (ц -1) • (tcu + Зи IE).

Если определять экономическую частоту вращения nэп , как это принято для максимального диаметра, и не учитывать переменность скорости резания, то

n

эп

1000     CV

----------------------•-------------------------------------------. mxy ^{п d} 2 Т_э • a • s

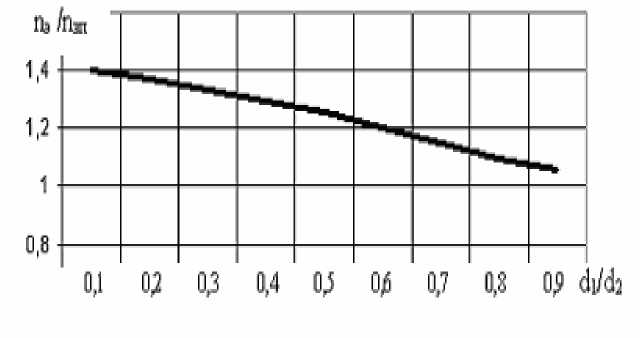
Зависимость отношения п э / п эп от ( d 1 / d 2 ) при m = 0,2 показана на рисунке и может быть аппроксимирована следующей моделью:

пэ / пэп = 1,45 - 0,45 • (d 1/ d2).

Аналитически доказано, что в случае точения торца от центра и конусной поверхности экономическую частоту вращения также можно определять согласно моделям 13 и 14.

В случае точения ступенчатой поверхности при постоянной частоте вращения n с постоянной подачей s и глубиной a скорость резания изменяется ступенчато от V _min до V _max . Тогда при обработке i -й ступени накопленный износ можно определить (в соответствии с выражением 1) из следующей модели:

h i - h 1- 1, = C ^Y • V e’ • t i . (15)

Тогда при обработке одной детали с k ступенями накопленный износ определяется из выражения 16, которое получено последовательным сложением правой и левой частей модели 15 для всех ступеней.

hY = Cy • hod С

^П ) ^{P 7} • n ( P"Y ^{- 1} ) • у ^d i ⁷ • L i

I 1000 J            h s

При обработке за период стойкости N деталей накопленный (допустимый) износ определяется моделью

hYon = N • С •

П )в 7 • n(P-Y-1) . у di 7 • Li11000J            h1   s

,

где N = T / t o . Тогда обозначив

K 3 =

( n )в7 ^dв•• L ( n )ц k^d^ • L

I • i= II • iL

(1000J    t=1    s      (1000J f=1 s ’ где di и Li – диаметр и длина i -й ступени, с учетом модели 10 можем записать

О =

T

( a*

• s

У ^Ц

l Cv

)

• K 3 • n ^{( ц} - 1)

Подставив в модель 15 значение t_o и t_o / T из модели 18, получим

ПЗ = Е •

L ---+ s • n

t_cu + Зи- T — • n ^{( ц} - 1) l си Е ) B ^

< п Лц Ad ^ • L где B = Cv /(a • sy) ,      K3 = 1----- ----L, L - длина

V                  3 l1000J  “1   s обрабатываемой части детали. Приравняв производную от приведенных затрат по n нулю и обозначив dt / dmax = ^t, Li / L = ^t, получим выражение для определения эффективной частоты вращения nэ :

nэ

1000

CV

1

---------------------------•------------------------------------ mxy n d max T э ’ a • s

•

k

m

.

Znf • A l i=1        )

Обозначив n_эп оптимальную частоту вращения, которая определена традиционным методом (по d _max без учета ступенчатости), получим выражение для оценки эффективности по основному времени б % :

5 = 100 •

Пэ

l ^пэп

Л

1 = 100 •

)

km

1/^пГ • A  -1l i=1        )

Расчеты показали , что при обработке ступенчатого вала с указанными в таблице характеристиками

i 1 2 3 4 A 0,1 0,25 0,35 0,3 п 1 0,8 0,75 0,6 выигрыш в производительности по сравнению с традиционным методом оптимизации составляет 29,8%, что довольно существенно.

ВЫВОДЫ

Таким образом , впервые предлагаются математические модели (18 и 26) для определения оптимальной частоты вращения шпинделя в случае точения с переменной скоростью резания на токарно - карусельных и токарно - копировальных станках . Применение этих моделей для массового производства дает довольно ощутимый прирост производительности , зависящий от отношения диаметров элементов детали .