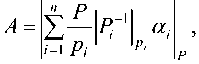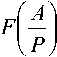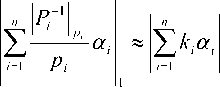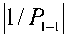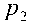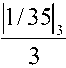Оптимизация процесса коррекции ошибок в системе остаточных классов за счет применения китайской теоремы об остатках с дробными числами

На протяжении всего периода существования вычислительных систем главными целями процесса их развития, в конечном счете, были и остаются повышение их производительности и надежности [1-8]. Основным направлением к достижению этих целей является совершенствование технологии производства средств вычислительной техники и внедрение новых, более эффективных способов организации и проведения вычислений, то есть новых вычислительных структур, например, модулярных процессоров на основе системы остаточных классов (СОК) [2-4]. Анализ известных подходов, используемых при разработке высокопроизводительных и надежных модулярных процессоров, показывает, что все они имеют одну общую отличительную особенность, суть которой состоит в широком применении тех или иных форм параллельной обработки. В этой связи особый интерес представляют исследования по теории и практике разработки модулярных процессоров с параллельной обработкой данных, так как именно такие системы наилучшим образом приспособлены для параллельных вычислений.

Наиболее привлекательными в этом отношении являются вычислительные системы, функционирующие в СОК, обладающие максимальным уровнем внутреннего параллелизма, которые принято называть модулярными процессорами [1-4]. Алгебраическая структура остаточных кодов при введении избыточности позволяет обнаруживать, локализовывать и исправлять ошибки с гибким изменением корректирующих свойств без изменения способов кодирования [4; 9].

Проблема обеспечения эффективности и надежности функционирования вычислительных средств приобретает в настоящее время первостепенное значение, так как техническое обслуживание либо затруднено, либо совсем исключено в силу использования СБИС, имеющих 10 ⁶ и более элементов.

В настоящее время разработку надежных вычислительных модулярных структур реализуют на основе использования СОК [10-14], обладающей высокой степенью однородности, что удачно сочетается со структурами FPGA. СОК активно применяется в цифровой обработке сигналов, системах спутниковой связи, криптографических структурах и др. [15-18]. Использование СОК и FPGA реализует высокую степень однородности, что позволяет существенно улучшить такой параметр, как живучесть [1]. Избыточное кодирование в СОК обеспечивает живучесть архитектуры даже в катастрофических ситуациях, когда поток неисправностей очень велик.

Целью данной работы является исследование, посвященное повышению эффективности определения и коррекции ошибки модулярного процессора. Кроме того, информация, полученная о номере отказавшего модуля, может быть использована для оптимального поиска реконфигурации процессора. Современные алгоритмы, разработанные для контроля ошибок и определения отказов модулярных каналов на основе применения обобщенной позиционной системы счисления (ОПСС), неспособны дать удовлетворительный результат по причине высокой сложности и малого быстродействия [1; 8]. В целях преодоления широко известных недостатков предлагается новый подход к коррекции ошибок на основе Китайской теоремы об остатках (КТО) с дробными числами. Классическая КТО использует целые числа [1; 8].

Введение в избыточную СОК

Сложность современных вычислительных устройств приводит к необходимости применения эффективных средств обнаружения и исправления ошибок, возникающих в результате появления неисправностей оборудования. Ошибки в машинных словах могут быть весьма эффективно обнаружены, если при кодировании этих слов применять метод информационной избыточности. Избыточная модулярная арифметика обладает свойствами, которые можно использовать для обнаружения и коррекции ошибок.

Если фиксированный ряд положительных попарно взаимнопростых чисел Р1,Р^-Р„ назвать основаниями (модулями) СОК, то под системой остаточных классов понимается такая непозиционная система счисления, в которой любое целое положительной число A представляется в виде набора остатков (вычетов) от деления представляемого числа на выбранные основания системы

А = (а1,а2,... ап)

то, в соответствии с КТО [1; 8], представление (1) является единственным, при условии 0где P = P\P.-Pn =Па определяет диапазон представления чисел [o.P-1], то есть существует единственное число 4e[0,P-l], для которого

A = a, (mod Pj),              (3)

где a, – остаток от деления числа A на число Pi и является наименьшим неотрицательным представителем соответствующего класса вычетов по модулю Pi ■ Основным преимуществом такого представления является тот факт, что выполнение операций сложения, вычитания и умножения реализуется достаточно просто, по формуле

A*В = ^ava2,... a„Y^pvp2,... pnV

= ((«[ * Д )mod/?₁,(a₂ * P₂ )mod^>₂,.„     (4)

(«„ *A)mod^J где * обозначает одну из указанных операций: сложение, умножение или вычитание. Эти операции носят название модульных, так как для их выполнения в СОК достаточно одного такта обработки численных значений, причем эта обработка происходит параллельно, и величина числа в каждом разряде не зависит от других разрядов. Рассматриваемые ниже коды СОК могут быть использованы для коррекции ошибок, возникающих при передаче информации или выполнении арифметических операций.

Если в представление (1) добавить разряд ^n-\-\ • равный вычету по дополнительному модулю Pn+V' то получим

Далее будет использоваться обозначение R-Pp.1+i. Если представление (5) удовлетворяет условию где U, – наименьшие неотрицательные вычеты (остатки) числа по модулям Р^Р1’~ Р„- Цифры ai данного представления по выбранным модулям образуются следующим образом

0

то число А однозначно определяется (/7 + 1)-раз-рядным представлением («Р«2>-«,,₊₁). Поэ-

af = А-

Pi

Pi, V7g[l«],

где [d / р, ] – целочисленное частное; Pi – основания (модули) – взаимнопростые числа. В теории чисел доказано, что если ^i^j HO<_P1,p^=\,

тому разряд с основанием Pn+1 можно считать избыточным. Оценим корректирующие возможности кодов СОК с одним и двумя избыточными разрядами по основаниямPn+\ и Pn+2 .

Пусть A = (a_l,a₂,...a„,a_H+1) – переданное сообщение. Для принятого сообщения введем обозначение А (о?,,a₂,... ot_n,(z_n+1). Сообщение

назовем безошибочным, если 0. Если же А>Р,то соответствующее представление назовем ошибочным, так как оно выходит за пределы рабочего диапазона [о.-М- В [1-4] показано, что наличие одного избыточного основания Рп*\ является достаточным для обнаружения всех одиночных ошибок, т.е. если оц = а, при i * ки а_к *а_к (z = 1,2,...,77 + 1), то имеет место неравенство А >Р, которое обнаруживает ошибку.

Необходимо отметить, что введение одного контрольного основания позволяет обнаруживать не только любую одиночную ошибку (в цифре по одному основанию) но и 95% двойных (в цифрах по двум основаниям) [1; 4]. Таким образом, искажение цифры по одному какому-либо основанию превращает это число в неправильное и тем самым позволяет обнаруживать наличие ошибки. Более того, существует только одно-единствен-ное значение этой цифры, которое может превращать неправильное число в правильное. Введение только одного контрольного основания не позволяет в общем случае локализовать ошибочный разряд. Для корректной локализации ошибочного разряда и гарантированного исправления всех одиночных ошибок необходимо введение двух контрольных разрядов Р//-I ’ Ри-1 *

Процесс обнаружения ошибочности полученного представления может быть проведен в процессоре, работающем в СОК. Для этого достаточно перевести полученное представление в ОПСС с теми же основаниями, что и в данной СОК. Если окажется, что старшая цифра ОПСС «,,+1 = 0, то представление безошибочное, если же tz„+i +0, то полученное представление ошибочно. Если известен разряд СОК, в котором имеется ошибка, то ее легко исправить с помощью алгоритмов, изложенных в [1-3].

Описанное выше свойство корректирующих кодов применяется при обнаружении и локализации ошибок на основе метода проекций [1-4]. Проекцией числа А по основанию Pi ’ называется число 4' ’ полученное из А вычеркиванием соответствующего остатка ai и обозначается как Ai=^ava1,...al_val+v...an+rY При i-ой ошибочной цифре полученное число может рассматриваться как число, входящее в альтернативную совокупность чисел, анализ которой позволяет сделать вывод о правильности отдельных цифр. Коррекция ошибок основана на том факте, что при г-2 неразрешенное число оказывается таким, что его проекция Aj может быть разрешенной, где Y = 1,2, ...77 + 1'Y а другие проекции Aj для i*j, U = t2,n + r) являются неразре- шенными. При этом два избыточных модуля позволяют локализовать одну ошибочную остаточную цифру «i . Механизм изоляции ошибочной цифры заключается в нахождении разрешенной проекции A.,. Отсюда следует, что разрешенная проекция A равна по величине числу A и ошибка произошла в i-ой цифре. К тому же правильная величина ai будет правильным числом по модулю Pi, которое позволяет откорректировать i-ую цифру для последующих расчетов по всем модулям СОК.

Таким образом, метод проекций позволяет установить цифру, соответствующую модулю системы, по которому произошла ошибка, то есть обеспечивает ее локализацию. Однако как сам алгоритм определения ошибочной цифры, так и последующая ее коррекция на основе метода ОПСС представляются малоэффективными и затратными с точки зрения практической реализации. Вычисление позиционной характеристики каждой из проекций требует выполнения операции восстановления числа из модулярного представления в ОПСС и последующих вычислений над числами большой разрядности, что вносит значительный вклад как в аппаратные затраты, так и в задержку работы устройства. Возникает необходимость искать другие методы вычисления проекций для реализации механизма обнаружения и коррекции ошибок в СОК. В качестве альтернативы методу определения проекции модулярного числа на основе ОПСС предлагается приближенный метод вычисления проекций, который характеризуется меньшей вычислительной сложностью за счет применения КТО с дробными числами.

Алгоритм коррекции ошибок модулярного процессора на основе использования КТО с дробными числами

В данной работе предлагается использовать приближенный метод на основе КТО с дробными числами для вычисления проекций модулярного числа и коррекции ошибок, который позволяет существенно сократить вычислительную сложность, обусловленную операциями, выполняемыми над позиционными кодами уменьшенной разрядности. Приближенный метод вычисления проекций основан на отношении абсолютных величин анализируемых чисел к полному диапазону, определяемому КТО [1], которая связывает позиционное число А с его представлением в остатках (^-1 >^2 ’•" ^n )’ где ai – наименьшие неотрицательные вычеты числа относительно мо- дулей системы остаточных классов Р\,Р1,- Р„ , следующим выражением

модульная операция (обнаружение ошибки, переполнение и локализация ошибочного разряда), а также исправление ошибочного числа на основе восстановления позиционного числа А по остаткам.

где ^p = t\Pi; р. – модули СОК; II, – муль-1=1

типликативная инверсия Pj относительно Pi Pi =P! P, = PxP2-Pi-xP_l+x-P_n . Если обе части (7) разделить на константу P, соответствующую диапазону чисел, то получим приближение

где k,-^ – константы выбранной системы;

Pi

«i – разряды числа, представленного в СОК, при этом значение каждой суммы будет в интервале [o, 1). Конечный результат суммы определяется после суммирования и отбрасывания целой части

числа с сохранением дробной части суммы. Ве-

личина

/=1

e[O,l) содержит информацию

как о величине числа, так и о его знаке.

Для реализации функции коррекции ошибок модулярного процессора будем использовать избыточную СОК. Предположим, что СОК содержит n рабочих каналов и r контрольных каналов СОК, функционирующих одновременно и параллельно. Тогда алгоритм коррекции ошибок моду-

лярного процессора описывается последовательностью следующих действий.

M,

• 1.    Вычисление констант СОК к = '---c

• 2.    Вычисление приближенных значений ^i^ai и запись их в LUT-таблицы, где ^ – константы найденные в п. 1, 1 < a,< p,■ -1. Адресами выборки значений кд являются разряды СОК a, -, где z = 1,2,... n + r.

3. Вычисление функции FU^ P>

Pi с требуемой точностью, где i = 1,2,... n + r.

приближенного значения

^кд

z=i

в интервале

[0,1)

Конечный результат, выражение (8) определяется

после суммирования дробных чисел и отбрасывания целой части числа с сохранением дробной

части суммы.

4. Конструирование некоторых правил T, ’ У-1;2;3 согласно которым вычисляется j-ая не-

Численный пример алгоритма определения, локализации и коррекции однократной ошибки в модулярном процессоре

Принцип обнаружения переполнения динамического диапазона, определения ошибки, локализации отказавшего модуля и коррекции ошибки покажем на примере. Предположим, что необходимо реализовать функциональный блок для реализации перечисленных функций вычислительной системы, функционирующей в СОК.

Пример. Пусть набор модулей Pi ’ на которых основаны каналы модулярного процессора, равны: A =2, p₂=3, p₃=5, p₄=1. Выберем модули p_x=l, p₂=3 рабочими, а Pi =5, p₄=1 контрольными, тогда полный диапазон будет равен Z^- =2-3-5-7 = 210, а рабочий P = 2-3 = 6.

Пусть правильный результат числа А в СОК равен A = (1,0,3,3), а искаженный A =(1,1,3,3),то есть во втором разряде возникла ошибка: вместо цифры 0 появилась цифра 1, а константа P = 6 по модулям Px.Pi-Pi-Pv равна P = (0,0,1,6). Допустим, что в заданной СОК будут представлены только положительные числа. Для определения переполнения динамического диапазона и ошибки вычислим относительные значения f^p.J и F^IP^ представленные в СОК и сравним их результаты.

Для этого вычислим константы^=k*| ip,-Вычисление F^!Р„_з6^ и F^P/P^ требует суммирования n + г и r дробных чисел, соответственно, для F^IP.^ и f^pip^Y каждое из которых содержит W = [log^-1] бит для гарантированного корректного сравнения [19], где 77 + F – количество модулей СОК, r – число избыточных модулей;

P_ui6=Px -Pl •■••'?„ •Pn+X ■-■P,,₊A P = ^P, -0-

1=1

Для упрощения анализа вычислим константы ^i в виде десятичных дробей, тогда: k_x = 0,5; k₂ ® 0,333, k₃ = 0,6, k₄ = 0,571. Используя ^i •>найдем функции

^F^ / Р_из6 )= 1»!^ + a₂k₂ + a₃k₃ + а_дЦ_А ~

«|1 ■ 0.5 +1 • 0.333 + 3 ■ 0.6 + 3 • 0.571^ ~ 0,346;

F{PI P_m6) = |m^i + m₂F + m₃k₃ + т₄Аг₄|_T » «11-0.6 + 6-0.571^ «0,026;

так как р – кратное модулей Pl И р,„ то т_} = О и т₂ = О. Из результата сравнения 0,346 > 0,026 можно заключить, что H^J>F(P/^J-Этим неравенством установлено наличие ошибки и переполнение динамического диапазона. Для локализации ошибочного модуля найдем относительные значения проекций Aj числа А по каждому из оснований путем зачеркивания цифр а, по основаниям Pi ’ где P_f – диапазон чисел, соответствующий i-ой проекции.

По основанию р_х = 2 выполним действия для системы с основаниями р₂=3, р₃ = 5 , р₄ = 7 получим^pi = Р₂Рз Р₄ = Ю5, тогда р^ =105/3 = 35, ^.,=105/5 = 2*1, P_v_₃ =105/7 = 15.Далее вычислим

- » 0,666; 3

k3 = -	1/+,		1/21
	Рз        5     5

ИЛ=И4

-» 0,142. 7

Тогда

f(_A_v /Р[) = \а₂к₂ + а₃к₃ + а₄к₄^ =

= |1 • 0.666 + 3 • 0.2 + 3 • 0.1421, « 0,692 ;

F(P/ Pl ) = |77?₃£₃ + т₄к₄ 1, =

= 11-0.2 + 6-0.1421, «0,052.

Так как 0,692 > 0,052, то F^Ai/PiY>F(P/P_xY

Аналогичным образом вычислим проекции по основаниям Р₂=^ р₃=5 и р₄=1.

По основанию Р₂ = 3:

р(л2/Р2)= 11-0,5 + 3-0,8 + 3-0,714^ «0,042;

F(P/F) = |1-O,8 + 6-0,714|, «0,084.

Так как 0,042 < 0,084; то р(л/р₂)<р(р/р₂)

По основанию Рз = 5:

F(A₃ /Р₃)«11 ■ 0,5 +1 • 0,666 + 3 • 0,857|, « 0,737 ;

F(P/P3)=|6-0,857|, «0,142.

Так как 0,737 >0,142; то р(л₃/р₃)>р(р/р₃)

По основанию Pa = ^{7 :}

f(v4₄ / P₄)«11 - 0,5 +1 • 0,333 + 3 • 0,2|, « 0,433 ; p(p/P₄) = 11-0,2|, =0.2.

Так как 0,433 > 0,2; то р(л/р₄)>р(р/р₄).

Итак, все результаты сравнений fUj pY и F^P/P^ показывают, что только по основанию P2 =3 относительное значение проекций числа A меньше, чем относительное значение константы P. Следовательно, ошибка произошла в канале по основанию P^ 1 коррекцию ее проведем на основе КТО с дробными числами. В этом случае kx =0,5; k3 =0,8; k4 =0,714. Найдем их двоичные эквиваленты разрядностью F = ll двоичных разрядов как в примере выше, тогда kx = 0,10000000000 ; k3 = 0,11001100110 ;

k₄ =0,10110110110, откуда fYaJpA-h =0,042,_n =0,0000101010 1;

P2 = 7010 = 1000110, тогда

A = F(A₂/P₂\-n P₂ =0,00001010101 x

X1000110 = 0000010,11100111110.

Отбрасывая дробную часть с округлением вверх, получим zl = ll₂=3_l0. Отсюда a₂ = 3mod3 = 0 и восстановленный правильный результат в СОК будет равен Л = (1,0,3,3).

Аппаратная реализация блока коррекции ошибок модулярного процессора

На рисунке 1 приведена архитектура блока коррекции ошибок модулярного процессора. На вход блока поступает исходное число A (tZpCt₂, ... o?_n+r), на выходе формируется откорректированное число A =(«!,6z₂, ... a,_]+rY Входные регистры KG_Pi, где i = 1,2, ... 77 + 1, ... 77 + 7' объемом (« + '')riogP/l бит служат для временного хранения разрядов а, и m_f в СОК, поступающих по входным шинам размером ^/ ^FlogP/l- Схема формирования проекций (СФП- А ) для избыточного диапазона ^изб и схема формирования проекций (СФП- М ) для рабочего диапазона P = M путем реконфигурации формируют кортежи i -ых проекций и единичные сигналы, используемые для локализации ошибочного разряда.

Выходы схем формирования проекций СФП- А и СФП- М поступают на вход LUT/?_; – таблицы суммарным объемом о(/?2⁶ log 77) бит. Для сравнения, процедура преобразования в ОПСС требует o(/7²2⁶) бит при нежестком допущении когда ь,=ь, где bj – количество двоичных разрядов модулей Pi .

Для повышения эффективности алгоритма и удобства анализа его сложности, предпола- гается, что величины модулей имеют одинаковую битовую длину. В LUT-таблицы записываются некоторые округленные дробные числа k«/]2-v и k^/L-v , каждое из которых содержит

N = [log. Pi +1] бит, которые затем суммируются деревом сумматоров

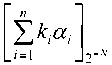
и

/7 + 2

Hkimi j = n + ]

по модулю 1. Точные значения чисел определяются неравенством Ы₂"' <Л-<М₂-л ₊₂-у₊1 .

Результаты суммирования в виде значений

F^/p\ F^MIP^ или F(Ai/P^ и F(.M/Pi)

поступают на схему сравнения (СС), подробное описание которой приведено в [5]. СС формирует сигналы: «ошибка или переполнение диапазона» или «ошибка не установлена».

При определении ошибки выходной сигнал СС поступает на вход «s» триггера ТТ и переводит его в единичное состояние, которое запускает счетчик проекций (СТ). Счетчик проекций управляет реконфигурацией СПФ-А и СПФ-М, которые формируют кортежи i -ых проекций. Кроме того, выходной сигнал СС является стробирующим для схем « И_;», определяющих отказавший модуль СОК.

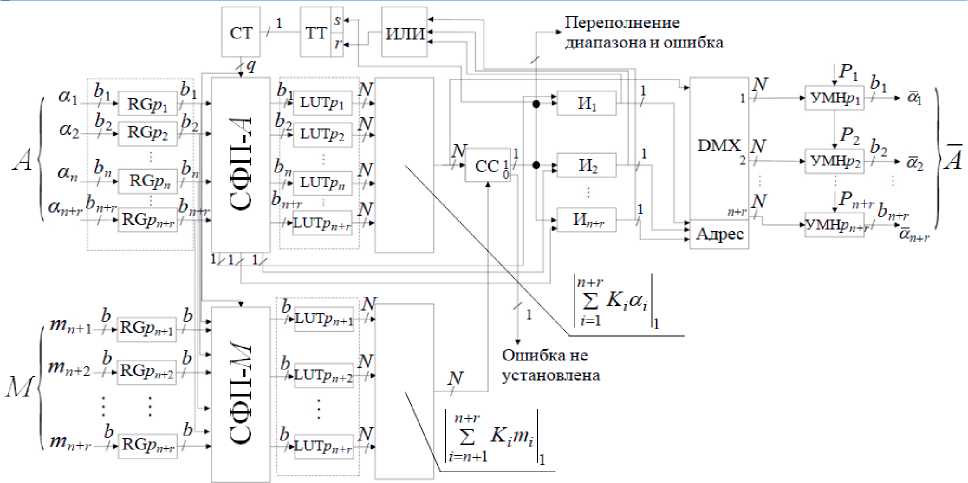
Рисунок 1. Аппаратная реализация блока контроля ошибок модулярного процессора

На вторые входы схем « И_;» поступают сигналы с выхода СПФ- А . Выходные значения схем «И, » используются в качестве адресного кода демультиплексора DMX типа 1: п, где n количество модулей СОК. Информационный вход DMX коммутирует на входы умножителей УМН p_i только проекции 4- так как при анализе числа А адресный код равен(0;0;...0),нулевой выход которого не используется. В исходном состоянии триггер ТТ и счетчик проекций СТ находятся в нулевом состоянии.

Рассмотрим работу блока в режиме определения, локализации и коррекции одиночной ошибки. Контролируемое число Л =(«,,«,, ...а„^ и константа мЦ«н+п«„^- «„+,-) поступают на выходные регистры и далее, соответственно, на входы СПФ-А и СПФ-М. Выходные сигналы схемы формирования проекций числа А (СФП-А) по основаниям р, z = 1,2,... п + г и схемы формирования проекции константы М по избыточным модулям Рп*\’"- Рп+г поступают на адресные входы LUT-таблиц по соответствующим модулям Ps,Pl,- Р„+г и Рп+\’"“ Рп+г LUT-таблиц. В LUT-таблицах записываются округленные дробные числа [^',а,]2-л и [А' /и,]2-л , соответственно, LUTp,, LUTp2, ... LUTp„ и ШТЛ+1, ... ШТЛ,+,.. LUT-таблицы введены для замены операции умножения выборкой ре- зультата умножения.

Выходные значения LUT-таблиц в виде про изведений k«/]2-v и Vkimi ],-л поступают на входы сумматоров

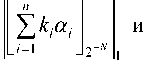
укт

L/ = n + l J2--v J соответственно, где происходит суммирование дробных чисел по modi и формирование значений функций F^AIP^ и F^MIPY Полученные в виде дробных значений результаты суммирования f^a/p) и f(m/p) поступают на входы схем сравнения.

Если

нулевом выходе СС ф

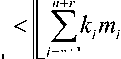
l=n+l

то на rN 1 ормируется «1», которая сигнализирует об отсутствии ошибки и процесс контроля заканчивается, в противном случае, если

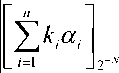
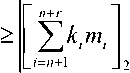
то на пер-

вом выходе СС появляется «1», которая формиру- ет сигнал «переполнение диапазона и ошибка», и поступает на вход «s» триггера ТТ и переводит его в единичное состояние; выходной сигнал триггера запускает счетчик проекций (СТ). Вы- ходные сигналы счетчика поступают на входы схем формирования проекций СФП-А и СФП-М, где формируются кортежи первых проекций чи- сел 4 и М, которые являются адресными входами LUT-таблиц, в элементах которых содержатся произведения \kjttiL и kwJ, , где к. уже новые константы, соответствующие набору модулей

СОК первой проекции.

Выходные значения мируются в сумматорах

LUT-таблиц   сум-

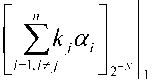
и

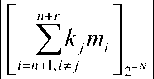
результаты которых поступают на вход СС. Если

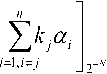
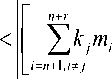
то на первом выходе СС формируется сигнал рав- ный «1», который поступает на все первые входы элементов « И,», где i = 1,2,... n + /•, а на вторые входы элементов « И, » поступает сигнал с выхода блока СФП-А, который соответствует первой проекции, сформированный код на адрес- ном входе DMX коммутирует значение первой проекции на вход схемы умножения УМН p1. Выходной сигнал того элемента « И, », у которого оба входа активные, является индикатором отказавшего модуля и через элемент ИЛИ устанавливает триггер ТТ в нулевое состоя- ние, на этом процесс коррекции заканчивается. Кроме того, выходы элементов « И, » являются адресными входами демультиплексора DMX, который коммутирует i-ую проекцию на вход умножителя по модулю pi (УМН pi), на выходе которого формируется правильное значение ai отказавшего модуля. Так как по условию исправляется только один отказ, то после первого поступившего сигнала на вход «r» триггера ТТ означает окончание контроля и блок контроля переходит в исходное состояние. После анализа первой проекции счетчик проекций CТ формирует следующую проекцию и процесс контроля осуществляется аналогично до определения первого отказа. В худшем случае отказавший канал может быть PnFr .

Моделирование блока контроля

Общая структура алгоритма и блока контроля похожи на известные алгоритмы и схемы, где для формирования проекций используется ОПСС. Предполагается, что СОК содержит n модулей, модулярных процессоров и b бит для каждого из модулей. Предложенный блок контроля использует LUT-таблицы суммарным объемом O^n2^b log z?) бит. Процедура преобразования в ОПСС требует таблицы размером («²2⁶) бит. По сравнению с наиболее эффективными практическими реализациями СОК [20], которые базируются на ОПСС, вычислительная сложность предложенной архитектуры сокращает аппаратурные затраты в n I log n раз на выполнение основной части блока контроля. Элементы оставшейся части блока контроля однотипные, которые используются в известной и предложенной схемах. Сравнение вычислительной сложно сти предлагаемого блока проведем с известным, который реализован на улучшенной архитектуре ОПСС.

Моделирование проводилось с использованием средств среды ISE Design Suite 14.7 на плате Kintex-7 KC705 XC7K70T-2FBG676 без блоков DSP48E1. Данная плата содержит 10250 блоков Slice и 300 блоков ввода/выво-да. Модель выбрана при фиксированном количестве оснований с изменением разрядности модулей. В каждом случае подбирались простые основания системы заданной разрядности, общие для каждого из методов. Было использовано 4 основания с количеством бит модулей 5, 9, 13, 17, 21 и 25. Динамический диапазон системы приближенно равен произведению количества оснований на разрядность каждого из них. На рисунке 2а представлен график, отражающий использование ресурсов платы при использовании модулей различной разрядности для каждого из анализируемых методов.

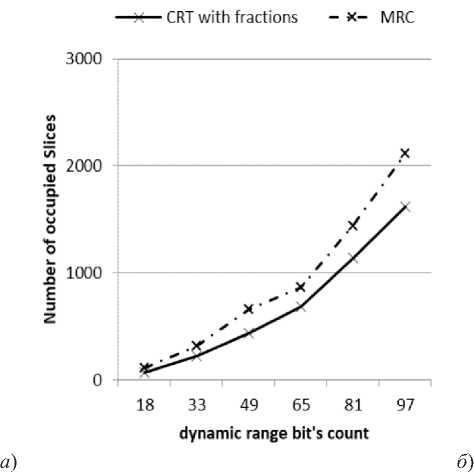
Рисунок 2. Зависимость от разрядности используемых модулей системы:

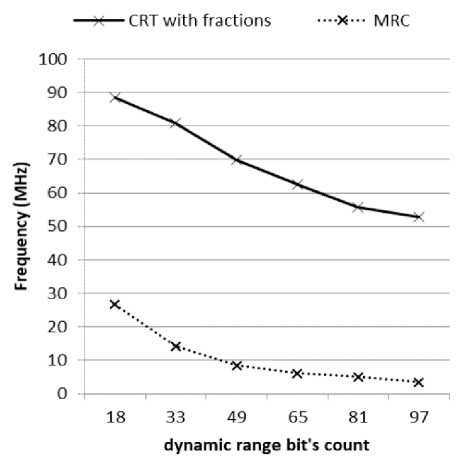
а) от числа использованных блоков Slice платы FPGA Kintex-7 КС705; б) от частоты разработанных схем

Под задержкой схемы будем понимать максимальное время, затрачиваемое на преобразование данных от некоторого входа до некоторого выхода. Оценка задержки позволяет получить представление о быстродействии реализованного алгоритма, в том числе оценить частоту работы схемы. На рисунке 2б представлен график зависимости частоты от разрядностей оснований при моделировании определения, локализации и исправления ошибки с использованием ОПСС и КТО с дробными величинами. В качестве примера рассмотрим разрядность диапазона 64 бит как одну из наиболее распространенных в компьютерных системах. Для того, чтобы можно было представлять числа в данной системе, достаточно представить каждый из четырех модулей 16-или 17-битным числом. Пусть в данном случае система модулей имеет вид {65537, 65539, 65543, 65551}, диапазон данной системы представляет собой 65-битное число, что покрывает диапазон 64 бита. Для данной разрядности приближенный метод на основе КТО с дробными величинами требует всего 689 блоков Slice, в то время как схема ОПСС – 865 блоков. С другой стороны, частота приближенного метода составляет 62,5 МГц, что в 10,1 раз больше, чем улучшенный ОПСС.

Заключение

В этой статье предложены высокоэффективные подходы, которые способны оптимизировать вычислительную сложность предложенного метода проекций модулярного числа при локализации ошибочного разряда с помощью КТО с дробными числами. Благодаря применению КТО с дробными числами в популярном методе проекций нам удалось заменить сложные операторы преобразования чисел из СОК в ОПСС недорогими операциями сложения, что и привело к значительному снижению ресурсов, а также к повышению производительности. На базе платформы FPGA разработаны структуры определения, локализации и исправления ошибок для различных наборов модулей СОК.

Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 18-07-00109 и при поддержке Гранта Президента Российской Федерации МК-6294.2018.9. Авторы выражают благодарность анонимным рецензентам за ценные замечания к рукописи статьи.