Оптимизация процесса прессования семян сафлора в ультразвуковом поле

Сафлор ( Carthamnus ) – род одно-, двух-или многолетних травянистых растений семейства астровых. Средняя урожайность семян составляет 10–12 ц/га, при благоприятных условиях – до 20 ц/га и более. Сафлор выращивают преимущественно как масличную культуру. Его семена содержат 25–37% (в ядре 46–60%) полувысыхающих масла (йодное число: 115–155) и до 12% белка. Сафлоровое масло приближается по вкусовым качествам подсолнечному, ее используют в пищевых целях для изготовления маргарина высокого качества [1, 4].

Для исследования влияния параметров прессования на характер работы пресса и затраты энергии был проведен эксперимент с варьированием всеми факторами. В результате была дана оценка эффектов их взаимодействия. Математическое описание указанного процесса может быть получено эмпирически. При этом математическая модель, имеющая вид уравнения регрессии, найденного статическими методами на основе экспериментов, описывается полиномом второй степени [2].

В качестве основных факторов, влияющих на эффективность процесса, были выбраны: X 1 – частота ультразвука, Гц; X 2 – амплитуда ультразвука, мм; X 3 – давление, создаваемое в зеерной камере пресса, МПа.

Все эти факторы совместимы и некоррелируемы между собой. Изучая их взаимное влияние на процесс, можно подобрать оптимальные режимы прессования.

Выбор интервалов изменения факторов обусловлен технологией процесса прессования и техническими характеристиками пресса.

Критерием оценки влияния выбранных параметров выбран Y – остаточная масличность жмыха, %, при этом частоту ультразвука изменяли от 10 до 50 кГц, амплитуду ультразвука от 30 до 50 мм, давление, создаваемое в зеер-ной камере пресса от 7 до 17 МПа [3].

Для статистической обработки данных исследования применяли центральное ротатабельное униформпланирование, которое позволяло в ходе 20 экспериментов в 3-x кратной повторности получить уравнение регрессии адекватно, описывающее процесс прессования [5].

При обработке результатов эксперимента применяли следующие статические критерии: проверка однородности дисперсий – критерий Кохрена, значимость коэффициентов уравнений регрессии – критерий Фишера.

Для оценки адекватности математической модели был проведен ANOVA (дисперсионный) анализ эксперимента в программе Design Expert v . 10 и получено следующее уравнение регрессии:

Y = 10,67 + 0,91 X_Y + 0,78 X ₂ - 0,43 X - (1) 0,25 XX - 0,57 XX + 0,53 X 2 + 0,87 X 2

Анализ уравнения регрессии (1) позволяет выделить факторы, в наибольшей степени влияющие на рассматриваемый процесс (рисунок 1) .

По данным эксперимента, можно судить о степени адекватности модели, с учетом статистических критериев. В этом случае значение критерия Фишера для b 0 равно 11,48, что говорит об адекватности модели, а p < 0,05 о значимости соответствующих членов уравнения регрессии (1).

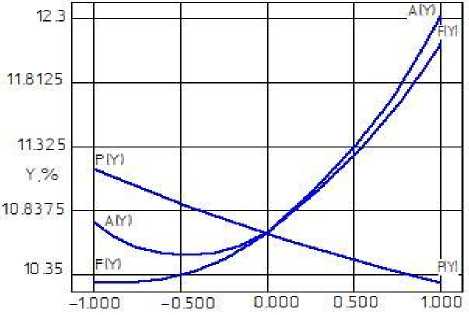
Рисунок 1. Оценка степени влияния коэффициентов b i в уравнении регрессии

Figure 1. Estimation of the degree of influence of the coefficients b i in the regression equation

На рисунке 1 приведена графическая оценка степени влияния числовых коэффициентов b при Х . Функции F(Y) и A(Y) носят возрастающий характер, что подтверждается знаком «+», функция P(Y) – напротив, незначительно убывает. Такое поведение кривых объясняется тем, что при повышении давления в прессе до значения свыше 14 МПа дальнейшее повышение эффективности его работы не наблюдалось при соответствующем увеличении значений частоты и амплитуды ультразвука. Максимальные и наиболее эффективные значения Y получены при значениях частоты в среднем 35–40 кГц, амплитуды свыше 40 мм и давлении в прессе от 10 до 11 МПа. Эти значения, очевидно, зависят напрямую от поведения зерна и движения его внутренней части во время подвода ультразвука [6].

Графическая интерпретация уравнения регрессии представлена кривыми равных значений

и поверхностями отклика для входных параметров в интервале [-1,68…+1,68] (рисунок 2-4).

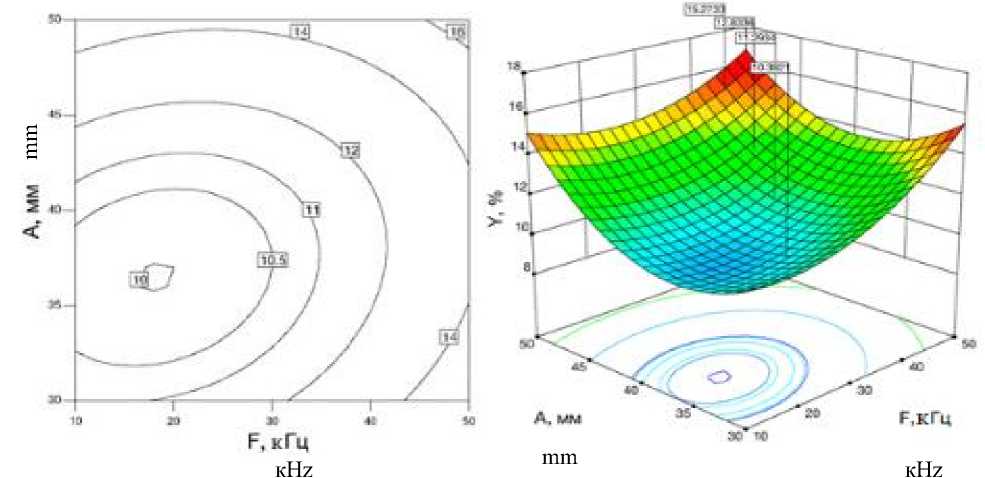
Рисунок 2. Кривые равных значений и поверхности отклика зависимости остаточной масличности, % от частоты ультразвука, кГц и амплитуды ультразвука, мм

Figure 2. Curves of equal values and surface response of residual oil content, % of ultrasound frequency, кHz and ultrasound amplitude, mm

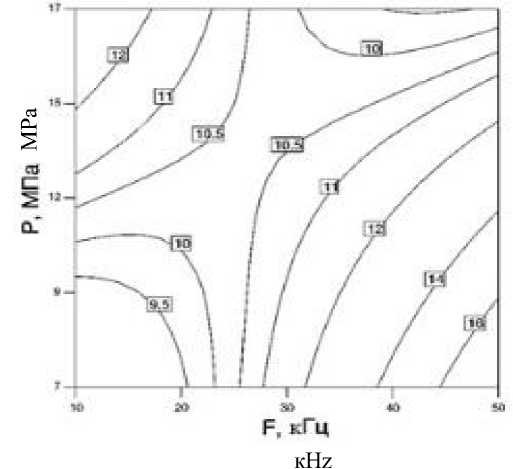
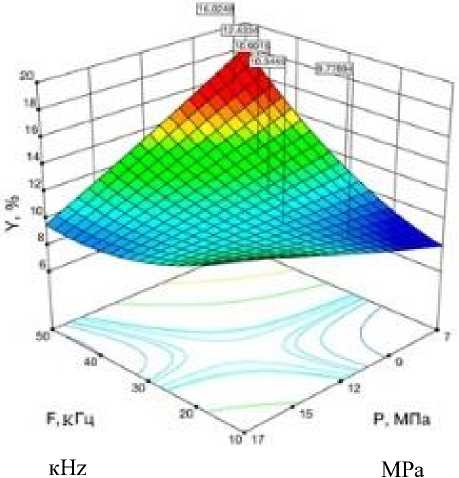
Рисунок 3. Кривые равных значений и поверхности отклика зависимости остаточной масличности, % от частоты ультразвука, кГц и давления в прессе, МПа

Figure 3. Curves of equal values and response surface of the dependence of residual oil content, % on ultrasound frequency, кHz and press pressure, МРа

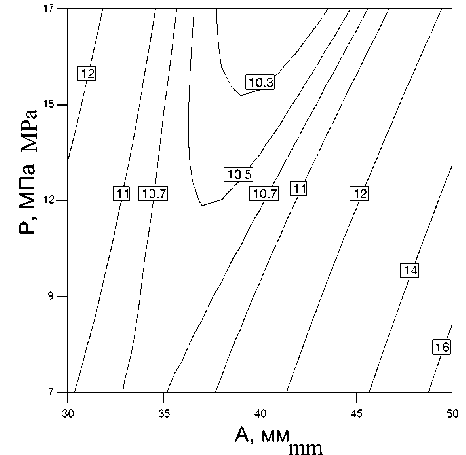
Рисунок 4. Кривые равных значений и поверхности отклика зависимости остаточной масличности, % от амплитуды ультразвука, мм и давления в прессе, МПа

Figure 4. Curves of equal values and the response surface of the dependence of the residual oil content, % on the amplitude of ultrasound, mm and the pressure in the press, МРа

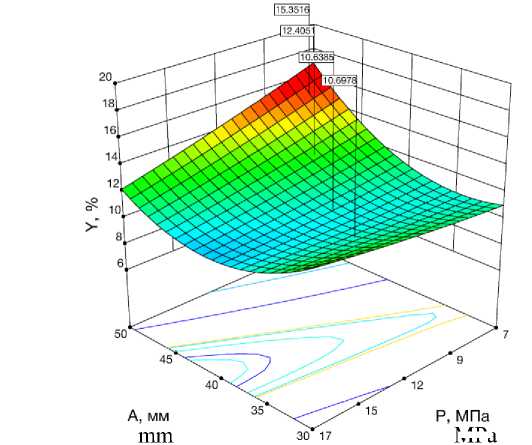
MPa

Проведена численная и графическая процедуры оптимизации для прогнозирования оптимального уровня входных факторов и получения максимального выхода масла по отношению к массе первоначального сырья в %. Общая математическая постановка задачи оптимизации представлена в виде следующей модели:

Y 1 (Х 1 , Х 2 , Х 3 ) → max (2)

Решая задачу оптимизации, определили оптимальные интервалы входных параметров: X 1 = 40,2–41,9 кГц; X 2 = 45,2–45,9 мм; X 3 = 9,1–9,4 МПа.

Графическим методом получена область пересечения оптимального решения (белая область) при заданных критериях (рисунок 5) .

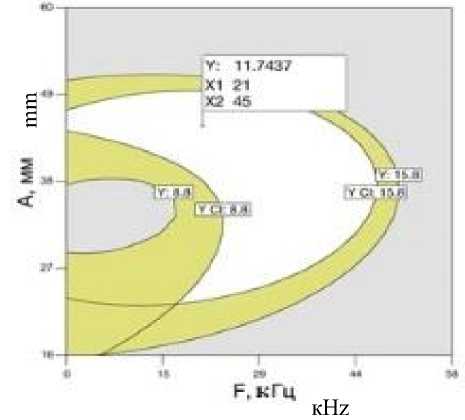
Рисунок 5. Оптимальная область решения задачи оптимизации Figure 5. The optimal area for solving the optimization problem

Заключение

Для проверки был поставлен ряд параллельных экспериментов, полученные результаты попадали в рассчитанные доверительные интервалы по всем критериям качества.

Результаты выполненных исследований могут быть полезны при анализе и расчете параметров процесса прессования.