Оптимизация процесса смешения жидкофазных гетерогенных продуктов на основе многофакторного статистического анализа
Автор: Емельянов А.Б., Копылов М.В., Казарцев Д.А., Абрамян М.К., Нечаев М.В.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Процессы и аппараты пищевых производств
Статья в выпуске: 1 (83), 2020 года.
Бесплатный доступ
Основной задачей экспериментального исследования всех процессов является анализ, изучение и обобщение всех имеющихся результатов. В соответствии с идеей шагового поиска эксперимент проводился в несколько этапов. Число этапов и действия на каждом из них зависели от результатов предыдущего этапа и конечной цели исследований. Конечной целью исследования является определение оптимальных условий протекания процесса перемешивания жидких агрегатоо получения однородной структуры. Исследования процесса перемешивания были проведены на экспериментальной установке, созданной на кафедре. Для обработки экспериментальных исследований был применен программный комплекс STATISTICA 12. Для получения уравнения регрессии матричные данные были обработаны при помощи программного комплекса Microsoft Excel 2010. Для оптимизации процесса, величины выходных параметров преобразованы в безразмерную шкалу желательности d. Установлено, что функция желательности D, характеризующая адекватность полученных значений, имеет экстремум в опыте 12 и составляет 0,733666. Основываясь на полученных данных оптимальными следует считать следующие параметры при перемешивании жидких агрегатов: окружная скорость вала мешалки в пределах 4 м/с, при этом время перемешивания составляет 8 с, а концентрация хладагента 20%.
Моделирование, функция желательности, перемешивание, жидкие агрегаты, хладагент
Короткий адрес: https://sciup.org/140248333
IDR: 140248333 | УДК: 66.011 | DOI: 10.20914/2310-1202-2020-1-47-52
Текст научной статьи Оптимизация процесса смешения жидкофазных гетерогенных продуктов на основе многофакторного статистического анализа
Основной задачей экспериментального исследования всех процессов является анализ, изучение и обобщение всех имеющихся результатов. Полученные данные могут охватывать либо малый диапазон значений, или обширный, на которых строятся первые этапы моделирования. В ходе выполнения поставленной задачи, предварительно составляется весь список имеющихся факторов, из которых необходимо исключить малозначимые факторы, но при этом нельзя пропускать особо значимые
This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License
факторы. На основе вышесказанного завершается предварительная подготовка к экспериментальной части.
Материалы и методы
В соответствии с идеей шагового поиска эксперимент проводился в несколько этапов. Число этапов и действия на каждом из них зависели от результатов предыдущего этапа и конечной цели исследований. Конечной целью исследования является определение оптимальных условий протекания процесса (рисунок 1).
В качестве основных факторов были выбраны: Х1 – окружная скорость вала мешалки, м/с (1–7); Х2 – время смешения, с (2–8); Х3 – концентрация хладагента,% (5–35). Выбранные факторы совместимы и не коррелируемы между собой.
В таблице 1 представлены данные для определения условий опыта. Результаты экспериментальных исследований приведены в таблице 2. Общее число опытов N = 18, число опытов в центре плана N0 = 6, число факторов k = 3, плечо «звёздной» точки r = 1,682.
В качестве функции отклика выбрано Y1 – размер жидких агрегатов, мм (1–6).
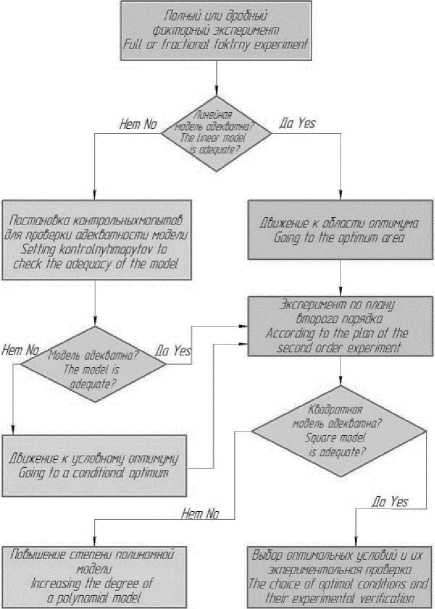
Рисунок 1. Структурная схема экспериментальных исследований с целью оптимизации процесса перемешивания
Figure 1. Block diagram of experimental studies to optimize the mixing process
Таблица 1.
Данные для определения условий опыта
Table 1.
Data for determining the conditions of the experiment
|
Условия планирования Planning Conditions |
Пределы изменения факторов Limits of change of factors |
||
|
Х 1 |
Х 2 |
Х 3 |
|
|
Нулевой уровень (0) Zero Level (0) |
4 |
5 |
20 |
|
Интервал варьирования Range of variation |
2,658 |
3,568 |
17,836 |
|
Верхний уровень (+1) Upper Level (+1) |
4,784 |
6,784 |
28,918 |
|
Нижний уровень (-1) Lower level (-1) |
2,216 |
3,216 |
11,082 |
|
Верхняя «звездная» точка (+1,682) Top “star” point (+1.682) |
7 |
8 |
35 |
|
Нижняя «звездная» точка (-1,682) Lower “star” point (-1.682) |
1 |
2 |
5 |
Экспериментальные исследования проводились на установке, представленной на рисунке 2.

Рисунок 2. Установка для проведения экспериментальных исследований
Figure 2. Installation for experimental research
Для обработки экспериментальных исследований был применен программный комплекс STATISTICA 12.
Для получения уравнения регрессии матричные данные были обработаны при помощи программного комплекса Microsoft Excel 2010.
Уравнение регрессии в физических переменных имеет вид:
Var_1 = -0,322866 – 0,820732 Х 1 + 0,949876 Х 2 +0,425811 Х 3 + 0,0891186 Х 12 – 0,0237339 Х 1 Х 2 +0,00824515 Х 1 Х 3 -0,11633 Х 22 0,0157137 Х 2 Х 3 -0,00754096 Х 32
Таблица 2.
Матрица планирования и результаты экспериментальных исследований процесса перемешивания
Table 2.
Planning matrix and the results of experimental studies of the mixing process
|
№ |
Область факторного пространства The domain of the quotient space |
Выходные параметры Output parameters |
||||||
|
Кодированные Соdеd |
Физические Physical |
Экспериментальные Experimental |
Расчётные Calculated |
|||||
|
Х 1 |
Х 2 |
Х 3 |
Х 1 |
Х 2 |
Х 3 |
Размер жидких агрегатов, мм Size of liquid aggregates, mm |
Размер жидких агрегатов, мм Size of liquid aggregates, mm |
|
|
1 |
-1 |
-1 |
-1 |
2,216 |
3,216 |
11,082 |
3 |
3,414 |
|
2 |
-1 |
-1 |
1 |
2,216 |
3,216 |
28,918 |
4,2 |
5,053 |
|
3 |
-1 |
1 |
-1 |
2,216 |
6,784 |
11,082 |
1,3 |
1,843 |
|
4 |
-1 |
1 |
1 |
2,216 |
6,784 |
28,918 |
2,1 |
2,482 |
|
5 |
1 |
-1 |
-1 |
4,784 |
3,216 |
11,082 |
2,5 |
2,947 |
|
6 |
1 |
-1 |
1 |
4,784 |
3,216 |
28,918 |
4,5 |
4,964 |
|
7 |
1 |
1 |
-1 |
4,784 |
6,784 |
11,082 |
1,4 |
1,159 |
|
8 |
1 |
1 |
1 |
4,784 |
6,784 |
28,918 |
1,8 |
2,176 |
|
9 |
-1,682 |
0 |
0 |
1 |
5 |
20 |
5,7 |
4,761 |
|
10 |
1,682 |
0 |
0 |
7 |
5 |
20 |
4,3 |
4,392 |
|
11 |
0 |
-1,682 |
0 |
4 |
2 |
20 |
5,5 |
4,596 |
|
12 |
0 |
1,682 |
0 |
4 |
8 |
20 |
1,1 |
0,860 |
|
13 |
0 |
0 |
-1,682 |
4 |
5 |
5 |
1,2 |
0,899 |
|
14 |
0 |
0 |
1,682 |
4 |
5 |
35 |
4,1 |
3,257 |
|
15 |
0 |
0 |
0 |
4 |
5 |
20 |
3,8 |
3,775 |
|
16 |
0 |
0 |
0 |
4 |
5 |
20 |
3,8 |
3,775 |
|
17 |
0 |
0 |
0 |
4 |
5 |
20 |
3,8 |
3,775 |
|
18 |
0 |
0 |
0 |
4 |
5 |
20 |
3,8 |
3,775 |
L, мм = 7,8853+0,0188*х-1,3999>0,0784’>Гх+0,0247*Х*у+0,1521*у,У
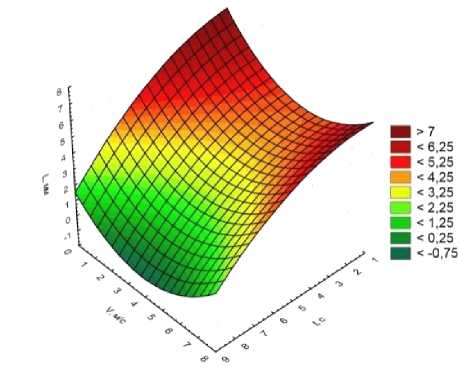
Рисунок 3. Зависимость размера жидких агрегатов от окружной скорости вала мешалки и времени перемешивания
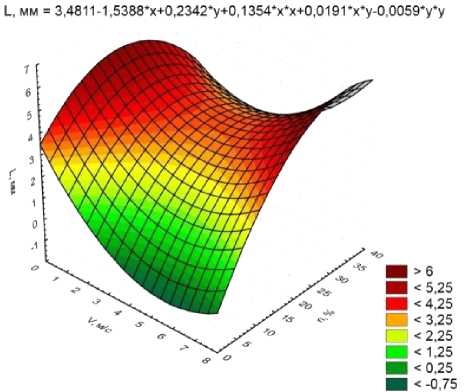
Рисунок 4. Зависимость размера жидких агрегатов от окружной скорости вала мешалки и концентрации хладагента
-
Figure 3. The dependence of the size of liquid aggregates on the peripheral speed of the shaft of the mixer and the mixing time
-
Figure 4. The dependence of the size of liquid aggregates on the peripheral speed of the mixer shaft and the concentration of refrigerant
L, мм = -1,6835+0,4358*x+0,9692*y-0,0081*x*x-0,0086*x*y-0,1472*y*y
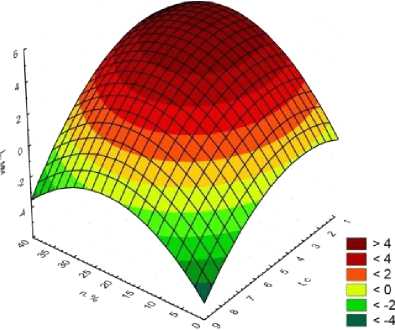
Рисунок 5. Зависимость размера жидких агрегатов от времени перемешивания и концентрации хладагента
-
Figure 5. The dependence of the size of liquid aggregates on the mixing time and the concentration of refrigerant
Результаты и обсуждение
Из рисунков 3–5 видно, что для того чтобы обеспечить требуемый размер жидких агрегатов необходимо установить окружную скорость вала мешалки в пределах 3–5 м/с, при этом время смешения составляет 7–8 с, а концентрация хладагента 17–23%.
Учитывая, что все исследуемые факторы однозначно влияют на величину жидких агрегатов, было проведено исследование по определению оптимальных условий процесса (методом Харрингтона) [8–10].
Для оптимизации процесса величины выходных параметров преобразованы в безразмерную шкалу желательности d (d 1 – выход готового продукта).
Для оценки полученных расчетных данных воспользуемся количественным, универсальным показателем качества – обобщенной функцией желательности D. По максимальному значению, которого можно определить оптимальные параметры процесса.
Согласно формуле:
Y = b о + Z b i X i + Z bM + Z bX (1) где b 0 – свободный член уравнения, который представляет среднюю величину отклика при условии, что исследуемые факторы располагаются на средних, «нулевых» уровнях; i, k – индексы факторов; bi – коэффициенты при линейных членах; bik – коэффициенты двухфакторных взаимодействий, которые показывают изменение степени влияния одного фактора на величину изменения другого; bii – коэффициенты квадратичных эффектов, которые показывают нелинейность выходного параметра от рассматриваемых факторов.
Система уравнений для определения b 0 и b 1 для величины жидких агрегатов примет вид:
1,51 = b0 + 0,86bp
-
- 0,46 = b0 + 5,053bp
где 0,86 – лучшее значение для У 1 (%); 5,053 – худшее значение для У 1 (%).
Отсюда b = - 0,47 и b = 1,91.
В рассматриваемом случае данное уравнение можно ограничить выходными параметрами следующего вида y < Ymax rauY > Y min . Предпочтительной формой преобразования Y в d служит экспоненциальная зависимость:
d = exp[ - exp( - Y ')], (2)
где Y’ = b0 + bjY.
Частные функции имеют следующий вид:
d j = ехр [- ехр ( 0,47 - 1,91 ^ ) ] . (3)
Значения частных функций желательности для всех точек плана, определенные по этим формулам, приведены в таблице 3.
Таблица 3.
Значения частных функций и обобщенной функции желательности каждого опыта
Table 3.
Values of particular functions and the generalized desirability function of each experience
|
№ |
Х 1 |
Х 2 |
Х 3 |
D |
|
1 |
-1 |
-1 |
-1 |
0,997645 |
|
2 |
-1 |
-1 |
1 |
0,999897 |
|
3 |
-1 |
1 |
-1 |
0,953769 |
|
4 |
-1 |
1 |
1 |
0,986137 |
|
5 |
1 |
-1 |
-1 |
0,994264 |
|
6 |
1 |
-1 |
1 |
0,999878 |
|
7 |
1 |
1 |
-1 |
0,839490 |
|
8 |
1 |
1 |
1 |
0,975228 |
|
9 |
-1,682 |
0 |
0 |
0,999820 |
|
10 |
1,682 |
0 |
0 |
0,999636 |
|
11 |
0 |
-1,682 |
0 |
0,999753 |
|
12 |
0 |
1,682 |
0 |
0,733666 |
|
13 |
0 |
0 |
-1,682 |
0,750317 |
|
14 |
0 |
0 |
1,682 |
0,996823 |
|
15 |
0 |
0 |
0 |
0,998818 |
|
16 |
0 |
0 |
0 |
0,998818 |
|
17 |
0 |
0 |
0 |
0,998818 |
|
18 |
0 |
0 |
0 |
0,998818 |
Наглядное представление значений обобщенной функции желательности представлено на рисунке 6.
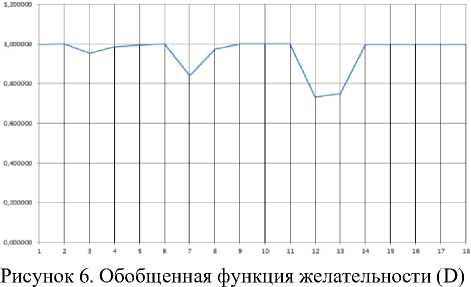
Figure 6. Generalized desirability function (D)
Заключение
В ходе проведенных исследований можно сделать вывод, что функция желательности D, характеризующая адекватность полученных значений имеет экстремум в опыте 12 и равно 0,733666. В основании данного результата оптимальными следует считать параметры: окружная скорость вала мешалки в пределах 4 м/с, при этом время перемешивания составляет 8 с, а концентрация хладагента 20%.
Список литературы Оптимизация процесса смешения жидкофазных гетерогенных продуктов на основе многофакторного статистического анализа
- Копылов М.В., Татаренков Е.А., Ткачев О.А., Горбатова А.В. Оптимизация процесса отжима растительного масла методом математического моделирования // Вестник ВГУИТ. 2017. № 1. С. 28-33.
- Остриков А.Н., Слюсарев М.И., Горбатова А.В., Шендрик Т.А. Диффузионная модель перемешивания сливочно-растительных спредов // Вестник ВГУИТ. 2015. № 3. С. 7-12.
- Rodrigues J. et al. Modeling and optimization of laboratory-scale conditioning of Jatropha curcas L. seeds for oil expression // Industrial Crops and Products. 2016. V. 83. P. 614-619.
- Mateyev Y.Z., Shalginbaev D.B., Mateyeva S.Z., Kopylov M.V. et al. Mathematical modeling of the extracting process of vegetable oil on auger equipment // EurAsian Journal of BioSciences 13. 2019. P. 1875-1880.
- Фролова Л.Н., Василенко В.Н., Копылов М.В., Дерканосова А.А. и др. Оптимизация параметров процесса получения биотоплива методами математического моделирования // Вестник международной академии холода. 2015. № 3. С. 63-67.
- Янчуковская, Е.В. Математическое моделирование химического реактора идеального перемешивания // Известия вузов. Прикладная химия и биотехнология. 2014. № 6 (11). С. 74-80.
- Петров В.Н., Фафурин В.А., Мухаметшина Г.Ф., Малышев С.Л. Математическое моделирование процесса циркуляционного перемешивания двухкомпонентной жидкой фазы // Вестник Технологического университета. 2017. Т. 20. № 15. С. 123-126.
- Shahi S., Ghasemi N., Rahimi S., Yavari H. et al. The Effect of Different Mixing Methods on Working Time, Setting Time, Dimensional Changes and Film Thickness of Mineral Trioxide Aggregate and Calcium-Enriched Mixture // Iranian endodontic journal. 2015. V. 10. № 4. P. 248.
- Basturk F.B., Nekoofar M.H., G?nday M., Dummer P. M. The effect of various mixing and placement techniques on the compressive strength of mineral trioxide aggregate // Journal of endodontics. 2013. V. 39. № 1. P. 111-114.
- Sarli G.O., Filgueira R.R., Gim?nez D. Measurement of soil aggregate density by volume displacement in two non-mixing liquids // Soil Science Society of America Journal. 2001. V. 65. № 5. P. 1400-1403.


