Оптимизация процесса сушки фильтрата послеспиртовой барды

Утилизация послеспиртовой барды является важной задачей, актуальность которой рассмотрена многими исследователями. При этом решаются задачи рационального использования вторичных ресурсов и повышения экологической безопасности производства [1,2].

Одним из таких путей может быть использование фильтрата барды как отдельного продукта в процессе сушки. Для осуществления данного процесса предложено использовать распылительный тип сушки, при этом время сушки составляет 1,5-2 с, а в сочетании с невысокой температурой сушки, порядка 80 С, позволяет получить высококачественный порошкообразный продукт. Такой метод сушки не вызывает денатурацию белков, окисления и потерь витаминов, которыми богат фильтрат барды.

Для исследования взаимодействия различных факторов, влияющих на процесс сушки фильтрата послеспиртовой барды в распылительной сушилке, были применены математические методы планирования эксперимента [1]. Описание данного процесса может быть получено эмпирически. При этом его математическая модель имеет вид уравнения регрессии, найденного статистическими методами на основе экспериментов [2]. Математическая модель изучаемого процесса представляется в виде полинома второй степени: п           п            п

Y = b₀ + ^X + £ b_u-X? + £ b ij -X i -X j i=l           i=l            i

где b0 - свободный член уравнения, равный средней величине отклика при условии, что рассматриваемые факторы находятся на средних, нулевых, уровнях;

X - масштабированные значения факторов, которые определяют функцию отклика и поддаются варьированию;

b ij - коэффициенты двухфакторных взаимодействий, показывающие, насколько изменяется степень влияния одного фактора при изменении величины другого;

Ьц - коэффициенты квадратичных эффектов, определяющие нелинейность выходного параметра от рассматриваемых факторов;

I, j - индексы факторов;

и - число факторов в матрице планирования.

В качестве основных факторов [3] , влияющих на процесс сушки послеспиртовой барды, были выбраны:

X_l - температура сушильного агента, ^оС;

X ? - скорость сушильного агента, м/с;

X3 - скорость вращения диска распыли -тельной сушилки, м/с

X4 - влажность сгущенного фильтрата барды, %.

Все эти факторы совместимы и некоррелируемы между собой. Пределы изменения исследуемых факторов приведены в таблице 1. Выбор интервалов изменения входных факторов обусловлен технологическими условиями процесса сушки послеспиртовой барды в распылительной сушилке и техникоэкономическими показателями процесса.

Таблица 1

Пределы изменения входных параметров

Пределы изменения входных факторов	Кодированное значение	Значение факторов в точках плана
		Х 1 Т в , о С	Х 2 У в , м/с	Х з У д , м/с	Х 4 w , %
Основной уровень	0	70	10	160	65
Интервал планирования	Д	5	1	20	5
Верхний уровень	+1	75	11	180	70
Нижний уровень	-1	65	9	140	60
Верхняя “звездная точка”	+2	80	12	200	75
Нижняя “звездная точка”	-2	60	8	120	55

Критериями оценки влияния входных факторов на процесс сушки послеспиртовой барды были выбраны: Y1 - удельные энергозатраты процесса сушки, к 1 кг испаренной влаги, кВт ч/кг; Y2 - влагонапряжение сушильной камеры, кг/(м-с); Y3 - влажность готового продукта, %.

Выбор критериев оценки Y обусловлен их наибольшей значимостью для процесса сушки послеспиртовой барды. Так, Y₁ определяет энергоемкость процесса и является важным показателем в оц енке его энергетической эффективности, Y₂ определяет производительность процесса сушки и напрямую связан с его скоростью, Y₃ напрямую связан с качеством готового порошкообразного продукта.

Для исследования было применено центральное композиционное ротабельное уни-форм-планирование и был выбран полный факторный эксперимент 24 [1]. При обработке результатов эксп еримента были применены следующие статические критерии: проверка однородности дисперсий - критерий Кохре-на, значимость коэффициентов уравнений регрессии - критерий Стьюдента, адекватность уравнений - критерий Фишера. В результате статистической обработки экспериментальных данных получены уравнения регрессии, адекватно описывающие данный процесс под влиянием исследуемых факторов:

Y₁ = 3,28 + 0,11 • Х₁ + 0,1 • Х₂ + 0,098 • Х₃ + 0,067 • Х₄ + +0,007 •Х₁-Х₂ + 0,005 •Х₁-Х₃ +

+ 0,0112 • Х1 • Х4 + 0,0085 • Х2 - 0,009 • Х2 - 0,0065 • Х32 - 0,014 • Х42

Y2 = 9,94 - 0,23 • Х1 - 0,094 • Х2 - 0,208 • Х3 + 0,204 • Х4 + +0,01 • Х1 • Х2 + 0,105 • Х1 • Х3 -

+ 0,0112 • Х1 • Х4 - 0,0185 • Х2 - 0,0048 • Х22 - 0,0035 • Х32 - 0,002 • Х42

Y3 = 9,13 + 0,39 • Х1 + 0,386 • Х2 + 0,387 • Х3 - 0,25 • Х4 + +0,031 • Х1 • Х2 + 0,032 • Х1 • Х3

-0,011 • Х1 • Х4 - -0,053 • Х2 - 0,071 • Х22 - 0,055 • Х32 - 0,091 • Х42

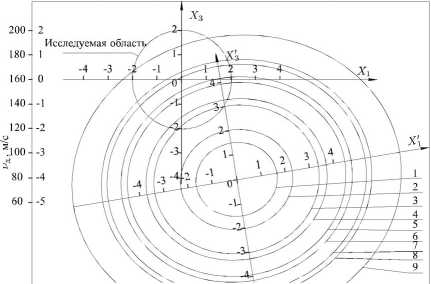
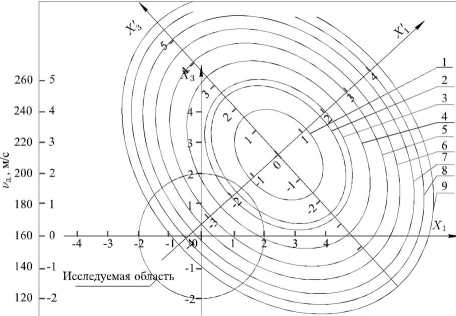
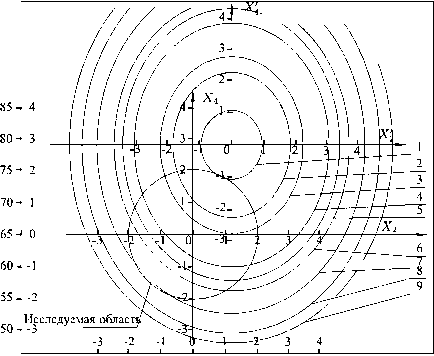
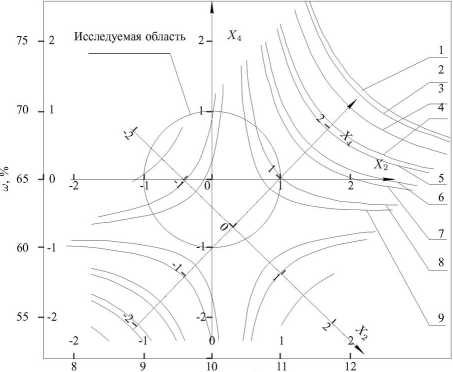
На рисунках 1-4 показаны кривые равных значений выходных параметров, которые представляют научный интерес, позволяют определять значения входных параметров в исследуемой области значений и прогнозировать возможные значения данных параметров вне её.

-4-3-2-101234

321 328 333 338 343 348 353 358 363

Г. К

-4-3-2-101234

321 328 333 338 343 348 353 358 363 Г, К

Рисунок 2 - Кривые равных значений влагонапряже-ния сушильной камеры,, Y_H кг/м ³ ^ч; от температуры сушильного агента, Т, К и скорости вращения диска сушильной установки у д , м/с

Рисунок 1 - Кривые равных значений удельных энергозатрат, Y_H кВтч/кг; от температуры сушильного агента, Т, К и скорости вращения диска сушильной установки у д , м/с

На рисунках 5-6 показаны номограммы для определения значений выходных параметров в исследуемой области значений.

Общая математическая постановка задачи оптимизации представлена в виде следующей модели:

q = q(Y1, Y2,Y3) ^optnpuxED        (5)

Определим область значений:

D:Y1(X1,X2,X3,X4) ^ min

Y2(X1,X2,X3,X4) ^ max        (6)

Y3(Xi,X2,X3,X4)^min

В таблице 2 сведены оптимальные интервалы изменения параметров X t для всех исследуемых выходных факторов.

7    8    9    10   11    12   13   14

Z/C.a., М/С

Рисунок 3 – Кривые равных значений влагонапряже-ния сушильной камеры, Y₂, кг/м3ш; от скорости сушильного агента v_c . _a . , м/с и влажности упаренного фильтрата ш, %

1/с.а., М/С

Рисунок 4 - Кривые равных значений влажности готового продукта, Y₃, %; от скорости сушильного агента v_c . _a . , м/с и влажности упаренногофильтрата ш, %

Согласно критерию оптимизации для принятия окончательного решения по выбору оптимальных режимов исследуемого процесса необходимо решить компромиссную задачу, накладывая оптимальные (таблица 2) интервалы параметров Xt друг на друга.

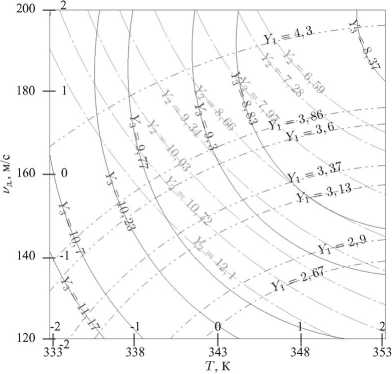
Рисунок 5 – Номограмма для определения значений удельных энергозатрат Y₁, кВтч/кг и влажности готового продукта Y₃, %

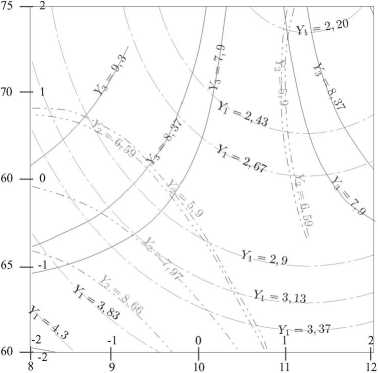
Ус.а., М/С

Рисунок 6 – Номограмма для определения значений энергозатрат Y₁, кВтч/кг ивлажности Y₃, %

Таблица 2

Оптимальные интервалы параметров X t

Y	X 1 , о С		X2 , м/с		X3 , м/с		X4 , %
	min	max	min	max	min	max	min	max
Y i	60	65	8	9	120	140	55	62
Y 2	75	80	11	12	180	200	70	75
Y 3	77	80	10	11	11	200	57	65

В результате были получены рациональные значения интервалов входных факторов:

X1 = 70 - 77 оС;

X2 = 9,5 - 11,5 м/с;

X3 = 160 - 180 м/с;

X4 = 58 - 68 %.

Для проверки правильности полученных результатов был поставлен ряд параллельных экспериментов, полученные результаты попадали в рассчитанные доверительные интервалы по всем критериям качества. При этом среднеквадратичная ошибка не превышала 5,2 %.

Разработанные математические модели сушки фильтрата послеспиртовой барды могут быть использованы при конструкторской разработке технологии распылительной сушки и управляющей аппаратуры для сушилок.

Таким образом, решена задача оптимизации, которая позволила выделить рациональные интервалы изменения входных факторов по трем критериям посредством компромиссных решений.