Оптимизация просветляющих покрытий полупроводниковых оптоэлектронных элементов с учетом спектрального взаимодействия

Рассматриваются вопросы математического моделирования просветляющих покрытий элементов оптоэлектроники с учетом спектрального взаимодействия.

Общепризнанно, что применение оптоэлектроники в вычислительной, контрольно-измерительной технике и системах управления позволяет добиться высоких метрологических характеристик, устойчивости к электромагнитным воздействиям, позволяет создавать помехоустойчивые каналы связи, элементы практически идеальной гальванической развязки измерительных, управляющих и силовых цепей и т.д. В тоже время, оптоэлектронным элементам (ОЭЭ), особенно полупроводниковым, присущ ряд недостатков, сдерживающих их широкое применение. Прежде всего, полупроводниковые ОЭЭ характеризуются низкой температурной стабильностью. Например, величина температурного коэффициента изменения мощности излучения полупроводникового инфракрасного диода доходит до 1,5 %/0С.

С другой стороны, остаются нерешенными некоторые важные моменты теории оптоэлектронного преобразования. Так, под действием внешних дестабилизирующих факторов (ВДФ) и информативнополезных управляющих воздействий изменяются спектральные характеристики ОЭЭ. В результате их изменения возникает эффект спектрального взаимодействия [1]. Игнорирование спектрального взаимодействия элементов при разработке оптоэлектронных устройств приводит к большим погрешностям моделирования. Например, «просветление» поверхности полупроводниковых оптоэлектронных элементов без учета спектрального взаимодействиях приводит к ухудшению их температурных характеристик (рис.1). На рис. 1: ф ( % ,t ), т( % ,t ), Ф_м ( t ) - относительная спектральная характеристика излучения источника излучения (ИИ), пропускания просветляющего покрытия и температурная зависимость максимума излучения ИИ, соответственно.

Рис. 1. Спектральное взаимодействие просветляющего покрытия и излучающего диода

Из анализа характеристик термокомпенсированных по цепи оптического канала ОЭЭ следует,

что для эффективной температурной стабилизации необходимо оптимизировать взаимное расположение спектральных характеристик ОЭЭ и термокомпенсирующего покрытия (ТКП) [2]. В конструктивном отношении целесообразно использование в качестве ТКП тонкопленочных просветляющих покрытий, наносимых непосредственно на поверхность полупроводниковых кристаллов ОЭЭ.

Допустим, что на выводящую излучение поверхность кристалла источника излучения нанесено ТКП, а полоса излучение ИИ достаточна мала, так что его спектральную характеристику можно аппроксимировать функцией Гаусса [3]:

фА( t) = фМ( t ККФ[v-Vф(t)]2, где v (t) = %ф(0 - частота максимума излучения; С - скорость света; t - температура, кФ - параметр аппроксимации. Допустим так же, что поглощение в пленке ТКП отсутствует. Тогда световой поток, прошедший через ТКП с учетом селективности интерференционного покрытия определится [2]:

^v B        /" К ф [ v-V ф ( t )]²

Ф*( t) = Фм (t) TM (t) Г-----:-----------— d v, А ’ MV) mV )] (1 + r 2) + 2 rCos [ Bv ’ vH где T (t) =     16n'n2nз     ; n1, n2, n3 - показатели пре-

^M               2         2

( n + n ₂) ( n 2 + n 3 )

ломления оптической среды, полупроводника и пленки ТКП; _r = ^{( n} з - ⁿ 2^{)( n} 2 - ⁿ 1 ) ; b• = B = ^{4 n n} 2 ^d 2 ;

(n1 + n 2)2( n 2 + n 3)2         C C d2 - толщина пленки; vH,vB - спектральный диапазон излучения ИИ.

Учитывая, что r <<  1 и что для ОЭЭ видимой и инфракрасной области спектра при: v _H >  v >  v _B

£- ^к ф ^{[ v - v} Ф ( t )]²__ _ 0

и,    принимая в первом приближении

V ф ( t ) = V ф o [1 + а , Ф A t ], ^по лу ^чим:

ф А ( t ) =

' п Ф м оГ " ^Ф‘ К ф 1 + r²

Г «          - < 2B 1>!

^х; ! + 2 Z ( - r) ‘ ^f- ^{4 Кф}

Cos [ iB • v ф ( t )]

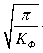
1 - 2 r I

B *²

4 Кф

*

Cos [ B v _{ф 0}(1 + a A t )]

^где    Ф м ( t ) = Ф мo ^ ^-1 " ^A t ,    a = a v Ф - ( « n 2 + « d 2 ); -

a _n2 , « d 2 температурные коэффициенты изменения показателей преломления и толщины пленки ТКП.

Без нарушения общности рассуждений можно принять величину нижней границы изменения температуры равной нулю tн=0, т.к. заменой переменной диапазон изменения t е[t„ и 1 всегда можно свести Н , В к диапазону t е [0, tВ -tН ]. В этом случае величина среднего в диапазоне рабочих температур светового потока определится из выражения:

Ф а о

I ^{п    Ф}м о

K ajt _B (1 + r ²)

в*

2rB e K”    .1

Ч^* - 1 - ^B.₂ [ e " ” [-cos B V „(1 + a _fl ) +

+ sin B V о (1 + a t в )] - (-¹ cos B * V ” о + sin B V о )]) , ^B 2

где b = ^a в V   а погрешность температурной ста-

2 аф Ф билизации определится из выражения:

P M = sup{

” а ( tH )

.Г. *

- 1

” а ( t_B )

.Г. *

” а " ( t N ) Ф А о

- 1},

В

11         1           e4Ks       _ где tN =—{^— [arcsm-== - arcsin—    + 2nN] -1}

« H     71 + В ,      2 rj 1 + В ,

значения

температуры, соответствующие максимумам температурной зависимости погрешности компенсации; N - порядок интерференции.

Оптимальное значение толщины ТКП d_2otr определяется по критерию минимума температурной погрешности в диапазоне рабочих температур, а величина коэффициента преломления п₂ выбирается из условия наилучшего просветления _n 2 = _{П1 n} 3 .

На рис. 2 изображена зависимость максимальной температурной погрешности P_M ^* для арсенидо-галлиевого ИИ при различной толщине пленки d₂ (для двух значений температурного коэффициента некомпенсированного ИИ).

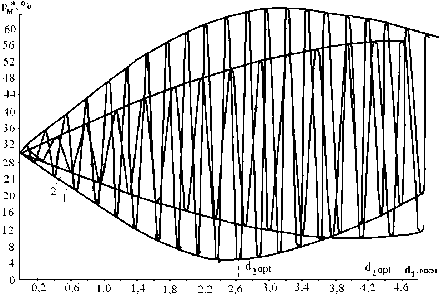
Рис. 2. Оптимизация ТКП

Спектральная характеристика ф п [ 2 - 2 _фмп ( t )] СФЭ определяется из решения линейного интегрального уравнения Фредмгольма первого рода:

λB

Ф м ( t ) • Ф_м „ ( t ) J Ф [ 2 - 2 фм ( t )] • Ф п [ 2 - Л_фМ п ( t )] d2 = Ф А о .

² Н

После преобразований уравнение сводится к виду:

V B

J Ф ( V - U ) Ф п ( V ) dV = f (U ) ,                         ⁽¹⁾

VH где f (U) = ФА о/(ФМ[А2-|(и)Ф„ [A2"I(U)]; V = 2в - 2фмп (t);

А 2 ( t ) = 2 фм ( t ) - 2 фм„ ( t ); U = А 2 ( t ) ; V, = 2 _Н - Л фм. ( t ) .

Получено решение интегрального уравнения (1) в виде:

Ф п [ 2 - 2 м ] = K ” { f f j ( 2 - 2 м ) + п j =)

Ni            N

+ S [⁽-T^L< ^) i ■ !         f i ( 2 - 2 фмп )⁽ j ^{- 2} i ) ]} .

i = 1 i !     4 K ” j = 2 i ⁽ J l )!

Анализ возможных конструктивных вариантов реализации СФЭ, показывает эффективность использования для формирования их спектральных характеристик интерференционных покрытии с переменной по поверхности толщиной пленок и интерференционных фильтров на профилированной подложке. Профиль подложки и закон изменения толщины пленок, также определяются из интегрального уравнения Фредмгольма первого рода.

Разработаны методы компенсации разброса характеристик ОЭЭ в условиях их массового производства. На рис. 3 изображена конструкция полупроводникового излучающего диода с нанесенным на поверхность кристалла ТКП. С части поверхности кристалла ИИ, через которую выводится излучение диода во внешнюю среду, просветляющее термокомпенсирующее покрытие удалено (например, химическим травлением, испарением лазерным или электронным лучом и др.). Изменением соотношения потоков проходящего ТКП и минующего его, изменяется результирующий температурный коэффициент.

Проведенные экспериментальные исследования подтвердили возможность снижения температурной погрешности в Ю-15 раз.

Проведенный анализ температурных характеристик термокомпенсированных ОЭЭ показывает, что применение спектроформирующих элементов (СФЭ) с оптимальной спектральной характеристикой позволяет реализовать устройства с меньшей погрешностью.

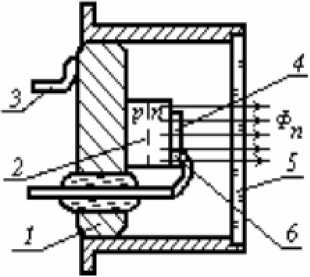
Рис. 3. Подстройка параметров термокомпенсированных ИИ

Представим в первом приближении температурную зависимость интегральной чувствительности приемника излучения термокомпенсированного ” М ( t ) и некомпенсированного Ф_М ( t ) ИИ в виде:

*               *              *

Ф м ⁽ t ) = Ф м 0 (1 + ^a j t ),    Ф м ⁽ t ) = Ф м 0 (1 + ^a j t )

где Ф м 0 = Ф м ( t о ); Ф М 0 = Ф м * ( t о )-

Тогда температурная зависимость интегральной чувствительности Ф ^ приемника излучения для оптрона, с части поверхности излучателя которого удалено термокомпенсирующее покрытие, можно определить из:

Ф, (t) = YnФм*(t) + (1 - Yn)Фм (t), где = qtk - параметр подстройки; Q0, QTK - полная

^Y n    Q 0

площадь поверхности источника излучения и площадь поверхности, покрытая ТКП.

В линейном приближении имеем:

Ф7 (t) - Фм0в7 (1 + a7t), где в7 = 1 + Y. (в -1); а = Ynea1 + (1 Yn)aJ Y      Y„P + (1-Yn)

Откуда имеем: a r =0 при Y n = y ₀

.

где

p _Y = J <  0 параметр перекомпенсации. Таким образом, соотношение поверхностей источника излучения, покрытых и непокрытых ПТП, определяется соотношением температурных коэффициентов изменения чувствительности в режиме перекомпенсации и некомпенсированного МОС. Видно, что величина коэффициента использования ИИ в r возрастает при уменьшении р r , т.е. чем больше перекомпенсация, тем больше коэффициент использования ИИ (рис. 4):

^в ( Y opt ) = ^ В^PY ) ^ 1' P y ^ "” ■

¹ - РР₇

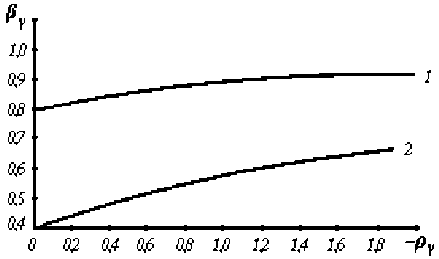
Рис. 4. Влияние параметра перекомпенсации

На рис. 5 (а), (б) изображены экспериментальные температурные зависимости погрешности температурной компенсации изменения мощности излучения арсенидогаллиевого диода при различных значениях параметра подстройки у_n и исходной максимальной погрешности компенсации 8%, а на рис. 6 - зависимость максимальной погрешности температурной компенсации в диапазоне температур 30-130°С в зависимости от величины параметра подстройки y n .

В зависимости (см. рис. 6) наблюдается глубокий минимум при y _n .= Y opt =0,33. Здесь максимальная погрешность компенсации снижается более чем в 10 раз. Расхождение результатов расчета и экспериментальных данных не превышает 15%.

а)

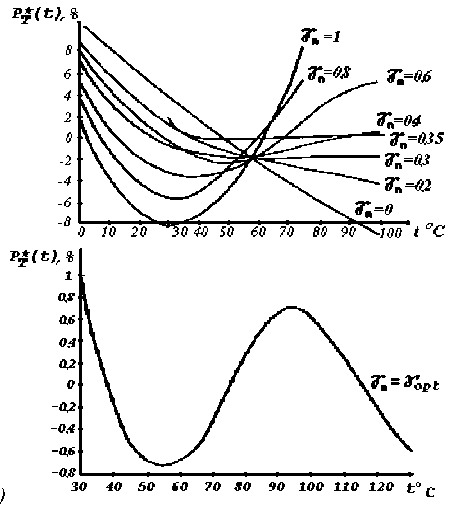
Рис. 5. Зависимость погрешности термокомпенсации от параметра подстройки

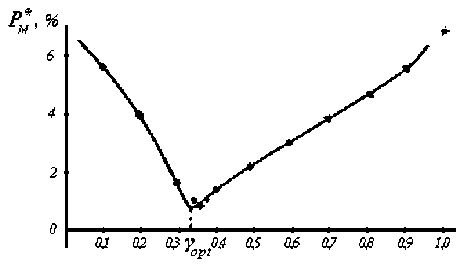
Рис. 6. Погрешность термокомпенсации (* - экспериментальные значения)