Оптимизация распределения отдельных возрастных групп молодежи по направлениям подготовки в условиях неопределенности

Структурные преобразования, происходящие в Крымском регионе в современных условиях, актуализировали вопрос эффективного обеспечения основных направлений развития территории квалифицированными специалистами и рабочими кадрами за счет представителей молодежи по причине явного несоответствия системы высшего и среднего профессионального образования основным потребностям рынка труда. Проблема проявляется в избыточном выпуске специалистов и квалифицированных рабочих в отдельных видах экономической деятельности, в то время как приоритетные сферы (промышленность, строительство, сельское хозяйство и др.) испытывают острый дефицит в молодых специалистах с высшим образованием и квалифицированных рабочих кадрах, имеющих среднее профессиональное образование.

Представленная работа продолжает исследование, начатое в статье «Моделирование кадровых потребностей реального сектора экономики Республики Крым» [1, с. 45–48]. Его актуальность обусловлена в первую очередь тем, что задача оптимального набора абитуриентов в возрасте 15–17 лет на первый курс образовательных организаций, обеспечивающих подготовку специалистов со средним профессиональным образованием (СПО) и высшим образованием (ВО), содержит несколько факторов неопределенности. В этих условиях использование нечеткомножественного подхода (НМП) для оптимизации набора в учебные учреждения, по нашему мнению, в наибольшей степени соответствует реальной ситуации.

Целью исследования является разработка математической модели для оптимального распределения абитуриентов по направлениям подготовки и специальностям с использованием НМП. Рассмотренная задача решена на примере данных Республики Крым. При подготовке математической модели применяли следующие рабочие гипотезы:

• 1)    В регионе имеет место дефицит рабочей силы, т. е. потребность работодателей в работниках, заявленная в территориальных отделениях Центра занятости населения, превышает количество зарегистрированных безработных.

• 2)    Наблюдается незначительный уровень переквалификации рабочей силы.

• 3)    Основной источник пополнения региональной рабочей силы – местное население в лице выпускников средних профессиональных и высших образовательных организаций.

• 4)    Почти все выпускники общеобразовательных учреждений продолжат обучение.

• 5)    Практически все выпускники СПО и ВО будут работать по специальности.

В таблице 1 сведены оценки потребностей крымских работодателей в специалистах со СПО через два года и специалистов с ВО через четыре года, а также данные о наличии бюджетных мест для приема абитуриентов на первый курс учреждений среднего профессионального и высшего образования.

Таблица 1 - Данные о потребности регионального рынка труда в рабочей силе и наличии бюджетных мест в организациях ВО и СПО

№ п/п	о ° X ф 11 о л х q О Ф - ф 54 X CD	3 н ф н X о. о X о. с	го* ф S ° 3 со 5 ф * ч 2 ю	5 -^ о ® О X ° S ji го о.	го* ф S о ф с 3 ° н ф * Ч 2	н $ о ® Z ® ю 5 ф ф it О io с го О а-	2 О л с н ° Ф X §о 2 со (О о 2н ф о О Ф CD S	о >х О ф 5 5 Ф н го и ” го О
1	Сельское   хозяйство, рыбное хозяйство	8	780	500	996	2 500	1 776	3 000
2	Промышленность	10	450	600	2 435	3 100	2 885	3 700
3	Строительство	9	495	1 450	270	5 050	765	6 500
4	Деятельность отелей, ресторанов, санаторнокурортных организаций	6	515	550	284	2 200	799	2 750
5	Финансовая деятельность	3	540	500	514	1 000	1 054	1 500
6	Государственное управление	2	90	450	0	0	90	450
7	Образование	4	1 117	600	130	815	1 247	1 415
8	Здравоохранение и социальная помощь	7	710	700	325	2 600	1 035	3 300
9	Информационные технологии	5	390	850	265	1 650	655	2 500
10	Другие виды экономической деятельности	1	3 293	950	1 761	2 050	5 054	3 000
Итого			8 380	7 150	6 980	20 965	15 360	28 115

* Составлено авторами на основании данных официальных сайтов образовательных организаций высшего и среднего профессионального образования.

** Информация предоставлена ГКУ РК «Центр занятости населения» на основании опроса крымских работодателей всех форм собственности.

Рабочие гипотезы выполняются практически по всем видам экономической деятельности. При этом имеются следующие виды информационной неопределенности:

• 1)    Неизвестна точная потребность в рабочей силе по главным видам экономической деятельности: данные таблицы 1 приведены, в частности, на основании экспертных оценок.

• 2)    Неизвестно реальное количество абитуриентов по базовым направлениям подготовки.

Из этого следует, что оптимизация распределения выпускников по направлениям подготовки выполняется в условиях информационной неопределенности. Поэтому целесообразно разработать математическую модель с использованием НМП, которая позволит оценить оптимальный набор абитуриентов по направлениям обучения с учетом потребности в рабочей силе реального сектора экономики и бюджетных средств, выделенных на их подготовку.

Учитывая наличие информационной неопределенности в исходных данных, воспользуемся НМП для оптимизации распределения абитуриентов по направлениям подготовки. Нечеткомножественный подход к решению оптимизационных задач предложен учеными Р. Беллманом и Л. Заде [2]. Его суть состоит в том, что целевую функцию (ЦФ) и элементы системы ограничений математической модели заменяют функциями принадлежности (ФП) указанных элементов задачи к области допустимых (желаемых) для лица, принимающего решения (ЛПР), значений. В качестве решения задачи оптимизации выбирают такой набор искомых переменных, при котором минимальное из всех значений ФП достигает максимума.

С использованием НМП задача математического программирования (ЗМП) сводится к исследованию на максимум пересечения множества ФП:

X о = argmax min [ W i ц( X), w 2 ц( X) ,..., w , щ( X )] ,

где U - область допустимых решений (ОДР) задачи;

min [ W i ц( X), w 2 Ц>( X) ,..., W , Ц( X )] - пересечение всех взвешенных ФП задачи;

X d

W n - весовые коэффициенты элементов задачи, нормированные на единицу:

n =N

УWn =1, n =1

N - количество элементов ЗМП (целевых функций и ограничений).

Весовые коэффициенты, входящие в формулу (1), позволяют ранжировать направления подготовки по предпочтению ЛПР или степени дефицитности квалифицированных специалистов и рабочих кадров. На практике для элементов ЗМП обычно используют ФП, представленные на рисунке 1.

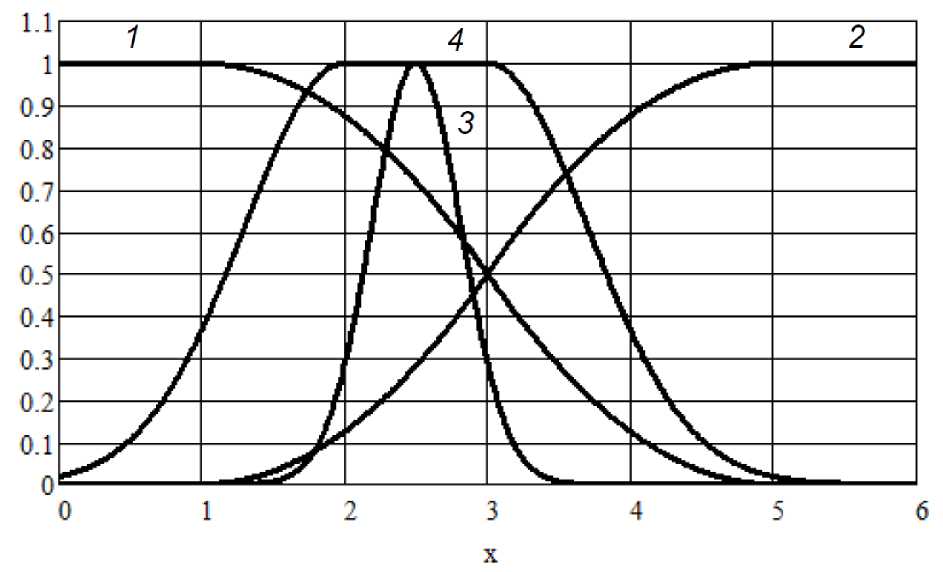
Рисунок 1 – Функции принадлежности: 1, 2 – S-образные, 3 – П-образная, 4 – LR-типа

Функцию 1 (см. рисунок 1) используют для элементов ЗМП, которые должны быть меньше заданного уровня (на рисунке 1 меньше единицы); 2 - для элементов ЗМП, которые должны быть больше заданного уровня; 3 - для элементов, которые должны принимать заданное значение;

4 - для элементов, ограниченных двусторонним неравенством. Известно несколько аналитических выражений для ФП [3]. Отметим, что на практике часто применяют и кусочно-линейные аппроксимации ФП, показанные на рисунке 1, так как они проще вычисляются на ЭВМ.

Получим ФП элементов рассматриваемой задачи для квалифицированных специалистов с ВО. Прежде всего отметим, что данная задача помимо информационной неопределенности обладает и целевой неопределенностью, так как в зависимости от конъюнктуры рынка труда может изменяться цель оптимизации распределения абитуриентов по направлениям подготовки. Например, в случае нехватки абитуриентов необходимо обеспечить максимальный их набор на бюджетные места по наиболее дефицитным направлениям подготовки; при превышении количества выпускников общеобразовательных организаций аналогичная задача стоит для приема на контрактные места в рамках лицензии и т. п. В качестве ЦФ при этом можно взять желаемое общее число абитуриентов. При этом ФП будет иметь пикообразную форму (рисунок 2, кривая 1).

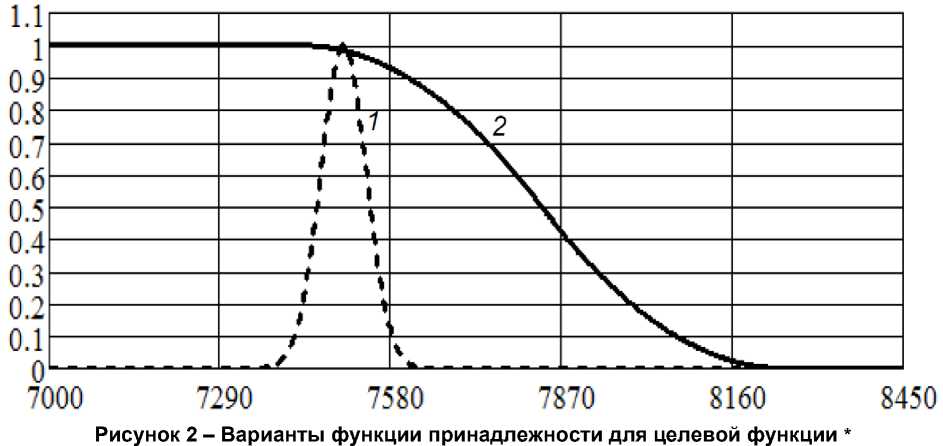
* Пояснения см. в тексте.

Отметим, что желаемое количество абитуриентов может выступать и как ограничение при решении данной задачи, тогда ФП будет иметь S-образную форму (рисунок 2, кривая 2). В данном случае желаемое общее число абитуриентов образовательных организаций приблизительно равно 7 500. При решении задачи использована S-образная ФП, показанная на рисунке 2.

Так как ограничения по количеству абитуриентов описываются двусторонними неравенствами, то для них следует использовать ФП LR-типа, показанную на рисунке 1 под номером 4. Математическое выражение для ФП LR-типа имеет следующий вид:

• 1 ,    ес a Irx < b ,

  д x( p , A , a , b , B ) = *

  
  

  exp [ - ( a -x )/( A -a )|^P ], ес x

  
  
  
  

exp [ - ( x —b )/( B -b )|^P ], ес a A>, где p - параметр для регулировки скорости возрастания и падения кривой 4 (см. рисунок 1);

• A , B - координаты левой и правой точек перегиба кривой;

• a , b - координаты начала и конца отрезка, на котором элемент ЗМП принимает желаемое значение (должно выполняться неравенство A < а < b ).

С помощью данных таблицы 1 для каждого направления подготовки легко получить ФП для необходимого количества абитуриентов с учетом потребностей работодателей и общего числа бюджетных мест в образовательных организациях:

Ц1( х ) - ц х ,2,300,450,550,650), |13( х ) - ц х (2,400,450,550,600), |15( х ) - ц х ,2,400,450,550,600), Ц7( х ) - ц х ,2,500,550,650,700),

р12( х ) - ц х (2,400,430,490,550), Ц4( х ) - ц х (2,450,490,550, 600), Ц6( х ) = ц х (2,40,70,110,120), Ц8( х ) = ц х {2,600,650,750,800),

Ц9( х ) - ц х ,2,300,350,420,450),

|110( х ) - ц х {2,850,900,1 000,1 050) .   ₍₄₎

На рисунке 3 показаны ФП для ограничений задачи с параметрами, указанными в формуле (4).

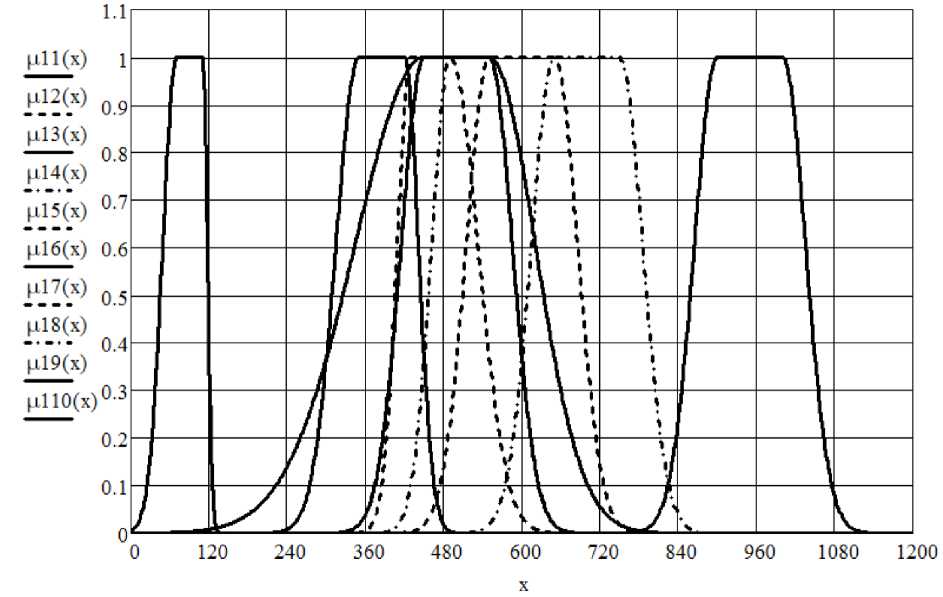
Рисунок 3 – Функции принадлежности системы ограничений

Весовые коэффициенты направлений подготовки представлены в третьем столбце таблицы 1. Коэффициент для ЦФ возьмем равным единице. После нормировки получим следующие значения весовых коэффициентов ФП, входящих в формулу (1): w = {0,143 0,179 0,161 0,107 0,054 0,036 0,071 0,125 0,089 0,018 0,018}.

На основании данных анализируемой таблицы 1 область поиска неизвестных можно описать следующими предельными значениями:

X min = {450 420 450 470 450 70 550 650 350 900};

X max = {550 500 550 550 550 110 650 750 400 1 000}.

В данном случае X max выбиралось меньшим среди значений столбцов 4 и 5 плюс небольшой запас. Минимальное допустимое количество абитуриентов выбиралось приблизительно на 100 человек меньше X max . Таким образом, мы получили все показатели для оптимизации распределения абитуриентов по направлениям подготовки в соответствии с методикой решения задачи оптимального распределения ресурсов в условиях неопределенности [4].

Функционал (1) является мультимодальным, и, кроме того, каждый его экстремум достигается в точке компромисса в смысле Парето. Это связано с тем, что в нечетко-множественной постановке любая ЗМП становится задачей многокритериальной (векторной) оптимизации в связи с тем, что ЦФ и элементы системы ограничений – равноправные компоненты задачи (1). Другими словами, в нечеткой постановке ЗМП между ее элементами стирается математическое различие и задача должна решаться в смысле оптимума по Парето. Последнее означает, что задача может иметь множество решений, в одинаковой степени удовлетворяющих всем условиям. Поиск глобального экстремума мультимодальной функции сопряжен с известными трудностями. Наиболее эффективными способами решения таких задач в настоящее время являются методы метаэвристической оптимизации. Для поиска наилучшего распределения абитуриентов по направлениям мы воспользовались методом «волчьей стаи» (Grey Wolf Optimizer) [5].

Решение задачи (1) дало следующее оптимальное распределение абитуриентов по направлениям подготовки, учитывающее все указанные ограничения:

ɏ 0 = {450 435 509 498 532 77 621 680 355 915}.

Общее количество первокурсников равно 5 072, что на 538 человек меньше максимально допустимого числа, равного сумме элементов X max .

Вычитая из данных четвертого столбца таблицы 1 значения оптимального количества абитуриентов по каждому представленному направлению подготовки, получаем превышение числа бюджетных мест над оптимальным приемом абитуриентов:

Δ ɏ = {330 15 –14 17 8 13 496 30 35 2 378}.

Отсюда следует, что по первому, седьмому и десятому направлениям подготовки (см. таблицу 1) целесообразно сократить контрольные цифры приема абитуриентов, при этом по другим направлениям обучения специалистов с ВО, в частности «Строительство», уместно их увеличение. Отметим, что этот результат подтверждает адекватность модели, поскольку вывод об изменении объемов бюджетного финансирования можно сделать и на основании анализа данных, приведенных в таблице 1.

Математическая модель для оптимального распределения молодежи в возрасте 15–17 лет по направлениям подготовки с использованием нечетко-множественного подхода позволила подтвердить выводы, сделанные ранее [6]. Система подготовки квалифицированных специалистов и рабочих кадров региона для эффективного развития приоритетных видов экономической деятельности нуждается в существенных изменениях, связанных в первую очередь с увеличением контрольных цифр приема абитуриентов в средних профессиональных образовательных организациях и их корректировкой по ряду направлений в вузах. Также необходимы актуализация профессиональной ориентации в общеобразовательных учреждениях (престижность получения рабочей профессии), информирование обучающихся о реальной ситуации на рынке труда, создание модели взаимодействия социальных институтов образования и рынка труда, соответствующей современным требованиям Республики Крым и учитывающей ее опережающее развитие.

Ссылки:

• 1.    Полищук Е.А., Клевец Н.И. Моделирование кадровых потребностей реального сектора экономики Республики Крым // Теория и практика общественного развития. 2016. № 9. С. 45–48.

• 2.    Беллман Р. Принятие решений в расплывчатых условиях // Беллман Р., Заде Л. Вопросы анализа и процедуры принятия решений. М., 1976. С. 172–215.

• 3.    Зак Ю.А. Принятие решений в условиях нечетких и размытых данных: Fuzzy-технологии. М., 2013. 352 с.

• 4.    Клевец Н.И. Оптимальное распределение ресурсов в условиях неопределенности // Научный вестник: финансы, банки, инвестиции. 2016. № 1 (34). С. 118–123.

• 5.    Mirjalili S., Mirjalili S.M., Lewis A. Grey Wolf Optimizer // Advances in Engineering Software. 2014. Vol. 69. P. 46–61.

• 6.    Полищук Е.А., Клевец Н.И. Указ. соч.