Оптимизация режима формирования антифрикционного покрытия при алмазном выглаживании с применением ультразвуковой энергии

Применение ультразвука при поверхностной обработке деталей отражено в больших количествах работ [1-8]. В этих работах показано, что использование ультразвука при обработке деталей обеспечивает снижение шероховатости обработанной поверхности, повышение микротвердости поверхностного слоя, устранение множества дефектов поверхностного слоя и, как следствие, ультразвуковая обработка способствует повышению износостойкости деталей. В работах [9, 10] впервые показано, что ультразвуковое алмазное выглаживание можно эффективно использовать для формирования диффузионного антифрикционного покрытия. Формированию покрытия способствует то, что в процессе ультразвуковой обработки возникает пластическая деформация обрабатываемой поверхности, а в зоне контакта с алмазным наконечником возникает высокая температура. Нанесение покрытия методом ультразвуковой поверхностной обработкой обеспечивает надежное диффузионное закрепление антифрикционного материала на поверхности деталей, устраняет возможность его растрескивания и отслоения при высоких локальных нагрузках на поверхность и при колебании температуры. Поэтому важной задачей является оптимизация режима формирования антифрикционного покрытия на основе применения ультразвуковой поверхностной обработки.

МЕТОДИКА ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ

Для проведения экспериментальных исследований использовалась методика рационального планирования экспериментов. Осуществлялся полный факторный эксперимент на двух уровнях 2⁴. В качестве варьируемых факторов приняты основные влияющие на результаты обработки факторы: радиус округления рабочей части индентора r (мм), статическое усилие прижима индентора к обрабатываемой поверхности Р (H), поперечная подача индентора S (мм/об) и частота вращения образца n (мин^-1). Параметры ультразвуковых колебаний использовались постоянными. В качестве показателей обработки приняты глубина диффузии, шероховатость и микротвердость получаемой поверхности.

Условия и средства проведения эксперимента

Эксперимент проводился на установке собранной на основе токарно-винторезного станка 16К20. Для осуществления ультразвуковой обработки использовался генератор УЗГ 10 – 22 и магнитострикционный преобразователь ПМС15А – 18.

В качестве твердой смазки использовался порошок графита. Экспериментальные образцы – ро лики 32X52 II ГОСТ 22696-2014 буксового подши пника серии 36-42726Е2М (ОСТ 18855-94).

На рис. 1 показаны способ и устройство, лика антифрикционного покрытия [11, 12].

предназначенное нанесения на поверхность торца ро

• 1    - патрон токарного станка;

• 2    - втулка;

• 3    - уплотнительное кольцо;

• 4    - обрабатываемая деталь;

• 3    - суппорт токарного станка ;

• б    - ультразвуковой пьезокерамический преобразователь;

• 7    - сферический индентор;

й - обрабатываемый торец детали 4;

S - отверстие для подачи сжатого воздуха под давлением q;

• 10    - упор.

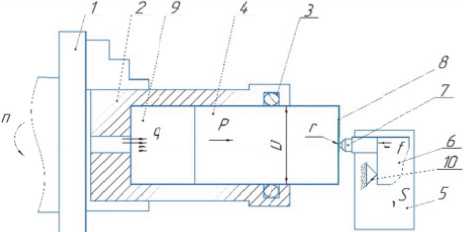
Рис. 1. Схема установки для нанесения на поверхность торцов роликов твердого антифрикционного покрытия

Деталь 4 , представляющая собой металлический ролик подшипника с наружным диаметром D=32 мм, установлена во втулку 2 и торцом 8 поджимается сжатым воздухом 9 к алмазному индентору 7, имеющему сферический наконечник радиусом r . Давление сжатого воздуха в полости 9 подбирается так, чтобы сила прижима ролика с алмазному индентору составляла заданную величину P, Н . Уплотнительное кольцо 3 препятствует утечки воздуха и создает трение, необходимое для вращения детали 4. На торец 8 детали наносится графитовая смазка.

Включается вращение детали 4 , алмазный индентор 7 получает ультразвуковые колебания с амплитудой А=10 мкм и частотой f=20 МГц, и перемещается в радиальном направлении детали 4 с поперечной подачей S . Под действием ультразвуковых колебаний индентора 7 осуществляется диффузия антифрикционного материала в поверхность обрабатываемого торца, упрочняется поверхностный слой детали и снижается шероховатость поверхности.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

В табл. 1 приведены значения варьируемых факторов.

Таблица 1 – Варьируемые факторы область их определения

Наименование фактора, размерность	Натуральные границы области определения
	нижняя	верхняя
Статическое усилие Р, H	100	300
Поперечная подача S, мм/об	0,07	0,14
Радиус алмаза г, мм	2	4
Частота вращения n z , мин-1	500	1500

В работах [9, 10] приведены уравнения регрессии, которые получены в результате эксперимента при исследовании зависимости трех параметров оптимизации : глубины диффузии z (мм), шероховатости обработанной поверхности Ra (мм) и микротвердости обработанной поверхности HV от варьируемых факторов:

z(r, P, S, n) = 0,0021 ^. r ^{(-1,78) .} P ^{0,485 .} S ^{(-0,9 ) .} n ^(-0,212), (1)

Ra(r, P, S, n) = 0,0008 ^. r ^{(-0,32) .} P ^{(-0,25) .} S ^{0,55 .} n ^0,11, (2)

HV(P, S, r, n) = 1530 ^. P ^{0,09 .} S ^{(-0,1) .} r ^{(-0,21) .} n ^(-0,15), (3) где r – радиус округления вершины алмазного индентора, мм; P – сила прижима алмазного индентора к обрабатываемой поверхности, Н; n – частота вращения образца, об/мин; S – поперечная подача алмазного индентора, мм/об.

В качестве примера на рис. 2 представлены зависимости глубины антифрикционного покрытия, шероховатости и микротвердости обработанной поверхности от влияющих факторов.

Построение математических моделей на основе уравнений регрессии позволяет на практике использовать оптимальные условия ультразвукового нанесения диффузионного покрытия. В качестве метода оптимизации обычно используются методы линейного программирования. К числу таких методов относится симплекс-метод, который позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода заключается в том, что вычисления начинаются с базисного решения, а затем ведется поиск решений, улучшающих значение целевой функции. Это возможно только в том случае, если возрастание переменной

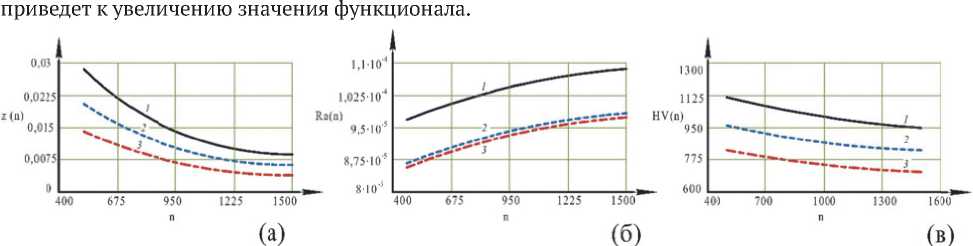
Рис. 2. Зависимость глубины диффузии z (мм) материала покрытия (а), шероховатости Ra , мкм (б) и микротвердости HV (в)поверхности от частоты вращения заготовки n (мин^-1) при 1 – минимальных, 2 – средних и 3 – максимальных значениях других факторов

Алгоритм решения задачи оптимизации симплекс-методом включает:

• -    определение условий осуществления процесса

• -    определение системы неравенств

• -    выявление принятых ограничений

• -    определение области допустимых значений оптимизируемого процесса, из которых затем выбираются такие значения, которые обеспечивают min (max) критерия оптимизации.

В качестве критерия оптимизации процесса примем обеспечение максимальной производительности. Производительность процесса алмазного выглаживания с ультразвуковой обработкой определяется значениями поперечной подачи S и частоты вращения детали n . При этом основное время Т , мин равно : ^о

т =--е 0 Sh ,

где l_p – величина перебега инструмента, м за пределы диаметра детали D , м.

Производительность – величина обратная времени. Используя обратную величину T_o и производя ее логарифмирование для приведения к линейному виду, получим целевую функцию в виде:

F_c ( ln S, ln n) = f ( ln S + ln n) _max.                                       (4)

Одним из ограничений оптимизируемого процесса является глубина диффузии, которая должна быть не меньше заданной величины z. Подставляя указанное значение в равенство (1), получим первое неравенство:

z ≥ 0,0021 . r (-1,78) . P 0,485 . S (-0,9 ) . n (-0,212) .

Искомые параметры переносим в левую часть, а все остальные значения – в правую:

с (-03) . „(-0,212) < 2

0 0021 ■ rC"1'78) ■ р 0,485 .

Из равенств (1)–(3) следует, что уменьшение значения радиуса округления индентора r и возрастание значения силы прижима индентора к обрабатываемой поверхности P благоприятно влияет на все показатели обработки. Поэтому при обработке используем следующие значения этих факторов: r=2 мм , P=300 Н . Подставляя эти значения в предыдущее равенство и производя его логарифмирование для приведения к линейному виду, получим:

4,25 ln S + ln n ≤ -4,72 ln z – 21,86.                                 (5)

Используя ограничения по шероховатости Ra и по микротвердости HV обработанной поверхности, а также ограничения режима обработки, принятые в экспериментальных исследованиях, подобно (5) получим систему неравенств, составляющую математическую модель для оптимизации режима обработки.

Обозначим X = ln S , Y = ln n . Тогда математическая модель примет вид:

Y1 ≤ –4,72 ln z – 21,86 – 4,251X;(6)

Y2 ≤ 9,09 ln Ra + 79,81 – 5 X.(7);

Y3 ≤ –6,67 ln HV + 51,34 – 0,67 X;(8)

Y4 ≤ 7,313;(9)

Y5 ≥ 6,215;(10)

X ≥ –2,659;(11)

X ≤ –1,966;(12)

Fc (X, Y) = f (X + Y)max .(13)

Подставляя в эту систему неравенств значения, ограничивающие глубину диффузии z , шероховатость поверхности Ra и микротвердость HV , несложно определить значения, соответствующие целевой функции. Например, для торца ролика буксового подшипника за минимальное значение глубины диффузии примем z=0,02 мм, так как допуск на длину ролика составляет 20 мкм, следовательно, износ ролика больше этой величины не допустим. Требуемая шероховатость поверхности торца ролика составляет не более Ra=0,0001 мм. Минимальное значение микротвердости торца ролика примем равным HV=1000.

Для этих ограничений на рис. 3 заштрихована допустимая область значений X и Y, синей сплошной линией показана целевая функция, касательная к верхней точке области допустимых значений.

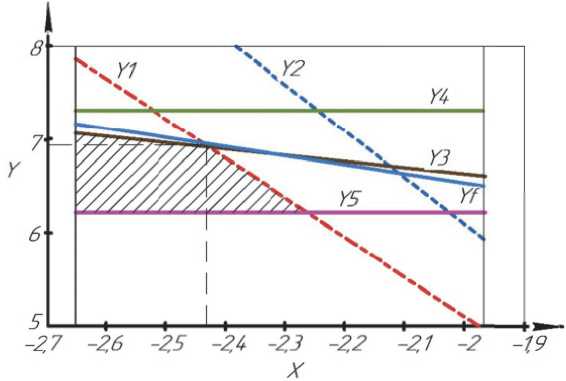
Рис. 3. Графическая интерпретация решения задачи оптимизации режима ультразвуковой обработки торца ролика буксового подшипника

Значения X = –2,43 , Y = 6,95 , соответствующие этой точке, и определяют оптимальные значения искомых величин. Переходя от логарифмов к натуральным значениям искомых параметров, имеем: S = 0,09 мм/об, n = 1000 мин^-1.

Таким образом, оптимальными условиями обработки торцев роликов буксовых подшипников с применением ультразвуковой энергии по критерию максимальной производительности являются: частота вращения детали n = 1000 мин^-1 ; поперечная подача ультразвукового инструмента S=0,09 мм/об , радиус округления индентора r = 2 мм , сила прижима индентора к обрабатываемой поверхности P = 300 Н .

ЗАКЛЮЧЕНИЕ

Выполненные исследования позволяют с максимальной производительностью осуществлять процесс формирования антифрикционного покрытия ультразвуковой поверхностной обработкой деталей. В частности, при заданных ограничениях: глубины диффузии, равной z ≥ 0,02 мм, требуемой шероховатости поверхности, обработанной поверхности Ra ≤ 0,1 мкм и микротвердости поверхностного слоя HV ≥ 1000 , оптимальными условиями процесса обработки являются: частота вращения детали 1000 мин^-1; поперечная подача ультразвукового инструмента 0,09 мм/об, радиус округления индентора 2 мм, сила прижима индентора к обрабатываемой поверхности 300 Н. Практическое применение проведенных исследование позволит повысить эксплуатационные характеристики, такие как надежность и долговечность при производстве тяжело нагруженных узлов и деталей, например, роликов буксовых подшипников