Оптимизация режимов резания механической обработки с применением системы Ansys
Автор: Мурадымов А.М., Гисметулин А.Р.
Журнал: Мировая наука @science-j
Рубрика: Основной раздел
Статья в выпуске: 5 (38), 2020 года.
Бесплатный доступ
В статье представлены результаты теоретического определения и моделирования процесса концевого фрезерования с применением цилиндрической фрезы и результаты неупругих деформаций детали при различных режимах обработки деталей: ширины и угла наклона винтовой канавки. Рассмотрены модели статики процесса фрезерования в двухмерной и трехмерной постановке на основе конечно-элементного анализа взаимодействия инструмента и обрабатываемой заготовки с использованием возможностей программного комплекса Ansys. В качестве инструмента была выбрана цилиндрическая фреза диаметром 5 мм и 8 мм из быстрорежущей стали, а заготовкой является формообразованный лист из сплава алюминия «1163». Приводится таблица зависимости сил резания от изменяемых величин диаметра и угла наклона винтовой канавки. По сравнению результатов моделирования с теоретическими выводами и существующими результатами экспериментов других авторов была подтверждена работоспособность программы Ansys при моделировании и анализе деформаций вызванных действием сил резания процессов концевого фрезерования.
Концевое фрезерование, моделирование, конечно-элементный анализ, силы резания, ansys, деформации резания, форма образованный лист, обшивка самолета
Короткий адрес: https://sciup.org/140293994
IDR: 140293994 | УДК: 621.914.1
Текст научной статьи Оптимизация режимов резания механической обработки с применением системы Ansys
В самолете практически нет прямых деталей. Для придания нужной кривизны используют набор форм для обтяжки на специальном прессе (рис.1). Деталь устанавливают в пресс, прижимают ремнями и по программе прикладывают усилия, необходимые для её формообразования.
Задав необходимый изгиб для заготовки, можно вырезать контур.
Обшивки малого размера можно вырезать с помощью лазера. Крупногабаритные обшивки самолета (форма образованные листы), обрабатывают по программе на пятиосевом фрезерном станке с ЧПУ. Изготовленные обшивки крыла контролируются на специальном стенде с набором шаблонов. Отклонение 14-метровых обшивок крыла должно быть не более +/- 1 мм (рис.2).

Рисунок 1 - обтяжные пуансоны

Рисунок 3 - стенд с набором шаблонов
При обработке обшивки под действием силы резания возникают пластические деформации в конструкции детали и упругие деформации инструмента, что существенно снижает точность обработки. Минимизация возникающих деформаций за счёт режимов резания приводит к тому, что увеличивается длительность обработки. Компьютерное моделирование процессов резания с применением CAE систем позволит определить оптимальные значения режимов резания.
В работе предлагается использовать модули программы Ansys, для моделирования деформаций в обшивки из сплава алюминия «1163».
Оптимизация технологических условий обработки деталей включает решение различных технологических, экономических, конструкторских и организационных задач и при проектировании технологического процесса (операции, перехода) оптимизация базируется на ранее накопленном производственном или научно-экспериментальном опыте, систематизированном в виде нормативов, стандартов, рекомендаций [1,2]. Используемые при оптимизации операций резания издания общемашиностроительных нормативов являются довольно грубым приближением к действительности, а оценка рекомендуемых режимов резания лежит в широком доверительном интервале. В связи с этим в решение задач повышения эффективности фрезерования на основе оптимизации параметров технологических операций входит:
-
• подбор оптимального диаметра и угла наклона винтовой канавки;
-
• подбор оптимальной величины подачи;
-
• оценка величин пластических деформаций детали;
Ниже (рис.4) приведена схема, используемая в работе [1], поясняющая расчёт срезаемого слоя и сил резания при концевом фрезеровании. На схеме режущая кромка представлена при обработке уступа с шириной B (размер, параллельный оси фрезерования) и глубиной резания t (размер перпендикулярный оси). Кинематическими параметрами являются величины: частота вращения фрезы n , подача S .
Система координат XYZ с началом в точке 2 имеет ось X по направлению оси фрезы, ось Y по направлению радиуса, ось Z по направлению скорости резания.
Режущая кромка зуба, согласно схеме работы [1] разделена на три участка: винтовая кромка 12 с углом наклона к оси ω 0 на цилиндрической части, радиусная кромка 23 с радиусом г ^ 0, торцевая кромка 34 под вспомогательным углом в плане <р 1 .
Наибольшая толщина среза на винтовой канавке в точке определяется формулой и графиком (рис.4):
cl = sz srni^o, где: Sz - подача на зуб фрезы, мм/зуб; гр0- угол поворота фрезы.
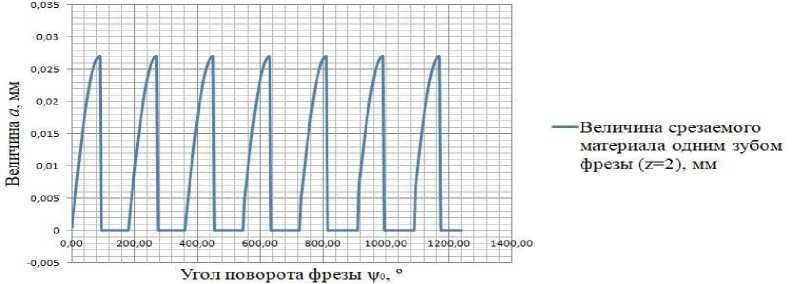
Рисунок 4 - Зависимость между величинами подачи и угла поворота фрезы
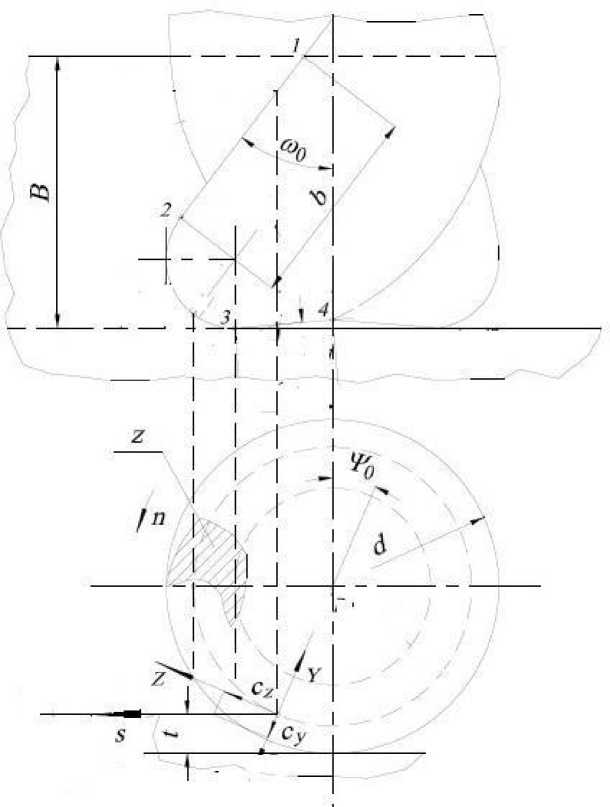
Рисунок 5 - Схема расчёта кинематических параметров и сил резания
Силовые параметры, изображённые на рис.5., по отдельности для каждой режущей кромки, но задача определения сил возникающих при чистовой обработке, допускает рассмотреть величины сил, возникающих на кромке 12, при условии b ^ В. [1]
Результирующая сила стружкообразования направлена под углом действия ω к скорости резания и определена через касательную силу в плоскости сдвига Рт и определяется выражением:
рт _ т р ab
sin(^) cos(^+«) sln(p) cos(p+to)> где: тр - касательные напряжения в плоскости сдвига.
В результате для вычисления касательной и нормальной составляющих силы на передней поверхности инструмента, определяются из геометрических соотношений:
Ег = /?csinE£ko + у); Рп = Rc cos((o + у)
Составляющие силы стружкообразования для осей Y и Z имеют вид:
Rcz =Rccosm;RCy = Rcsinw (2)
Используя результаты моделирования в работе [2], принимаем гипотезу, что максимальное значение контактного давления распределяется по всей режущей кромке одинаково, выражая через нормальную силу напряжения и площадь контакта:
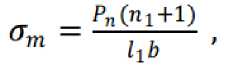
где: п1=1 - показатель степени выражения для эпюры контактного давления; 11 - длина контакта стружки.
Максимальное значение контактного напряжения распределяется по длине дуги AB и определяется глубиной подминаемого слоя h≤Δ. Результирующая сила, действующая по всей длине дуги AB , определяется с помощью Р т = о т ЬА В, которая направлена под углом
^ к оси Y. При разложении результирующей силы вдоль осей Y,Z получаются выражения:
P mz Ртг^шф; Р ту R m COS^
Нормальная сила Р 2 на площадке износа h z определяется через площадь контакта и контактное давление, а касательная сила F 2 рассчитывается через средний коэффициент трения:
Р 2 = (У т h z b; F 2 = P 2 f tr (5)
На изображенной схеме (рис. 5) лезвие зуба концевой фрезы оказывает силовое воздействие на обработанную поверхность по площадке износа, равно величиной h z , по дуге режущей кромки - равномерно-распределённое контактное давление У т . Величина этого давления является одним из выходных параметров расчётного алгоритма. Из этого следует, что величина использована для моделирования деформаций листовых деталей.
Силы резания при концевом фрезеровании является отношение величин ширины и глубины резания на величины действующим на передней поверхности Rcz , дуге округления кромки Pmz и на задней поверхности зуба фрезы F2, которые являются одними из составляющих расчетных параметров является главной (тангенциальной) составляющей силы резания на цилиндрической части, которая определена суммированием по соответствующим направлениям сил:
Р общ = R cz + P mz + F 2 (6)
Для вычисления оптимальных режимов резания при фрезерования контура обшивки, будет рассчитано и смоделировано по трем фрезам, но с разной величиной подачи на зуб (S Z =0.03;0.07мм/зуб) и разным углом винтовой канавки ω°(таб. 1) и постоянным вращением шпинделя n=12000 мин-1, z =2.
Таблица 1- Экспериментальные данные
|
№ |
Ø |
Глубина срезаемого слоя, мм |
ω° |
S z |
||
|
1 |
8 |
1 |
45 |
0,03 |
0,05 |
0,07 |
|
2 |
5 |
1 |
45 |
0,03 |
0,05 |
0,07 |
|
3 |
5 |
1 |
0 |
0,03 |
0,05 |
0,07 |
Допустимое упрощение детали, построение сетки для обеспечения снижения времени расчёта представлено на рис.6.
Рисунок 6 - Упрощение геометрии при подготовке к эксперименту
На рис. 7 представлены значения параметров материалов и граничных условий.
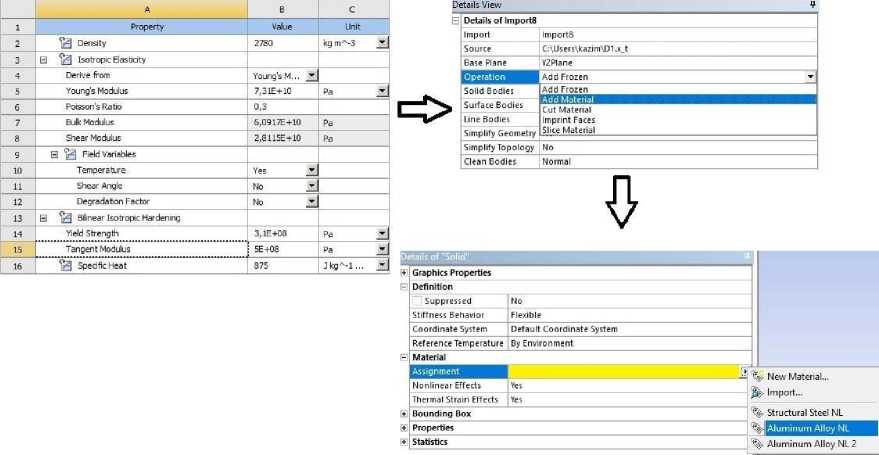
Рисунок 7 - Исходные данные для проведения моделирования
Расчетные значения сил резания по зависимостям (1-9) представлены в таблице 2.
Таблица 2 - Исходные данные для моделирования
|
№ |
Величина глубины фрезерован ия t , мм |
Ø |
ω° |
S z |
Нормальная сила на дуге округления кромки Pmz , Н |
Нормальная сила на передней поверхности Rcz , Н |
Касательная сила на задней поверхности ^, Н |
|
1 |
1 |
5 |
45 |
0,03 |
1,31 |
2,58 |
1,88 |
|
2 |
0,05 |
2,18 |
4,3 |
3,13 |
|||
|
3 |
0,07 |
3,05 |
6,02 |
4,38 |
|||
|
4 |
1 |
5 |
0 |
0,03 |
1,22 |
2,65 |
1,72 |
|
5 |
0,05 |
2,03 |
4,41 |
2,86 |
|||
|
6 |
0,07 |
2,84 |
6,18 |
4,01 |
|||
|
7 |
1 |
8 |
45 |
0,03 |
3,21 |
6,65 |
4,72 |
|
8 |
0,05 |
5,35 |
11,08 |
7,86 |
|||
|
9 |
0,07 |
7,49 |
15,51 |
11,01 |
Занесение сил резания прикладываемых к срезу слою определяется по вектору направления каждой из сил. В результате формируется вектор результирующей силы, см. рис. 8.
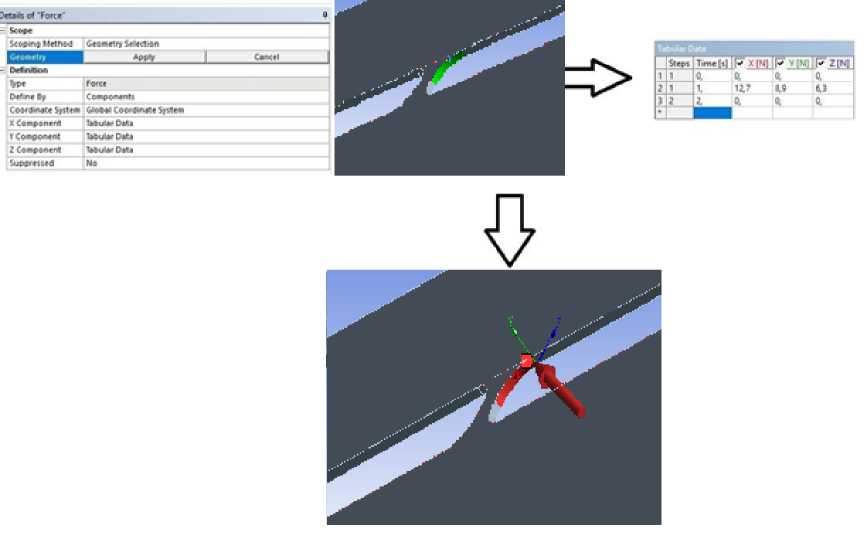
Рисунок 8 - Задание точек крепления детали и действия силы резания
Расчёт деформаций показал, что величины деформаций в некоторых случаях превышают условный предел текучести алюминиевого сплава 1163. Это приводит к пластическим деформациям, см. рис. 9
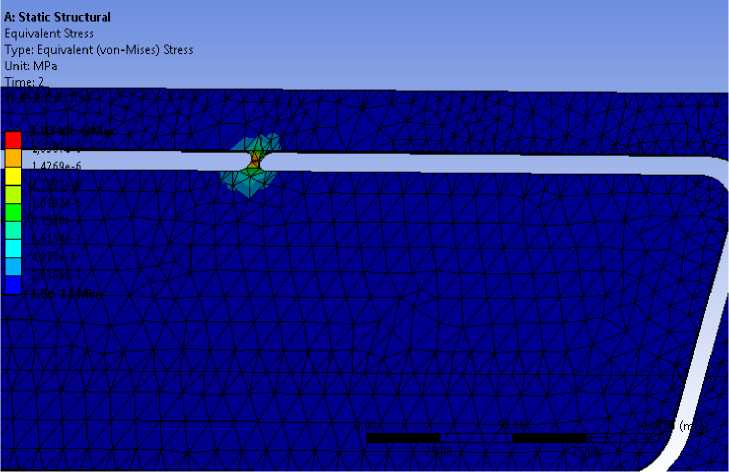
Рисунок 9 - Величины деформаций стенки детали в процессе резания
Результаты компьютерного моделирования были занесены в таблицу 3, в которой дополнительно приведены расчетные и экспериментальные величины упругих деформаций.
Таблица 3 - Результаты компьютерного, математического и натурного экспериментов
|
Номер экспери мента |
Сила резания ^ общ , Н |
Максимальная величина деформаций Δ при компьютерном эксперименте, мм |
Максимальная величина деформаций Δ при математическом эксперименте, мм |
Максимальная величина деформаций Δ при натурном эксперименте, мм |
|
1 |
5,77 |
0,00865 |
0,009809 |
0,00953 |
|
2 |
10,23 |
0,015345 |
0,017393 |
0,01624 |
|
3 |
13,45 |
0,020175 |
0,022865 |
0,020195 |
|
4 |
5,58 |
0,00837 |
0,009486 |
0,00856 |
|
5 |
9,3 |
0,01395 |
0,01581 |
0,01489 |
|
6 |
13,03 |
0,019545 |
0,022151 |
0,01987 |
|
7 |
14,58 |
0,02187 |
0,024786 |
0,02258 |
|
8 |
24,29 |
0,036435 |
0,041293 |
0,04216 |
|
9 |
34,01 |
0,051015 |
0,057817 |
0,05456 |
Заключение
Разработана методика расчёта сил при фрезеровании концевыми фрезами обшивки из сплава алюминия «1163».
Сформированная математическая модель позволяет определять допустимые значения пластических деформаций обрабатываемой детали. Получены зависимости влияния режимов резания на точность обрабатываемой детали, которые позволяют определять их оптимальные значения по критериям деформации детали и требуемой точности обработки.
Список литературы Оптимизация режимов резания механической обработки с применением системы Ansys
- Грубый С.В.. Зайцев A.M. Обоснование условий фрезерования карманов в корпусных деталях из алюминиевых сплавов/' Наука и образование. МГТУ им. Н.Э. Баумана. Электрон, жури. Режим доступа: http: engineering-science.ru/doc/709770.html (дата обращения 19.02.2019).
- Старков В.К. Фишка и оптимизация резания материалов. М.: Машиностроение, 2009.


