Оптимизация симметричного профиля методом сопряженного градиента

Метод сопряженного градиента может иметь непрерывную или дискретную формулировку. Непрерывная формулировка представлена в работах [1, 2], она обладает более строгим обоснованием граничных условий и не зависит от решателя уравнений движения. Дискретная формулировка представлена в [3, 4], сравнение непрерывного и дискретного подходов дано в [5]. В данной работе используется непрерывная формулировка. В статьях [1, 2] прямая задача и сопряженные уравнения решались при помощи различных разновидностей метода искусственной вязкости (диссипации) [6]. В представленной работе для этой цели используется метод поправок давления алгоритм SIMPLE [7]. Этот алгоритм хорошо себя зарекомендовал и широко используется в коммерческих CFD пакетах.

Формулировка метода. Необходимо минимизировать функцию цели I(w,s) в соответствие с заданными функциями ограничений R(w,s)=0 , где w(s) – переменные поля течения, s – проектные переменные, описывающие форму тела. Функцией цели, например, может быть лобовое сопротивление тела, подъемная сила или заданное распределение давления. Функциями ограничений являются уравнениями движения. Двумерное стационарное течение вязкого несжимаемого газа описывает система уравнений Навье-Стокса. Для удобства обозначим декартовы координаты x 1 , x 2 , а компоненты вектора скорости u 1 , u 2 , также будем подразумевать суммирование по повторяющимся индексам i (i=1,2) . Тогда уравнения Навье-Стокса могут быть записаны как:

где

д f    д f'

— 0

^д xi ^д x    в области D,

J,—\

ui pu, ui + pSi, f. f

v

;

где B B ξw – контур тела в вычислительном пространстве.

Выражение для вариации функции цели имеет вид:

SI — J SM (w, s) dB

B ^ w

p u 2 u + pS_i2

^j — Ц

д u,    ^д u.

— + j

дXj   дx,

к j i 7

Sj —

0, если i * j

1, если i — j ^;

p – давление; ρ – плотность; µ - вязкость.

За переменные поля течения w(s) принимается вектор w=(p,u 1 ,u 2 )^T . Для вывода сопряженных уравнений векторное уравнение (1) необходимо представить в вычислительном пространстве с системой координат ξ 1 , ξ 2 такой, что контур исследуемого тела лежит на оси ξ 1 :

д F- д F

— 0 д^  д^

Уравнение (3) умножим на вектор множителей Лагранжа, ψ^T=(ψ 1 , ψ 2 , ψ 3 ) в каждой точке рассматриваемой области D ξ , проинтегрируем по ней и вычтем из выражения (5), в результате получим:

SI — JSM(w, s)dB^ - Jn^T (SFt- SF" )d!B^ +

^B 5 w                       B e

+ J|y (SF-- sf ' )d*D«,

D6 де i

vv где i ij j ; i ij j ^,

Получим вариацию

( дx2

. д^2

S —

-ax, к д^д функций ограниче-

где n ^ξ - компоненты вектора внешней нормали к границе области B B ξ в вычислительном пространстве. Исходя из предположения, что на внешней границе рассматриваемой области вариации потоков вследствие изменения формы тела равны нулю, можно записать:

SI — J [SM - n^T(sf t - sf, )]dBe +

B ^ w

ний δR(w,s) . Так как в вычислительном пространстве форма тела и соответственно область D ξ остаются неизменными при вариациях формы в физическом пространстве, то для любой точки вычислительной области D ξ можно записать:

+ J|^ (S-' SF;dlDe + + JX (SF'"-SF'"^1.

ж _д2й-aj-F.—0 д^,      8^,

Необходимо найти такие ψ , чтобы первые два интеграла выражения (6) обратились в нуль. Таким образом, сопряженные уравнения и соответствующие граничные условия можно записать в форме:

Запишем вариации для потоков в следующем виде:

SFi— 5Fn+ 5FH1 SFi — 5FV + SF^vi

где вариации с индексом I являются вкладами, связанными с изменением переменных поля течения δw , а с индексом II – вклады, связанные с изменением формы тела δs .

Рассмотрим функцию цели I , которую можно представить как интеграл по границе B B ξw :

I — J M ( w, s ) dB ^

B ^ w

JUT(SF""SF" "dD1 —0

De д i

J[SM - ni^T (SF,- SF- jdB; — 0.

_ B w

Определив вектор множителей Лагранжа из уравнений (7), можно найти вариацию функции цели по формуле:

S ' — J ! [ ( S F'- -S F 'v^ dD e

Вариации потоков представим как:

v

S F„   ^F S s S F v = ^F- S s

II iII i оs

,,

9F где i и i определяются численно, варь-ds ируя соответствующую компоненту вектора проектных переменных s при неизменном поле течения. Тогда градиент функции цели есть:

g цд/ faF._a F i D ₅ a^ i

^^^^™

v

(d s d s J

dD ^

.

Пользуясь методом наискорейшего спуска, получим: δs=-αG , где α – положительное малое число, которое определяется в ходе численных экспериментов.

Как правило, градиент G не обладает той же гладкостью, что и исходный контур, поэтому алгоритм оптимизации может оказаться неустойчивым. Во избежание этой проблемы в работе [2] предлагается з а менить градиент G сглаженным градиентом G , который получается в результате решения неявного сглаживающего уравнения:

G

^^^^^^^e

5  5 G

--e--= G a^i a^i где e – параметр, влияющий на степень сглаживания градиента. Таким образом, для вариации вектора проектных переменных можно записать:

^S s = -« ^G . (10)

Прямая задача решается для вязкой несжимаемой жидкости методом контрольного объема при помощи алгоритма SIMPLE [7], сопряженные уравнения решаются при помощи адаптированного алгоритма SIMPLE. На рис. 1 представлена блок-схема работы алгоритма оптимизации.

Результаты и обсуждение. Постановка задачи: минимизация лобового сопротивления симметричного профиля при заданной площади и хорде. В качестве исходного профиля был взят симметричный профиль. На рис. 2 изображены геометрические характеристики этого профиля.

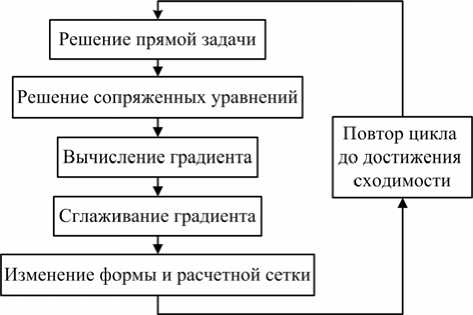
Рис. 1. Блок-схема работы алгоритма оптимизации

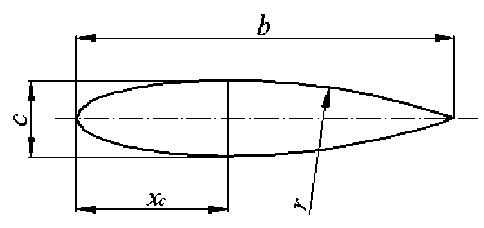
Рис. 2. Исходный профиль Е–004020

Носовая часть – это половина эллипса с полуосями x c =0,4b и c=0,2b , хвостовая – дуги окружностей, это есть профиль серии Е– 004020. Число Рейнольдса составляет Re=66575 , то есть обтекание можно считать ламинарным. Проектными переменными являются координаты узлов расчетной сетки, лежащие на контуре профиля. Согласно формулировке задачи функцию цели можно записать:

I =-f 5 „(»„ p - Oj! H+ cVp

B_

V ^ V^

( V 0 J

, где V – площадь текущего профиля; V0 – площадь исходного профиля Е–004020; CV – весовой коэффициент, который вводится для обеспечения устойчивости алгоритма оптимизации.

На рис. 3 представлен исходный профиль Е–004020 и оптимизированный на расчетной сетке 200х30, число итераций N=200 . На том же рисунке приведены значения относительного изменения лобового сопротивления ΔX и относительного изменения площади профиля ΔS .

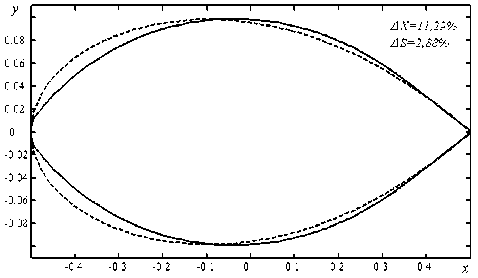
Рис. 3. Профиль, полученный в результате оптимизации (сплошная линия) и исходный профиль Е – 004020 (пунктирная линия)

В результате оптимизации был получен локальный минимум и сопротивление профиля снизилось на 11,29% при заданной площади. Эта задача хорошо демонстрирует эффективность метода сопряженного градиента. Полученные результаты можно использовать для выбора формы симметричного профиля для несжимаемого ламинарного течения.