Оптимизация слаломной траектории с учетом наклона лыжника

Биомеханические проблемы горнолыжного спорта постоянно привлекают внимание исследователей; в публикациях последних лет горнолыжник моделируется в виде достаточно сложной стержневой системы [1-3]. Однако многие эффекты, возникающие при прохождении слаломной трассы, могут быть исследованы на более простых моделях горнолыжника. Ранее в работах авторов [4-8] лыжник моделировался материальной точкой, движущейся по слаломной траектории, определяемой как осредненный след лыж на криволинейном горном склоне. В данной работе эта модель несколько усложнена, что позволило учесть наклон лыжника в сторону вогнутости траектории лыж и приблизить к реальной расчетную траекторию движения центра масс системы лыжник-лыжи. Так как в момент обхода шеста траектория лыж проходит в непосредственной близости от него, происходит столкновение корпуса лыжника с шестом. Предполагается, что шест при наезде лыжника безынерционно отклоняется от вертикального положения и не оказывает сопротивления движению лыжника.

Модель движения системы лыжник–лыжи

Система лыжник-лыжи представляется материальной точкой M , жестко

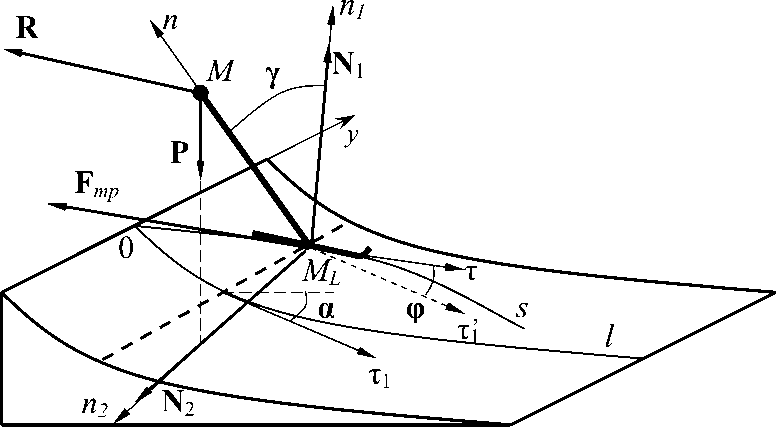
Рис. 1. Геометрия элемента слаломной траектории и силы, действующие на систему лыжник–лыжи

связанной с невесомым стержнем MM_L (рис. 1). Масса материальной точки m равна суммарной массе лыжника и лыж. Невесомый стержень имеет длину h , равную расстоянию от центра масс системы до лыж, и составляет с нормалью к склону переменный угол γ [6]:

Y = arctg

f          1

( r e g cos(a) )

где V – скорость лыжника, r_C – радиус кривизны траектории центра масс, g – ускорение свободного падения, α – угол склона горы в данной точке.

Склон горы представляется как часть поверхности цилиндра радиуса R_с , в верхней части которой угол склона равен α₀ . В произвольной точке склона

a( l)=а о -    , где l – расстояние, пройденное лыжником по линии наибольшего ската в произвольной точке ML слаломной траектории.

Слаломная трасса определяется двумя рядами шестов, расположенных по обе стороны от линии наибольшего ската в шахматном порядке. Период трассы L , а расстояние шестов от средней линии наибольшего ската равно a . Так же, как и в работе [4], уравнение траектории центра масс системы лыжник–лыжи представляется полиномом шестого порядка. Параметры оптимизации этой траектории – угол входа в поворот фe и радиус кривизны траектории центра масс be при обходе лыжником шеста. В настоящей работе траектория движения центра масс задается таким образом, что ее период равен L , а амплитуда aC определяется выражением ae = a - l sin(ym ),

где γ _m – максимальный угол наклона лыжника, определяемый по формуле (1) при r C = b C .

В исследуемой модели движения приняты следующие допущения. Предполагается, что расстояние от центра масс до лыж постоянно ( h = const), и центр масс движется по цилиндрической поверхности. Целью данного исследования является оценка влияния наклона лыжника на оптимальную траекторию лыж и на время прохождения трассы.

Система сил и дифференциальные уравнения движения центра масс

При движении лыжника по слаломной траектории на него действуют следующие силы: сила тяжести P , сила лобового сопротивления R , линии действия которых проходят через центр масс М , а также нормальная реакция лыжни N с составляющими N ₁ и N ₂ и сила трения F _тр , приложенные к лыжам в точке M_L (рис.1):

P = mg , R = 0,5р ц V ², F mp = fN , N = N . + N 2 ,

где m – масса системы лыжник–лыжи, ρ – плотность воздуха, ? – аэродинамический параметр, найденный ранее экспериментально [5]. В работе [4] было принято допущение, что сила трения лыж о снег на поворотах существенно возрастает из-за врезания кантов лыж в снег, и коэффициент трения f линейно зависит от тангенса угла наклона лыжника к нормали к поверхности:

f = 0,05 + K tg(_Y),

где K – коэффициент пропорциональности.

Так как линия действия силы трения F _тр не проходит через центр масс, то в соответствии с принципом Даламбера лыжник должен немного отклониться назад, чтобы момент нормальной реакции N лыжни относительно материальной точки уравновесил момент силы трения. Дифференциальные уравнения движения центра масс по его траектории будут такими же, как и в работе [4]:

Здесь:

dV m — = mg sin a cos ф dt

- 2 рц V² — f4NW .

ds = V .

dt

N i =

—

mV ² cos² ф --+ mg cos a >  0,

R c

V ²

N2 = m--+ mg sin asm ф, rC

где φ – угол между направлением касательной к траектории центра масс и линией наибольшего ската склона горы.

Начальные условия движения:

при t = 0: s = 0, V = V ).

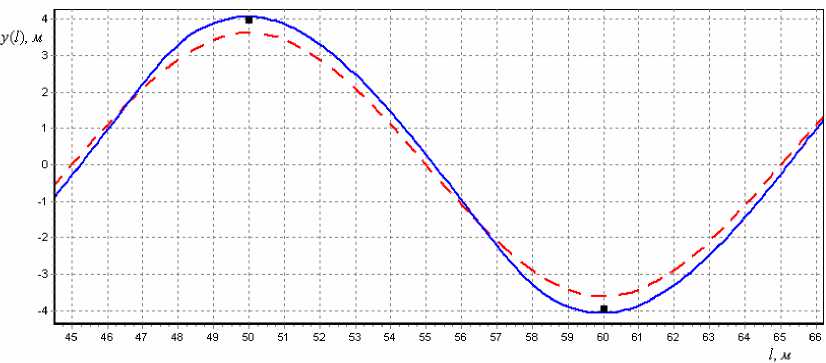
Рис. 2. Графики траектории центра масс (пунктирная линия) и траектории скольжения лыж (сплошная линия); квадратными метками изображены шесты; представлен третий период трассы

Решение задачи Коши (6) – (7) отличается от решения такой же системы уравнений в работе [4] тем, что в случае новой модели горнолыжника интегрирование уравнений (6) – (7) ведется по траектории движения центра масс, отличной от траектории в работе [4].

Результаты оптимизации слаломной траектории

Рассматривалось прохождение лыжником слаломной трассы на учебной базе Чайковского института физической культуры. Горнолыжный склон предполагался цилиндрическим с радиусом кривизны R_c = 520 м и начальным углом склона а₀ = 32 o . Параметры трассы: длина вдоль линии наибольшего ската 175 м, период слаломной траектории L = 20 м и отклонение шестов от средней линии наибольшего ската a = 4 м. Аэродинамический параметр ц принимался равным 0,48 [5]. Расстояние от центра масс системы до лыж усреднялось и было принято равным h = 0,5 м, коэффициент пропорциональности в формуле определения коэффициента трения (5) K = 0,24. Начальная скорость V ₀ равна той скорости, которую лыжник приобретает после прохождения 5 м по линии наибольшего ската от точки старта. Масса лыжника и лыж m = 78,08 кг.

Задача Коши (6)–(7) решалась методом пошагового интегрирования. Варьируемые параметры задачи - угол входа в поворот ф C и радиус кривизны траектории центра масс b_C вблизи шеста. Время спуска минимизировалось методом правильного симплекса.

Оптимальное значение времени спуска t min = 36,61 с достигается при ф C = 48,19° и b_C = 2,33 м. Это на 2,95 c меньше, чем при предположении о движении центра масс системы по траектории лыж [4].

На рис. 2 показаны оптимальная траектории центра масс (пунктир) и траектория лыж (сплошная линия), которая получена смещением точек оптимальной траектории центра масс на расстояние h sin(γ). Квадратными метками указанны шесты, которые лыжник должен объехать. Получены следующие оптимальные параметры слаломной траектории: угол входа в поворот фл = 50,2o, радиус кривизны при обходе шеста bл = 2,78 м. Кроме того, нужно заметить, что когда центр масс лыжника пересекает среднюю линию наибольшего ската ( y = 0), отклонение траектории лыж от этой линии составляет 0,22 м.

Заключение

Исследовано движение горнолыжника по трассе специального слалома на криволинейном склоне горы. Принятая модель горнолыжника позволила учесть влияние наклона лыжника при обходе шеста на время прохождения трассы. По сравнению с работой [4], где наклон лыжника не учитывался, минимальное время прохождения трассы уменьшилось приблизительно на 8%. В настоящей работе не учитывалось изменение расстояния от центра масс системы лыжник–лыжи до лыж. По результатам данной работы видно, что увеличение этого расстояния при обходе шеста должно привести к еще большему сокращению времени спуска.