Оптимизация управляющих воздействий при электролитическом способе получения алюминия

Введение. Процедуры математической оптимизации применяются в управляющих системах для выбора наилучшего одного или нескольких воздействий из области их допустимых значений. Наилучшие воздействия понимаются, как позволяющие достигнуть минимума или максимума целевой функции, то есть при выборе наилучшего комплексного воздействия на процесс, необходимо рассматривать три составляющих:

• -   выбор конкретных воздействий и ограничения на них;

• -   метод оптимизации;

• -    целевая функция.

Существует огромное число методов оптимизации, начиная от простых методов – перебора, покоординатного спуска, переходя к методам средней сложности – градиентным, симплексным и заканчивая генетическими алгоритмами [1; 2]. Отметим, что в настоящем исследовании мы не приводим принятую научную классификацию методов, а говорим лишь о методах, которые могут быть применены к текущей задаче – оптимизации управляющих воздействий при электролитическом способе производства алюминия.

Технико-экономические показатели эффективности процесса электролиза – это расход электроэнергии на тонну полученного алюминия, удельный расход углерода и фторидов, а также выход по току [3–7]. Расходные коэффициенты, конечно, связаны с выходом по току – чем ближе количество фактически полученного металла к теоретически возможному, тем ниже расход сырья и энергии в условиях одинаковой конструкции и технологии, но могут быть и особенности, например, конструкция может иметь высокий выход по току при хороших МГД-показателях, но большой расход энергии в связи с повышенными теплопотерями.

Можно рассматривать такие цели для достижения как заданные температура расплава и криолитовое отношение (КО) – показатель химического состава электролита, полагая, что технологическим персоналом уже определена эффективность назначенных значений, и можно устанавливать целью оптимизации снижение среднеквадратичного отклонения КО и температуры электролита от этих целевых значений.

Исходя из вышесказанного, определены группы критериев, по которым возможно проведение оптимизации:

• -    СКО температуры электролита от заданного целевого значения;

• -    СКО КО от заданного целевого значения;

• -    достижение целевого значения технологического параметра на конец периода оптимизации;

• -    минимизация удельного расхода электроэнергии на производство алюминия;

• -    максимизация выхода по току.

Существует деление на многокритериальную и однокритериальную оптимизацию с различными методами поиска локального или глобального экстремума, но будем считать, что целевая функция составлена таким образом, что она имеет один минимум или максимум и включает в себе наши требования к технологическому процессу.

Описание выбранного метода оптимизации. Для поиска оптимальных воздействий был выбран градиентный метод оптимизации - метод Коши [8], в основе которого лежит формула:

x ⁽ k ^{+ 1)} = x ^{( k} ) - а -V f ( x ^{( k} ) ), (!)

где шаг спуска а- заданный положительный параметр. Направление спуска определяется компонентами вектора градиента V f ( x ^{( k} ) ). Формула (1) предполагает спуск в случае n-мерного вектора воздействий:

x ^{( k} ) = ( x k , x 2 ,...., x ₃ ^k ), (2) где x i ^k - различные управляющие воздействия, на каждом шаге спуска или при нахождении градиента. Градиент для случая трех переменных (в нашем случае трех воздействий) запишется следующим образом:

∂ f ∂ f ∂ f

V f ( x ) = г • —+ j - I k • — . (3) ∂ x ∂ x ∂ x

Метод обладает двумя недостатками: возникает необходимость выбора подходящего шага спуска, также методу свойственна медленная сходимость к точке минимума вследствие малости градиента в окрестности этой точки.

Главное преимущество метода в его устойчивости - при достаточно малой длине шага итерации обеспечивается выполнение неравенства f(x(k+1)) < f (x(k)). Имеется теорема о достаточных условиях сходимости метода с постоянным шагом [9]. С учетом этого свойства метод Коши позволяет существенно уменьшить значение целевой функции при движении из точек, расположенных на значительных расстояниях от точки минимума.

В нашем случае достоинство этого метода перекрывает его недостатки. Ранее была реализована оптимизационная модель на основе метода покоординатного спуска, эксплуатация которой выявила недостатки: невысокая скорость поиска и уход в локальный экстремум, кроме того, при возрастании количества воздействий скорость работы значительно замедляется, так как метод перебирает шаги отдельно по каждому воздействию, поэтому градиентный метод более предпочтителен.

Шаг выбран экспериментально по чувствительности целевой функции, а очень близкий подход к точке минимума и не нужен - точность вычислений не должна значительно превосходить точность измерений. Зачастую достаточно одного спуска (в направлении первоначального градиента), чтобы получить минимум целевой функции с удовлетворительной точностью.

Формула (1) предполагает, что градиент может быть рассчитан на каждом шаге спуска, но практически реализуется следующий способ - градиент рассчитывается на многомерном первоначальном кресте воздействий и далее осуществляется спуск в направлении рассчитанного вектора антиградиента до тех пор, пока оптимизируемый технологический параметр не достигнет цели, или пока СКО этого параметра от цели не перестанет уменьшаться. В первом случае осуществляется выход из процедуры, и оптимизация считается успешно законченной, во втором случае в последней точке спуска, где было минимальное СКО, строится новый крест по всем воздействиям и выполняется поиск нового градиента.

Управляющие воздействия, на основании которых можно выполнять процедуру оптимизации следующие:

• -    добавка фторида алюминия;

• -    заданное напряжение;

• -    ток серии;

• -   уровень металла;

• -   уровень электролита.

Три первых воздействия могут осуществляться АСУТП автоматически, уровни расплавов регулируются технологическим персоналом по заданью АСУТП.

Реализация метода в программном обеспечении «Виртуальный электролизер». «Виртуальный электролизер» (ВЭ) – физико-математическая модель, которая имитирует работу электролизера для производства алюминия и предназначена для изучения динамики процессов, протекающих в нем [10-13]. Предназначена эта программа для технологического персонала, чтобы адекватно оценивать реакцию электролизера на управляющие воздействия.

Реализация разработанной оптимизационной процедуры выполнена в программе «Виртуальный электролизер» для того, чтобы не навредить реальному объекту управления, оценить все переходные процессы технологических параметров при комплексных воздействиях и устранить все возможные недочеты перед внедрением этой модели в АСУТП.

На текущий момент в системе управления уже функционирует модуль «Стабилизации состава электролита» [14; 15], который включает в себя оптимизацию для управления

Криолитовым Отношением (КО), мы же хотим расширить функционал дополнительными управляющими воздействиями и параметрами для оптимизации, а также целевыми функциями.

Опишем практическую реализацию метода в ПО «Виртуальный электролизёр» по двум воздействиям – добавка AlF 3 и заданное напряжение, расчет остальных воздействий в программной реализации осуществляется аналогично.

На рис. 1 представлено меню начальных условий для расчета, которые запрашиваются из базы данных АСУТП по конкретному электролизеру. После всех расчетов рекомендации также будут преданы по этому же электролизеру на верхний уровень АСУТП.

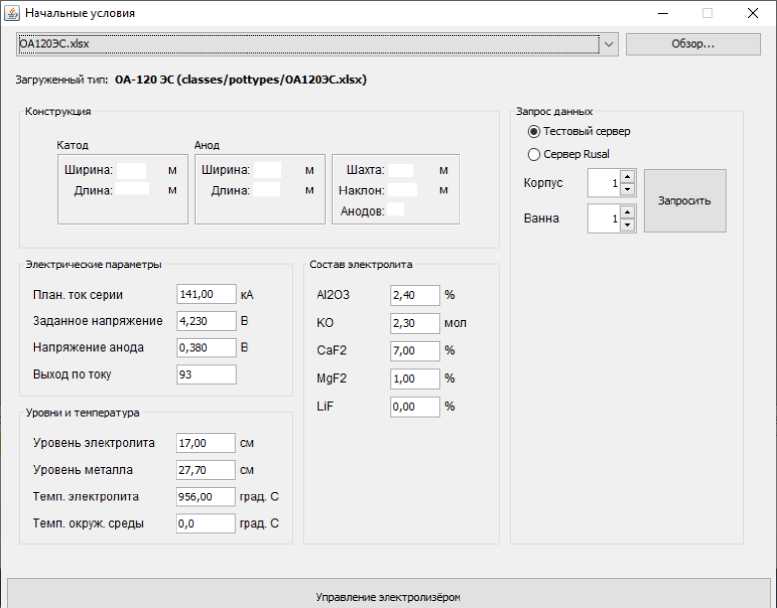
Рис. 1. Интерфейс начальных условий

Fig. 1. Initial conditions interface

В интерфейсе оптимизации (рис. 2) существует выбор между двумя методами – «Покоординатный метод» и «Градиентный метод». В качестве оптимизируемого параметра выбрана температура электролита. Начальная величина управляющих воздействий по добавкам фтора и напряжения, как и критерий завершения оптимизации также задаются пользователем в интерфейсе. В данном случае выбраны следующие добавки: 5 кг AlF 3 и 50 мВ уставка заданного напряжения, а также критерий выхода из оптимизации – достижение минимума СКО температуры от цели соответственно.

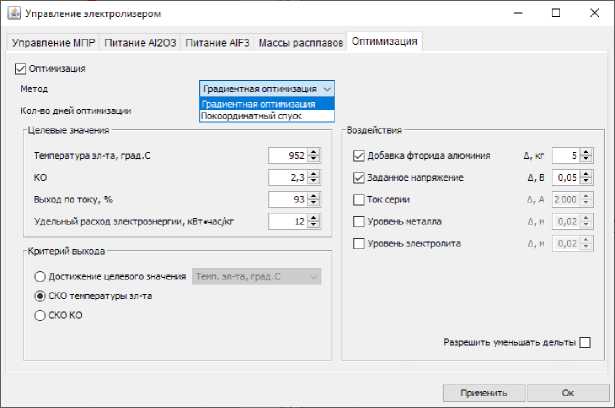
Рис. 2. Интерфейс оптимизации в ПО «Виртуальный электролизёр»

• Fig.2.    Optimization interface in the Virtual cell software

Расчет начинается с построения креста (рис. 3), на вершинах которого находятся выбранные воздействия с заданной величиной. В процессе спуска шаги по направлениям будут меняться, но крест всегда считается с изначально заданными добавками. Далее рассчитывается среднеквадратичное отклонение температуры электролита от цели (СКО Т) в четырех точках креста, а также в его середине.

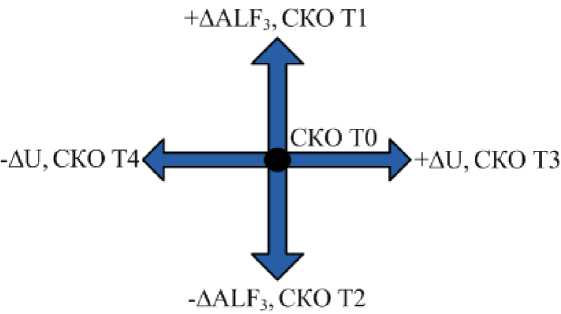
Рис. 3. Крест воздействий для оптимизации

• Fig. 3.    Cross impacts for optimization

Далее численно (методом конечных разностей) рассчитываем градиент, состоящий из частных производных:

DIF _ AlF = (СКО(Т 1 )-СКО(Т2)) / (2 -A A IF ),                     (4)

DIF _ U = (СКО(Т3)-СКО(Т4)) / (2 - A U) .                        (5)

Делаем проверку отличия градиента от нуля с заданной точностью. Длина вектора должна отличаться от нуля

Modgrad = V ( DIF _AlF ) ² + ( DIF_U ) ² .

Если не ноль, рассчитываем направление спуска к минимуму во внутреннем цикле, иначе выход из оптимизации. Внутренний цикл:

AAAlFk = AAAIF-1 - step - DIF _ AlF - AAIF ,(6)

AA Uk = AAUk-1 - step - DIF _ U - A U .(7)

ΔΔAlF 3 , ΔΔU – это шаги внутреннего спуска, на первом шаге спуска они равны ΔAlF 3 и ΔU, или нулю, потом пересчитываются. Дельты воздействий, найденные по формулам (6)-(7), добавляем к текущем значениям добавки сырья и напряжению,

AlFk = AlF0 + AAA lFk,(8)

Uk = U0 +AA Uk(9)

и считаем СКО Температуры, отрабатывая эти воздействия в течение установленных дней оптимизации в программе «Виртуальный электролизер». СКО Т должно уменьшаться и при первом расчете по формулам (8)-(9) оно должно быть меньше, чем СКО Т0. сравниваем с предыдущим значением в этом внутреннем цикле, должно выполняться

СКО( 7^k ) <  СКО( Г^{k - 1}).                                 (10)

Step зададим равным 1/Modgrad . В дальнейшем, при отладке для использования в алгоритмах АСУТП шаг по каждому воздействию может быть задан отдельно.

Выход из внутреннего цикла осуществляется двумя способами:

– СКО перестало уменьшаться – тогда нужно пойти на формулы (4)-(5) и пересчитать крест, градиент, и снова запустить внутренний цикл, но крест будет на новом месте, то есть в середине креста, точке Т0 теперь начальные значения AlF 3 ⁰ и U⁰ присвоятся последним, найденным по формулам (8)–(9);

– отклонение Температуры от целевого значения составило заданную точность, например, меньше 0,5 градуса, тогда оптимизация завершается.

Должен быть выход из процедуры оптимизации по зацикливанию – сравниваются СКО в серединах последних крестов, или три последних СКО в спуске – если они равны, то необходимо выйти из оптимизации и остановиться на последнем расчете воздействий. Зацикливание связано с тем, что процедура при выборе воздействий достигает ограничений, на них наложенных, например, добавка фторида алюминия не может быть меньше нуля, а для повышения расчетного КО это требуется.

Визуализация работы блока оптимизации в программе «Виртуальный электролизер». При активации оптимизации по умолчанию включается новый реализованный метод – метод градиентов (рис. 4) и в интефейсном окне отображения результатов становится доступной вкладка «Оптимизация» с двумя графиками.

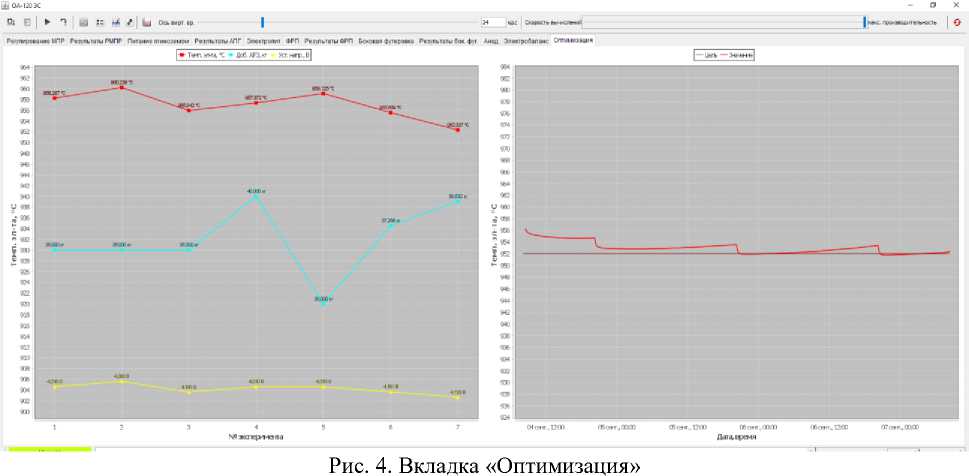
Fig. 4. Optimization tab

На левом графике отрисовывается «ход» оптимизации: выводятся величины воздействий и достигнутые значения оптимизируемого параметра для каждого эксперимента. На нём можно наблюдать в какую сторону «движется» оптимизация, рассчитывая величины воздействий для достижения целевого значения оптимизируемого параметра.

Например, согласно рис. 2, был выбран оптимизируемый параметр – температура электролита (цель 952 ° С), а воздействия - Доб. AIF 3 и Уст. напр. В эксперименте № 1 (согласно рис. 4) значения воздействий были следующие: Доб. AlF 3 = 35 кг и Уст. напр. = 4,23 В, при этом оптимизируемый параметр (температура электролита) достиг значения 958 ° С; в эксперименте № 2 значения воздействий были: Доб. AIF 3 = 35 кг и Уст. напр. = 4,28 В, оптимизируемый параметр достиг значения 960 ° С и т.д. Расчет креста закончился на эксперименте 5 и эксперименты 6 и 7 – это были шаги в сторону спуска.

График отрисовывается и дополняется до тех пор, пока оптимизация не достигнет цели, при этом, в случае с градиентной оптимизацией, цель может быть достигнута, для примера, в эксперименте № 7, но оптимизация продолжится на ещё несколько шагов вперёд и если её показатели не будут улучшаться, все последующие эксперименты после 7-го будут удалены с графика и на последнем эксперименте № 7 будут видны оптимальные значения параметров для достижения цели.

На правом графике отображается переходный процесс оптимизируемого параметра (рис. 4). График перерисовывается на каждом эксперименте и в конце оптимизации на него выводится переходный процесс, соответствующий эксперименту при котором была достигнута цель оптимизации. Детально можно посмотреть значение графика в любой временной точке виртуального времени, наведя курсор мыши на нужное место.

Все последующие тесты выполняются при начальных условиях, обозначенных на рисунках 5-7, меняются цели и параметры оптимизации. В следующем тесте № 2 выполним оптимальное повышение температуры электролита только за счет добавки AlF 3 – на рис. 5 представлены условия оптимизации.

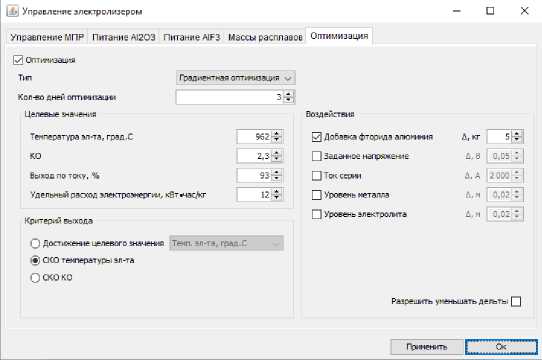
Рис. 5. Условия оптимизации в тесте № 2

Fig. 5. Optimization conditions in the test No. 2

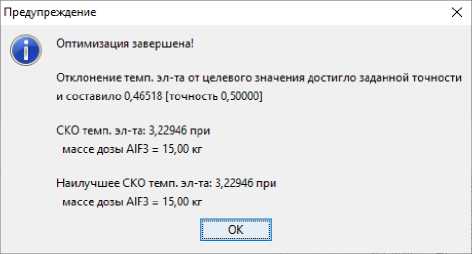
Рис. 6. Результаты оптимизации по тесту № 2

Fig. 6. Optimization results for the test No. 2

На рис. 6 и 7 представлен выбор снижения суточной добавки AlF 3 от 35 до 15 кг для повышения температуры электролита от 956 до 962 градусов. Здесь в отличие от теста № 1, суточное потребление и суточная добавка в начале расчета была равна 35 кг. На левом графике рис. 4 в экспериментах 1–2 алгоритм определялся, куда ему пойти, и далее за 3 шага спуска мы достигли заданной температуры.

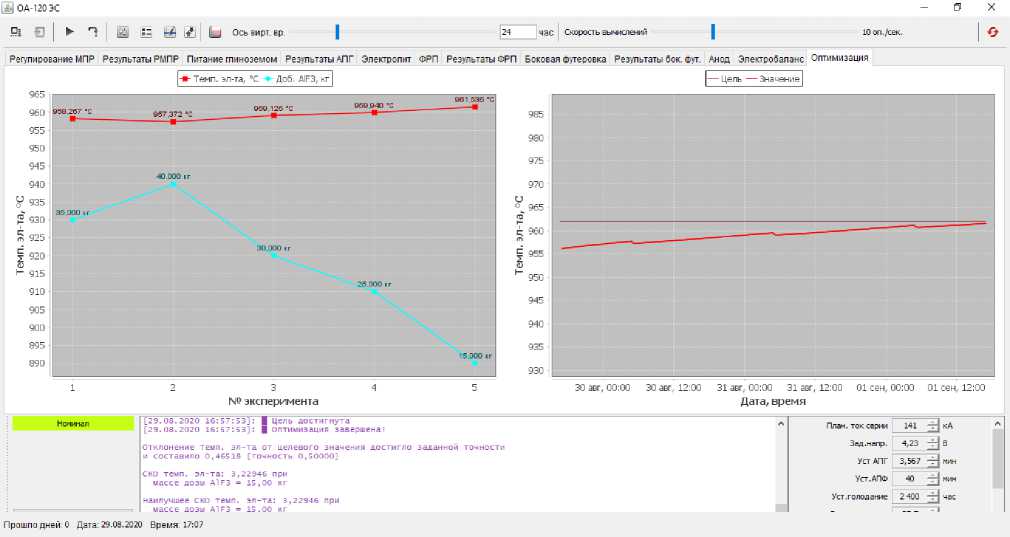
Рис. 7. Визуализация процедуры оптимизации при расчете № 2

• Fig. 7.    Optimization procedure visualization in the calculation No. 2

Тест №3 представляет оптимизацию при трех управляющих воздействиях. На рис. 8 представлены выбранные воздействия для снижения температуры электролита от 956 до 950 градусов. В отличие от теста № 1 программа здесь меньше увеличила дозу фторида алюминия, больше снизила напряжение и подняла высоту металла на 4 см, что видно в выводе результатов на рис. 9. На рис. 10 семь первых расчетов (экспериментов) составили трехмерный крест, затем до точки 11 осуществлялся спуск, далее программа начала строить новый крест, и в одной из точек нового креста достигла заданной точности.

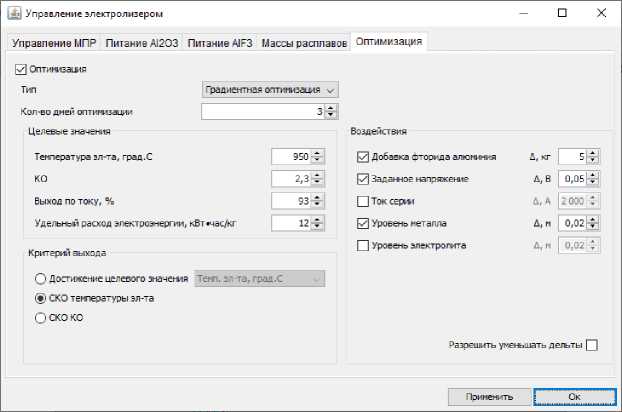
Рис. 8. Условия оптимизации в тесте № 3

• Fig. 8.    Optimization conditions in the test No. 3

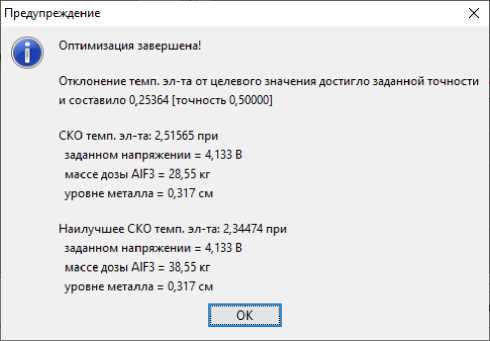
Рис. 9. Результат оптимизации при трех управляющих воздействиях

• Fig. 9.    Optimization result for three control actions

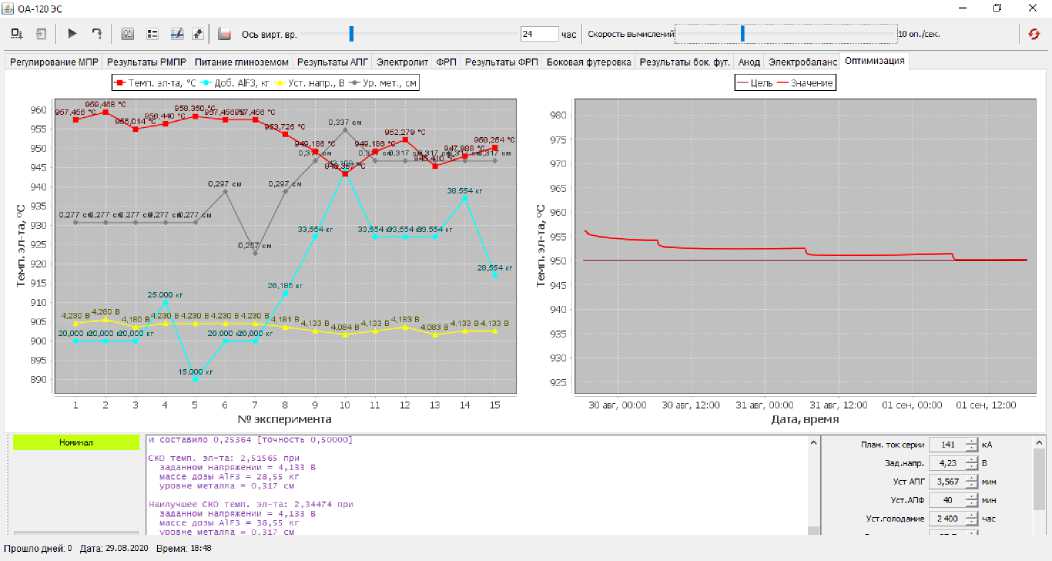
Рис. 10. Интерфейс результатов оптимизации при трех воздействиях, тест № 3

Fig. 10. Interface of optimization results with three influences, test No. 3

Заключение. В текущем исследовании был разработан, программно реализован и протестирован новый алгоритм расчета комплексного управляющего воздействия методом градиентного спуска для улучшения быстродействия и точности расчетов в ПО «Виртуальный электролизер». Разработан интерфейс для визуализации работы блока оптимизации и его настроек. Ход оптимизационных расчетов виден пользователю, как и поведение оптимизируемого параметра.

Разработанная оптимизации модель при её внедрении в систему управления позволит повысить качество управления технологическим процессом производства алюминия электролитическим способом, снизить удельный расход электроэнергии и снизить количество электролизёров с нарушенным технологическим режимом работы. Группа описанных целевых функций добавляет вариативность в возможных способах оптимизации тех или иных технологических параметров, но для практического использования в алгоритмах АСУТП важнее достижение целевого параметра и при внедрении это будет учтено.