Оптимизация условий ферментативной модификации пюре сахарной свеклы с использованием экспериментально-статистического подхода

В настоящее время перед хлебопекарной и кондитерской промышленностью стоит задача по созданию принципиально новых кондитерских и хлебопекарных изделий функционального назначения длительного срока хранения с целью экономии дефицитного сырья, совершенствования структуры ассортимента и снижения сахароемкости. Использование местных нетрадиционных видов растительного сырья может способствовать решению поставленной задачи.

Сахарная свекла – техническая культура с большим потенциалом применения в пищевой промышленности, использование которой в настоящее вр емя недостаточно. Биохимический потенциал сахарной свеклы обусловливает широкие возможности ее применения в пищевой промышленности с целью повышения пищевой и биологической ценности продуктов питания. В связи с этим, актуальной является создание новой схемы переработки сахарной свеклы в полуфабрикат, который представляет собой концентрированную пасту с массовой долей сухих веществ 40-60 %.

Концентрированная паста из сахарной свеклы может стать альтернативой основному сырью кондитерского производства - сахару и патоке, выполняя структурообразующую роль

Магомедов М.Г., Литвинова А.А., 2013

в кондитерских изделиях и повышая их пищевую ценность, сокращая при этом технологический процесс и значительно снижая себестоимость готовой продукции.

Качество концентрированной пасты зависит от вязкости используемого пюре, резкое возрастание которой при концентрировании замедляет процесс удаления влаги, усложняет работу оборудования, а также приводит к снижению органолептических и физикохимических показателей готовой продукции.

Как известно, вязко-пластичные свойства фруктового и овощного пюре обусловлены содержанием пектиновых веществ (протопектин, растворимый пектин, пектин межклеточного вещества), гемицеллюлоз и целлюлоз.

Для обеспечения равномерного протекания процесса концентрирования свекловичное пюре подвергали ферментативной обработке, использовали ферментный препарат нового поколения Rohapect DA6L (производитель – фирма AB Enzymes GmbH, Германия), который представляет собой высококонцентрированный комбинированный пектиназнo-aрабаназный ферментный препарат, полученный в результате ферментации штамма Aspergillus niger.

Приготовление свекловичного пюре и его дальнейшая переработка сопровождается механическими, теплообменными и массообменными процессами: перемешиванием, транспортированием по трубопроводу, дозированием. При реализации указанных процессов происходит изменение структуры пюре, в результате чего его реологические св ойства претерпевают значительные изменения, которые могут существенно влиять не только на качество готового изделия, но и на работу оборудования и его энергозатраты.

Кроме того, вопросы интенсификации, автоматизации и оптимизации процесса производства пюре не могут успешно решаться без знаний реологических свойств полуфабриката и закономерностей его реологического поведения.

Для оптимизации условий ферментативной модификации свекловичного пюре был применен экспериментально-статистический подход [2].

В качестве основных факторов выбраны (таблица 1): х i - дозировка ферментного препарата, % к массе пюре; х ₂ - температура ферментации, ° С. Выходным параметром у служила эффективная вязкость свекловичной массы, Па-с. Выбранные факторы совместимы и не коррелируют между собой. Вискози-метрические исследования проводили на вибровискозиметре SV-10.

Таблица 1

Характеристики планирования

Условия планирования	Дозировка ферментного препарата х 1 , %	Температура ферментации x 2, °С
Основной уровень (0)	0,06	65,90
Интервал варьирования	0,03	10,00
Верхний уровень (+1)	0,09	75,90
Нижний уровень (-1)	0,03	55,90
Верхняя «звездная» точка (+1,41)	0,10	80,00
Нижняя «звездная» точка (-1,41)	0,05	55,00

Первый этап заключался в построении регрессионного уравнения, адекватно описывающего зависимость выбранного выходного параметра от изучаемых факторов. Для этого был реализован активный эксперимент по системе центрального композиционного униформ-ротатабельного плана, обеспечивающего полу чение одинаковой величины дисперсии выходного параметра для любой точки в пределах изучаемой области. В результате статистической обработки экспериментальных данных получено уравнение регрессии (1), адекватно описывающее зависимость эффективной вязкости свекловичного пюре у отисследуемых факторов:

у = 5,83 + 0,26 X 1 + 0,72 X ₂ - 0,2 X 1 X ₂ + 0,03 X ² - 0,23 X ₂ ²,           (1)

где X i - кодированные значения факторов, связанные с натуральными значениями x i соотношениями (2):

X 1 =

х 1 - 0,06_; 0,03 ’

_ x 2 - 65,9

X 2 =   77

Второй этап заключался в геометрической интерпретации и анализе регрессионного уравнения. Графические интерпретации уравнения (1) в виде поверхности отклика и двумерных сечений представлены на рисунках 1, 2.

Анализ графических зависимостей (рисунки 1, 2) и уравнения регрессии (1) показал, что чувствительность эффективной вязкости свекловичного пюре к изменению температуры ферментации в несколько раз превышает аналогичную чувствительность к изменению дозировки ферментного препарата.

Из этого следует важный вывод: при практической реализации указанных режимов приготовления свекловичного пюре следует обеспечить строгое поддержание температуры ферментации на заданном значении, избегая ее значительных колебаний, которые могут привести к получению пюре с неудовлетворительными реологическими свойствами. К постоянству дозировки ферментного препарата, в свою очередь, могут быть предъявлены менее жесткие требования.

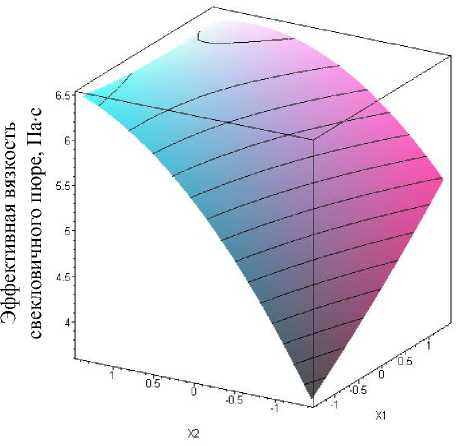
Рисунок 1 - Зависимость эффективной вязкости свекловичного пюре от дозировки ферментного препарата X 1 и температуры ферментации X 2

Дозировка ферментного препарата

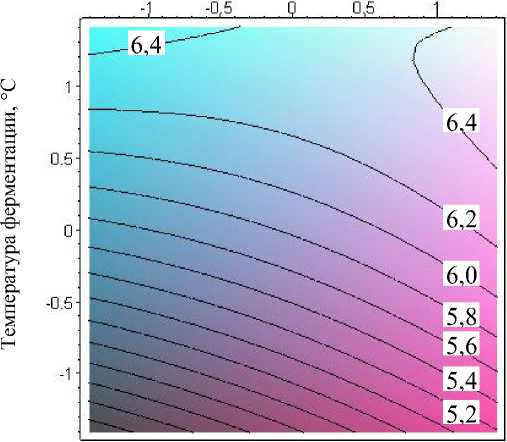
Рисунок 2 - Линии равного уровня эффективной вязкости свекловичного пюре (числа на кривых – значения эффективной вязкости, Па - с)

Третий этап заключался в поиске оптимальных режимов ферментативного гидролиза свекловичного пюре.

Задача оптимизации при этом была сформулирована следующим образом : необходимо найти такие значения независимых переменных Х1 и Х2, при которых эффективная вязкость свекловичного пюре y достигает мини- мального значения. При этом независимые переменные Х1 и Х2 должны находиться в области эксперимента, границы которой определяются значениями факторов в «звездных» точках, т. е. - 1,41 < X. < +1,41 .

Для этого запишем условие оптимизации в виде:

в котором последнее уравнение определяет границы области эксперимента (сфера радиу-coм R ) и является ограничением на значения независимых переменных.

Для решения поставленной задачи воспользуемся методом неопределенных множителей Лагранжа. Для этого составим целевую функцию F вида:

F = 5,83 + 0,26 Х 1 + 0,72 Х ₂ - 0,2 Х 1 Х ₂ + 0,03 Х 1² - 0,23 Х ₂ ² + х ( X 1² + X ₂ ² + X 2 - R ² ), (4) где X — неопределенный множитель Лагранжа.

В соответствии с вычислительным алгоритмом метода неопределенных множителей Лагранжа составим систему уравнений:

— = 0,26 - 0,2 X, + 0,06 Х . + 2 x X = 0;

dX ,       211

— = 0,72 - 0,2 X. - 0,46 X, + 2 X X, = 0;

дX 2                   1,2

— = X ² + X 2 - R ² = 0.

[дЛ

Для решения системы уравнений (5) с последующим вычислением значений функции отклика y воспользуемся интегрирован- ным пакетом MAPLEW 10. Вычисления проводим при изменении радиуса сферы R в диапазоне от 0 до 1,5 (таблица 2).

Таблица 2

Поиск оптимальных параметров

№ шага	R	X 1	X 2	X	у , Па - с
1	0	0	0	2,913	5,830
2	0,2	-0,067	-0,188	2,177	5,666
3	0,4	-0,134	-0,377	1,221	5,480
4	0,6	-0,2	-0,566	0,902	5,276
5	0,8	-0,266	-0,754	0,742	5,049
6	1,0	-0,331	-0,943	0,646	4,800
7	1,2	-0,397	-1,132	0,583	4,531
8	1,4	-0,460	-1,321	0,537	4,240
9	1,41	-0,465	-1,331	0,535	4,225
10	1,6	-0,527	-1,51	0,503	3,929

Как видно из результатов оптимизации (таблица 2), движение по поверхности отклика от центра к ее периферии сопровождается постепенным уменьшением параметра оптимизации y . Однако оптимальными следует признать условия, полученные на 9 шаге оптимизации, так как в этом случае независимые переменные Х 1 и Х 2 не выходят за границы области эксперимента, а эффективная вязкость свекловичной массы принимает минимальное значение.

Переходя от кодированных значений факторов к натуральным с учетом условий планирования (таблица 1), получим оптимальные значения факторов и параметра оптимизации: дозировка ферментного препарата x1 = 0,046 % к массе пюре; температура фер- ментации х2 = 52,59 °С; эффективная вязкость свекловичного пюре у = 4,225 Па-с.

Четвертый этап заключался в экспери -ментальной проверке оптимальных параметров и оценке степени точности и надежности полученного значения параметра оптимизации.

При оптимальных значениях дозировки ферментного препарата x 1 = 0,046 % к массе пюре и температуре ферментации х ₂ = 52,59 ° С были изготовлены образцы свекловичного пюре ( n = 10 шт.), в которых определяли эффективную вязкость. В таблице 3 представлены средние арифметические значения эффективной вязкости y^э и дисперсии S ², полученные по результатам десяти параллельных опытов.

Как видно из таблицы 3, расчетное и экспериментальное значения эффективной вязкости несколько отличаются друг от друга. Для того, чтобы эти различия признать несущественными и объяснить только случайной ошибкой, была выдвинута нуль-гипотеза о том, что расчетное и экспериментальное значения параметра оптимизации принадлежат к одной и той же генеральной совокупности.

Таблица 3

Результаты оптимизации

Значение эффективной вязкости свекловичного пюре, Па ⋅ с		Дисперсия S 2	Расчетное значение критерия Стьюдента t р	Ошибка δ , Па ⋅ с	Доверительный интервал эффективной вязкости свекловичного пюре, Па ⋅ с
Расчетное yр	Экспериментальное yэ
4,225	3,988	0,144	1,98	0,274	3,951 ÷ 4,499

Для проверки выдвинутой нуль-гипотезы воспользуемся распределением Стьюдента. При этом вычисляем расчетное значение критерия Стьюдента (таблица 3):

t р

y^э - y^р

S ²

n

Сравнение величины t р с табличным значением критерия Стьюдента t т = 2,29 (при числе степеней свободы f = 9 и принятой доверительной вероятности γ = 95 %) показывает выполнение условия t _р < t _т . Это указывает на то, что выдвинутая нуль-гипотеза может быть принята, т. е. различия между расчетным и экспериментальным значениями эффективной вязкости свекловичного пюре следует признать несущественным (с доверительной вероятностью 95 %) и объяснить только случайной ошибкой. Ошибка предсказания значения параметра оптимизации (таблица 3):

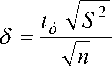
Результаты вычислений представлены в таблице 3 в виде доверительного интервала y^ð ± δ при принятой доверительной вероятности γ = 95 %.

Как видно из результатов таблицы 3, значение эффективной вязкости свекловичного пюре не выходит за границы доверительного интервала, полученного расчетным путем, что указывает на достоверность и надежность полученных результатов.