Оптимизация в моделях однокогортной популяции с учетом сохранения ее потомства

Теорема 1. При выполнении условий (6) оптимальное одноимпульс ное управление имеет вид[5]

Re'mM(/-/0)

где /д находится из условия г;^|/?£х'К"с/'=е}-

Доказательство. Гамильтониан задачи (11)-(14) выглядит как

= e~^r'w(l)v(t)- ц/_х (tXmx^t) + ХО) + +y₂(t)b(.t)x(t).

Отсюда имеем следующую сопряженную систему

X (?) = т^, (/) - 5(0^_: (0,         (15)

^(0 = 0           (16)

с граничными условиями ^(П^0,уХГ)>0,

^,(ПХП + ^(П(ЯП-0 = О.

Нетрудно видеть, что функции ХХх^Х^ХО не имеют разрывов в точках импульсов, и поэтому из (16) следует, что у/,(/) = const = \уг > 0.

Из непрерывности 6(0 и уравнения (15) следует гладкость функции ^(г). Кроме того, будем предполагать, что в задаче (11)-(14) существует оптимальное решение с импульсом в одной точке t₆<6<Т, т.е.

и(Г) = с50-в) + и(Д       (17)

В силу принципа максимума[2] выполняется соотношение

Ни (0 ^ -^ (0 + е"" X') £ 0 о о^Мге^'и-С/Х^У),        (18)

Из этих соотношений и гладкости функции ^(0 ^и унимодальности функции e'^wQ) следует, что эти функции касаются в одной точке 0, причем при 1*6 неравенство (18) будет строгим, следовательно, м(/) = 0 для 1*6 в левой части формулы (17). Отсюда также следует, что с = Ке"”^й. Допустим, что ул=0. Тогда ^ (0 = Х(°>" = wCSK'^e"” и e~ⁿw(0 касаются в единственной точке 9 = 1^. Следовательно, x(t) = 0 для t>t* и поэтому в силу первого неравенства (6)

R^b^X^dt = £ b(t)xV)dt < Q, что противоречит условию (10) задачи (7)-(10). И так ^2>0, следовательно, ХЛ = 2 в силу второго граничного усло вия.

Напишем условие касания функции ^(г) и е""Х0 в точке 6

^(6) = e'r6w(6),

< ^х(0) = т^х(0)-^2Ь{0)^

e"re (w(6) - rw(9)).

Из первого равенства и первого уравнения сопряжённой системы (15) получим

4-£^,6(т)е ^'бт - £<д₂6(т)е "Хт).

Подставив эту формулу во второе уравнение, окончательно получаем

ХУ) bi&^₂e^re r + m —~ =   —

Х^)   Х^)

Это уравнение имеет решение 0>С, так как 6(0) > 0 (если бы Ь<в\ = О, то 6(0 = 0 V/ <  9 ). Так как х^ = О V/ е [^Г] и у(Л = 6, то

R^tXr*dt = Q.

Наименьшее значение t^ - min 0, которое удовлетворяет этому уравнению, будет точкой импульса. Из (19) можно определить ^₂ и функцию ^(0- Теорема доказана.

2. Модель Кларка с ограничением

Модель Кларка [1] с ограничением имеет следующий вид

£* е'" (w(z)x(Ou(O - CuV))dt -> max, (20)

£6(OWr-e>0,  (21)

x(0 = Цт + и(О)х(/),    (22)

x(0) = R, w(/)>0.

Теорема 2. При ^ b^x'^dt^Q оптимальный процесс в задаче (20Н22) будет как в классической модели Кларка [3,5], а в противном случае оптимальная численность x(z) и оптимальное управление w(z) выражаются соответственно формулами

Re’^w, Osr <<,

Cr

*V) = '

w^tXm + r ~^) - Шпе^л w(O

<

x(t‘IKm,,                  ^<1,

0 d^AA,

/e[z*Z2],

где t*,t₂ и неопределенный множитель

Л > 0 определяются из системы

- Re""1 - (-ти^Г,') + ^(Z,*) + Я6(/* )ert' ) M’tORe^'-C

-Л-е"1 b(t*2) = mwV2)- w(Z2), p№(O^ = 0.

пряженное уравнение для задачи (20)-(22) имеют виды

H(x(z),^(z),u(z),A) =

= e'iT^(x(Z),g(Z),w(Z),^) =

= e"rl(w(t)x(t)u(f) -Си(<) + AbV)xU>n --q(Z)(m + и(ГМ0Х

q(l) = ~w(i)u(t) - Ab(t)eri +

+qUXm+u(t)) + rq(O-

Из условия оптимальности мы получаем [4] ан

—~ = w(z)x(/) - С - qUW) = 0 =>ди

w(t)x{t) + w(Z)£(Z) - q^x^t) - qVW) = 0.

При x(t)^O мы для оптимальной численности во время вылова имеем

ДО =-----------■ (23)

w(rXm + г - — J) - XbW" и<0

Оптимальное время t* начала рыболовства определяется из формулы (23) при условиях x(t’) = -тх(Д), x(t*) = R • e""’ :

H<)Re’4-C

Из условия Л > 0, мы видим, что момент начала вылова t* не меньше чем начальный момент вылова z, в классической модели Кларка [3]. Вылов должен завершиться в тот момент, когда значение подынтегральной функции становится отрицательным, т.е. время завершения вылова Z* определяется равенством

Л ■e^r,'‘b(t₂) = mw^)- й’(г’),    (25)

что означает (/, 2), где z2- время завершения вылова в классической модели Кларка [3]. Пусть х*(0 оптимальная численность в классической модели Кларка, которая выражается формулой г

Re"m', Cr ir(Z)(r + /«- -^2) w(Z)

x4kX”\

0

Доказательство. Гамильтониан и со

Ясно, что при Г Ь^)х* (t)dt > Q будут

Z* =z_pZ* =Z₂, и*(Z) = «(О,

V(Z) = x(Z), Л = О, где z/(Z), u(z) - соответственно оптимальные управления в классической задаче Кларка и в нашей задаче, х\г), х(О - соответствующие численности популяции.

В случае ^b(t)x*(0dt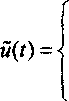 неопределенный множитель Л и моменты времени z’(A), z₂(A) определяются из соотношений (24)-(25) и дополнительного уравнения £ b(0x(0dt = Q, где х^ =

Rew,                0

Cr

= 1----------------------’ tx ~1-^'