Оптимизационное моделирование и алгоритмизация управления процессом дезагрегации ресурсов и объемов деятельности в структурно сложной системе с цифровым трансфером решений
Автор: Гусев Павел Юрьевич, Львович Яков Евсеевич
Рубрика: Управление сложными системами
Статья в выпуске: 1, 2024 года.
Бесплатный доступ
Статья посвящена разработке оптимизационных моделей и алгоритмов управления процессом дезагрегации ресурсов и объемов деятельности в цифровизированной системе, под которой понимается структурно сложная система, где взаимодействие управляющей и деятельностной сред осуществляется посредством цифрового трансфера принимаемых решений. При этом структура такой системы характеризуется многослойно-распределительной топологией, а процесс дезагрегации представляет собой процесс разделения заданного уровня ресурсов и объема деятельности. Рассмотрена процедура формирования оптимизационной модели процесса дезагрегации по видам ресурсов. Предварительно проводится экспертное оценивание потребностей и коэффициентов значимости ресурсов. С ориентацией на требования управляющей среды и экспертные оценки определены альтернативные варианты дезагрегации. Выбор лучшего варианта распределения заданного уровня по видам ресурсов и оптимального решения для цифрового трансфера в деятельностную среду осуществляется на основе оптимизационной модели линейного программирования. Алгоритмизация принятия решения базируется на двух этапах: переход к двойственной задаче линейного программирования и сравнительный анализ альтернативных вариантов по значениям целевой функции этой задачи, получение решения прямой задачи линейного программирования с учетом выбранного варианта распределения по видам ресурсов для последующего цифрового трансфера. Сформирована оптимизационная модель процесса дезагрегации объема деятельности, позволяющая на основе решения задачи линейного программирования принять решения для последующего цифрового трансфера в деятельностную среду.
Цифровизированная система, процесс дезагрегации, управление, экспертное оценивание, оптимизация
Короткий адрес: https://sciup.org/148328219
IDR: 148328219 | УДК: 681.3 | DOI: 10.18137/RNU.V9187.24.01.P.11
Текст научной статьи Оптимизационное моделирование и алгоритмизация управления процессом дезагрегации ресурсов и объемов деятельности в структурно сложной системе с цифровым трансфером решений
Эффективность принятия решений при управлении сложной системой существенным образом зависит от ее структуры, топология которой определяется характером объединения экспертов в организационное целое посредством различного рода связей [1]. Традиционно рассматриваются следующие топологии связанности элементов [2]: линейные, централистские, сетевые, сотовые, скелетные, полносвязные. Особый класс составляют структурно сложные системы [3].
К этому классу следует отнести современные системы, возникающие на базе цифровых платформ в разнообразных сферах деятельности [4]. Такие системы будем называть цифровизированными , относя к ним сложные системы, в которых взаимодействие управляющей и деятельностной сред осуществляется при помощи цифрового трансфера принимаемых решений. В работе [5] показано, что в отличие от традиционных систем структура цифровизированной системы имеет многослойно-распределенную топологию.
В первом слое – управляющей среде – задаются граничные требования для последующей дезагрегации интегрального уровня ресурсов V 0 и объема деятельности X 0 . Второй слой – ресурсная среда – связан с распределением интегрального V 0 по n = 1, N видам
Оптимизационное моделирование и алгоритмизация управления процессом дезагрегации ...
ресурсов – Vn 0 . Третий слой – цифровая среда – является базовым в цифровизированной системе и обеспечивает трансфер решений по дезагрегации характеристик Vn 0 , n = 1, N и X 0 через i = 1, I цифровых сервисов в четвертый слой – деятельностную среду. С этой целью определяется следующая последовательность решений: распределение Vn 0 , n = 1, N и X 0 с привязкой к цифровым сервисам Vn i , i = 1, I , n = 1, N и X i , i = 1, I ; распределение Vn i , i = 1, I , n = 1, N и X i , i = 1, I по m = 1, M видам деятельности – Vm i n , i = 1, I , m = 1, M , n = 1, N и Xm i n , i = 1, I , m = 1, M , n = 1, N . Для формирования обратной связи с управляющей средой используется пятый слой – мониторинговая среда.
Распределительный характер топологии цифровизированной системы связан с процессом дезагрегации ресурсов и объемов деятельности. Под процессом дезагрегации будем понимать процесс разделения заданных объемов ресурсов и деятельности в цифровизированной системе в соответствии с уровнями многослойно-распределительной топологии. Результатом процесса являются альтернативные варианты разделения. Для выбора наилучшего варианта используется оптимизационный подход [6; 7].
В [5] оптимизационный подход использован для формирования многоуровневого комплекса задач управления процессом дезагрегации в цифровизированной системе. На уровнях, связанных с распределительными механизмами в ресурсной среде, и при реализации цифрового трансфера решений принятие решений осуществляется на основе оптимизационных моделей, которые формируются с использованием экспертной информации. Инвариантные методы такого подхода изложены в [8]. Требуется их проблемная ориентация на особенности исследуемого класса структурно сложных систем. Поэтому целью статьи является разработка оптимизационных моделей, ориентированных на принятие решений при управлении дезагрегацией ресурсов и объемов деятельности в цифровизированной сложной системе .
Для достижения указанной цели в статье решены следующие задачи:
-
• формирование оптимизационной модели и алгоритма принятия решения при управлении процессом дезагрегации по видам ресурсов с учетом цифрового трансфера решений в деятельностную среду;
-
• формирование оптимизационной модели дезагрегации объема деятельности для трансфера в деятельностную среду через множество цифровых сервисов.
Формирование оптимизационной модели и алгоритма принятия решения при управлении процессом дезагрегации по видам ресурсов
Как показано в [5], процесс дезагрегации по видам ресурсов осуществляется за счет следующих распределительных механизмов:
-
• распределение интегрального уровня ресурсов V 0 , определяемого управляющей средой, между n = 1, N видами ресурсов – Vn 0 , n = 1, N ;
-
• распределение ресурсов Vn 0 , n = 1, N между i = 1, I сервисами цифрового трансфера решений в деятельностную среду – Vn i , i = 1, I , n = 1, N .
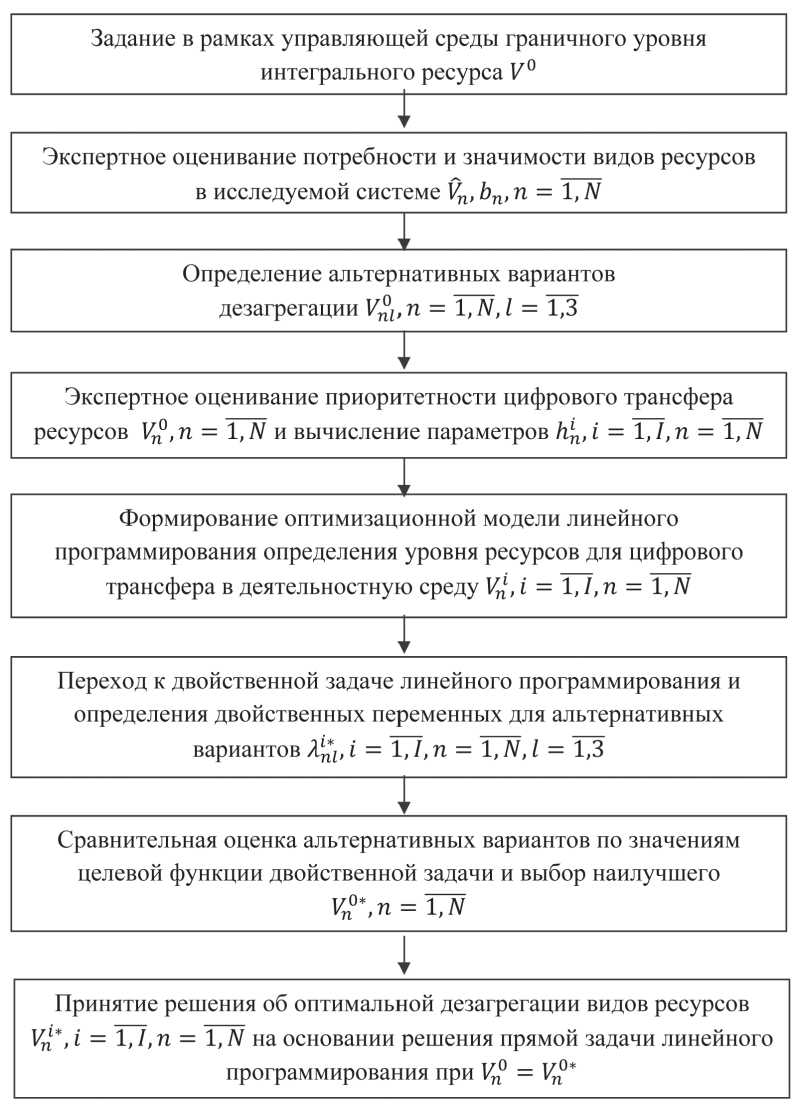
Оптимизационная модель объединяет оба механизма. В рамках первого механизма применяются экспертные оценки потребности и значимости каждого вида ресурса для последующей цифровой трансформации решений, принятых с использованием этих оце- нок. В [9] проводится способ привлечения экспертов для оценки потребностей V,, п = 1, N и коэффициентов значимости ресурсов: N bn,n = 1,N,0 n=1 Полученные данные позволяют получить альтернативные варианты распределения для разных реализаций первого механизма [9]. Пропорциональное распределение: 17 ° Vn 1 = 1 л b V и и EN л bnVˆn N V,,еслиУуп < V° n=1 N - V °, если У Vn > V °, n = 1N n n=1 n=1 Распределение по принципу обратных приоритетов: A П V — - g(1 -bn ) , n = 1, N, Параметрическое распределение: 00 n3 где g - параметр распределения, отвечающий условию N £V3 = V° «Р« V3 > °. Для оптимизации второго механизма распределения необходимо учесть альтернатив- ный характер вариантов Vn0 в соответствии с (2)–(4) и определить экспертные оценки приоритетности трансфера этого решения через i-й цифровой сервис как I hn,i = Ij,n = 1N,° При этом экспертное оценивание (5) осуществляется для каждого n-го вида ресурса по методике, изложенной в [9]. Соответственно, оптимизационные модели формируются тоже для каждого n-го вида ресурса. В качестве экстремального требования принимается максимальная значимость при влечения ресурсов при цифровом трансфере Vn°, п = 1, N в деятельностную среду: NI yyhnVn0 i ^ max; (6) n=i i=i граничные требования: • соответствие альтернативным вариантам распределения (2)–(4) Оптимизационное моделирование и алгоритмизация управления процессом дезагрегации ... I Уу0i< v^, n=1N, ,=13 i=1 • неотрицательность оптимизируемых переменных V„oi > 0, i = 1, I, n = 1, N. Объединив (6)–(8), получим оптимизационную модель линейного программирования с альтернативными значениями V°, n = 1, N, I = 1,3: NI J&0i ^ max, n=1 i =1 EVi< Vn0,n =1N,I = 13 (9) i=1 V0i > 0, i =Ц, n = 1N. Для сравнительного анализа и выбора наилучшего варианта альтернативных гранич- ных требований найдем оптимальное решение Х,,=1,I, n = 1,N, I = 1,3 двойственной к (9) задаче линейного программирования [10]: NI n=1 NN УХ >уп, i=й, n=1 xn > 0, i=1J, n=1N, I=13. Определение наилучшего варианта распределения (2)–(4) осуществляется путем вы- числения целевой функции задачи (10) и выбора Vn0 ,n = 1,N по условию ^ ,, = 1,3. Далее решается задача (9) при Vn0 = Vn0 и осуществляется трансфер полученного ре шения Vn , i = 1,I, n = 1,N для его дезагрегации по видам деятельности (см. Рисунок). Рисунок. Структурная схема оптимизационного моделирования и оптимизации управления процессом дезагрегации видов ресурсов Источник: схема составлена авторами. Оптимизация процесса дезагрегации объема деятельности для цифрового трансфера решений в деятельностную среду Дезагрегация объема деятельности основана на распределительном механизме, позволяющем распределить интегральный уровень X0, определенный управляющей средой между i=1,I, сервисами цифрового трансфера решений в деятельностную среду – Xi,i =1,I. Оптимизационное моделирование и алгоритмизация управления процессом дезагрегации ... Для формализации экстремального требования, связанного с трансфером решений X1, i = 1, I, в зависимости от приоритетности управления объемом деятельности через 1-й цифровой сервис используются экспертные оценки, аналогичные (1): I b1, 1 = 1j,0 < b1 <1,^b1 = 1. (12) 1=1 Оценки (12) позволяют в качестве целевой функции задачи оптимизации применять следующую: I Jp1 ^ max. (13) 1=1 Граничные требования при построении оптимизационной модели определяются следующими условиями: • непревышение интегрального уровня X I £X1 < X0; • сбалансированность цифрового iтрансфера решений по уровню ресурсов Vn , 1 = 1,1,n = 1, W и распределенного объема деятельности X1, 1 = 1,1 g^X1 < V*, 1 = 1j, n = 1N, где gn - удельная потребность в ресурсе Vn , 1 = 1,I, n = 1, W при получении объема деятельности X1, 1 = 1,I; • неотрицательность значений X1, 1 = 1,I X1 > 0,1 = й. Объединив экстремальное требование (13) и граничные требования (14)–(16), получим следующую оптимизационную модель: I ^b1X1 ^ max, i=1 I ^X1< X 0, (17) i=1 g^X1< V';, 1=1J, П=1W, x1 > о, 1=1,7. На основании решения задачи линейного программирования (17) [10] можно определить значения X1 , 1 = 1,1. Далее осуществляется трансфер полученного решения X1 для его дезагрегации по видам деятельности. Заключение Цифровизированная система является структурно сложной системой с многослойнораспределительной топологией, что приводит к необходимости многоуровневой оптимизации принятия решений при управлении процессом дезагрегации ресурсов и объемов деятельности. Оптимизационное моделирование и алгоритмизация принятия решений при управлении процессом дезагрегации по видам ресурсов базируется на экспертных решениях и решениях задач линейного программирования. Особенность заключается в необходимости учета альтернативности вариантов дезагрегации уровня ресурса, задаваемого управляющей средой при цифровом трансфере решений в деятельностную среду. Сравнительная оценка и выбор лучшего варианта осуществляются по значениям целевой функции при оптимальных значениях переменных двойственной задачи линейного программирования. При оптимизации процесса дезагрегации объема деятельности, задаваемого управляющей средой, учитываются приоритетность управления и сбалансированность с решением по распределению всех видов ресурсов посредством трансфера решений каждым цифровым сервисом. Оптимальный вариант дезагрегации определяется на основе решения задачи линейного программирования. Цифровой трансфер полученных оптимальных решений для видов ресурсов и объемов деятельности позволяет перейти к следующему уровню дезагрегации по видам деятельности.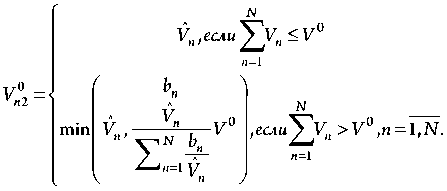
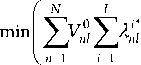
Список литературы Оптимизационное моделирование и алгоритмизация управления процессом дезагрегации ресурсов и объемов деятельности в структурно сложной системе с цифровым трансфером решений
- Нечипоренко В.И. Структурный анализ систем. М. : Советское радио. 1977. 216 с.
- Новосельцев В.И. Системный анализ: современные концепции. Воронеж : Кварта, 2003. 360 с. ISBN 5-89609-011-0.
- Мирзаахмедов М.К., Норматов Р.Н. Структурно сложные системы и вопросы их надежности // Universum: технические науки : электрон. науч. журн. 2023. № 1 (106). DOI: 10.32743/ UniTech.2023.106.1.14899.
- Гретченко А.И., Горохова И.В. Цифровая платформа: новая бизнес-модель в экономике России // Вестник Российского экономического университета имени Г.В. Плеханова. 2019. № 1 (103). С. 62-72. EDN VVACGD.
- Гусев П.Ю., Львович Я.Е. Структуризация многофункциональной цифровизированной системы и управление ею на основе оптимизационных моделей дезагрегации ресурсов и объемов деятельности // Моделирование, оптимизация и информационные технологии. 2023. T. 11. № 4 (43). EDN BQZAAO. DOI: 10.26102/2310-6018/2023.43.4.004.
- Гурин Л.С., Дымарский Я.С., Меркулов А.Д. Задачи и методы оптимального распределения ресурсов. М. : Советское радио, 1968. 463 с.
- Львович И.Я., Рындин Н.А., Сахаров Ю.С. Оптимизация распределения ресурсного обеспечения развития цифровой среды управления в организационных системах // Вестник Российского нового университета. Серия: Сложные системы: модели, анализ и управление. 2021. № 4. С. 106-114. EDN FZEJTS. DOI: 10.18137/RNU.V9187.21.04.P.106.
- Львович И.Я. Принятие решений на основе оптимизационных моделей и экспертной информации. Воронеж : Научная книга, 2023. 232 с.
- Оптимизация цифрового управления в организационных системах: монография / Я.Е. Львович, И.Я. Львович, О.Н. Чопоров и др.; под общ. ред. Я.Е. Львовича. Воронеж : Воронежский институт высоких технологий, 2021. 191 с. ISBN 978-5-4446-1550-8.
- Львович И. Я., Львович Я.Е., Фролов В.Н. Информационные технологии моделирования и оптимизации: краткая теория и приложения. Воронеж : Воронежский институт высоких технологий; Научная книга, 2016. 444 с. ISBN 978-5-4446-0836-4. EDN ZUZDNN.


