Оптимизационное моделирование процесса многовариантной структуризации при управлении в цифровизированной организационной системе

Цифровизация организационных систем приводит к тому, что эффективность принятия управленческих решений существенным образом зависит от возможностей цифровой среды управления, которая объединяет технические и программные средства в единый комплекс. При этом эффективность такой цифровизированной системы определяется соответствием показателей установленным требованиям за определенные интервалы времени [1; 4; 5]. Для перехода от одного этапа к следующему требуется стадия развития системы поддержки управленческих решений по двум причинам:

• •    происходит снижение функциональности эксплуатируемых компонентов ниже критического уровня;

• •    возникают новые задачи управления, требующие включения в цифровую среду соответствующих компонентов.

В целях развития цифровой среды управления организационными системами управляющий центр привлекает дополнительное ресурсное обеспечение:

• •    для интеграции новых компонентов;

• •    замены эксплуатируемых компонентов с идентичной функциональностью, если она не поддерживается новыми компонентами.

Целью работы является формирование моделей и алгоритмов процесса выбора компонентов цифровизированной организационной системы, которые максимальным образом будут обеспечивать выполнение требований управляющего центра к показателям эффективности организационной системы. Для достижения этой цели необходимо решить следующие задачи: трансформировать принципы многовариантной структуризации, предложенные в [3], в последовательность вычислительных и оценочных операций, позволяющих определить двоичные и ранговые оценки степени соответствия компонентов цифровой среды экстремальным и граничным требованиям цифровизированной организационной системы; определить размерность задач компонентной оптимизации, математические функции экстремальных и граничных требований задачи; определить энтропийные оценки, необходимые для организации H -релаксационного итерационного процесса.

Оптимизационное моделирование процесса многовариантной структуризации на компонентном уровне

Согласно принципу компонентной оптимизации [2] оптимизационная модель многовариантной структуризации на компонентном уровне направлена на ограничение разно- образия множеств реализации g -го компонента wg = 1, Wg до некоторого редуцированного множества w = 1, W , g = 1, G. При этом редуцированные множества должны включать реализации w, в наибольшей степени соответствующие по своим показателям yw j, j = 1, J, wg = 1, Wg граничным

У ) = fj ( x m ) ^ У °j> ^j = 1, J .

и экстремальным требования к показателям цифровизированной организационной системы. Кроме того, эксперты управляющего центра выделяют один или несколько наиболее значимых показателей, для которых требования (1) трансформируются в экстремаль- ные Vj (xm )^ min, j1 =1, J 1 с использованием функции xm о                                  о

1 = p j 1 — f j 1 ,        У 1 " У л,

т j ⁽ x m ) |

1       10, в противном, случае, где j1 = 1, J 1 e 1, J - нумерационное множество показателей, к которым предъявляются экстремальные требования (2).

Источником определения такого соответствия в форме двоичных

' 1,

c mj   ^с

0,

если реализация компонента соответствующая m-альтернативной переменной способству ет выполнению условий (1), (2)

в противном случае, m = i;M, j = 1J;

или ранговых а ■ =1 mj

-

P mj

Z J . f m

m = 1, M , j = 1, J ,

оценок является экспертная информация.

Рассмотрим, каким образом использовать экспертную информацию для определения двоичных оценок. Формируются G наборов, фиксирующих мнение эксперта:

• 1 1,    если w_g -я реализация g-го компонента влияет на достижение)-го требования, 0, в противном случае,

  
  

w g = 1 W , g =i^ G , j = 1J .

Оптимизационное моделирование процесса многовариантной структуризации ...

На основе (5) и с учетом правила большинства при экспертном оценивании определим интегральную оценку g -го компонента:

J 1

_ 11, если^Cwjj >-J, wg |                j=1

• 1 0,    6 противном случае, w_g = 1W , g = 1 G .

Тогда степень влияния m -й альтернативной переменной, соответствующей wg -реализации g -го компонента, будет вычисляться как emj = EWgeWgj .                                                   (6)

Для вычисления ранговых оценок к экспертному оцениванию привлекается группа d = 1, D экспертов. С учетом выполнения условий согласованности экспертов определяются значения рангов каждой реализации w_g = 1, W_g по j -му требованию к показателям эффективности цифровизированной организационной системы:

P w_gj , W g = 1 W , g = 1 G , j = 1 j ,                             (7)

которые определяют значимость w_g -й реализации g -го компонента для выполнения j

• -го требования: наиболее значимая - p _w j = 1 , наименее значимая - p _w j = W .

wgj                                         wgj      g

На основе (7) определяются коэффициенты значимости w_g -й реализации g -го компонента соответствующей m -й альтернативной переменной:

P wj

a mj = 1 - „ W g ----, m = 1, M , j = 1, J .

P wj

^^ Wg = 1    g^j

Для формирования оптимизационных моделей, включающих альтернативные пере-[1, менные xm =< , m = 1, M , необходимо определить размерность нумерационного множе ства m = 1, M в соответствии с условием

H ( B ) > H ( A ) ,                                      (9)

где H – обозначение величины энтропии. Следует обеспечить сохранение разнообразия процесса многовариантной структуризации A в пространстве вариантов редуцированных множеств S l , l = 1, L при реализации процесса многовариантной структуризации B в пространстве альтернативных переменных.

На начальном этапе процесса многовариантной структуризации A принимается равномерным распределение вероятностей формирования вариантов S l , l = 1, L , что приводит к зависимости энтропийной оценки H ( A ) от числа вариантов L . Многовариантная структуризация на компонентном уровне основана на делении множеств w_g = 1, W_g , g = 1, G , на два подмножества - редуцированное w _g = 1, W g и остаточное. При этом число возможных вариантов

TV    ——

L = 2 g , g = 1, G .

Тогда

H_g ( A ) = W g lg 2, g = 1 G .                               (10)

На начальном этапе процесса многовариантной структуризации B принимается равномерное распределение значений альтернативных переменных для g -го компонента

P mg = 0,5, m g = 1, M g g = 1, G .

Тогда энтропийная оценка в соответствии с (10)

H g ( B ) = M g lg 2.                                 (11)

Исходя из условия (9) и энтропийных оценок (10), (11) размерность оптимизационной модели при многовариантной структуризации на компонентном уровне можно записать как

M g = W g , g = 1 G .

Поскольку для всех компонентов g = 1, G формирование редуцированного множества w g = 1, W g осуществляется идентично, далее будем обозначать при окончательном формировании оптимизационных моделей множество альтернативных переменных m = 1, M .

Определившись с размерностью множества альтернативных переменных и характери- зацией влияния соответствующих им компонентов wg,g = 1,G, перейдем к формированию экстремальных и граничных требований. Непосредственные математические конструкции, отражающие требования, различны для оценок влияния (6) и (8).

В случае оценок (6) имеет смысл использовать их при формировании граничных тре бований, разделив на две группы, - соответствующие требованиям (2) j1 =1, J 1 и требованиям (1) j2 = 1, J2 , где 1, J 1 u1, J2 =1, J . При этом каждая реализация wg -го компонента, включаемая в редуцированное множество

W g = 1, W g , должна обеспечивать влияние на

выполнение не менее C_j требований (2) и C_j требований (1): M

Z c m, X m >- C_k,j 1 = U;

m = 1

M bmj, 2 Xm . C2 2,j 2 = U.

m = 1

Тогда экстремальное требование направлено на минимизацию числа компонентов

W g , включаемых в редуцированное множество:

M

^ x m ^ min .

xm m=1

Объединив (12) и (13), получим следующую оптимизационную модель:

Оптимизационное моделирование процесса многовариантной структуризации ...

M

Z x m m = 1

^ min . x_m

M

^^cmj ^Xm ^— C j 1 , ^j1 = 1, J 1 ;

m = 1

M

D m 2 X m — C 2 , j 2 = J • m = 1

[ 1,      -----

^Xm ⁼| 0 m ^{= 1} , ^M

В отличие от модели (14), где данных c_mj , C_j , c_mj , C_j достаточно для ее построения, оценки (8) позволяют сформировать только экстремальное требование, которое заключается во включении в редуцированное множество тех реализаций w_g g -го компонента, которые обеспечивают наибольшее влияние на выполнение j -го требования. Поскольку

имеем j 1 = 1, J 1 экстремальных j ₂ = 1, J ₂ граничных требований, получаем многокритериальную задачу

M

Z a mA x m ^ max , j 1 = 1, J 1 , m = 1

M

Z a mj 2 x m ^ max , j 2 = 1, J 2 .

m = 1

Граничные требования связывают задачу компонентной оптимизации с задачей ресурсной оптимизации по следующим характеристикам:

U W , w g = 1, W g , g = 1, G — ресурсное обеспечение, требуемое для ввода в эксплуатацию и поддержание функциональности w_g -й реализации g -го компонента;

U g , g = 1, G — ресурсное обеспечение, которое установлено для ввода в эксплуатацию и поддержание функциональности g -го компонента.

Будем считать, что альтернативные переменные x_m , m = 1, M соответствуют множеству

реализаций W g = 1, W g g -го компонента. Тогда граничное требование имеет вид

где

M

Z x_m соответствует числу

M

Zum Xm m =1

^ Z X m U , I m = 1 J

компонентов, включаемых в редуцированное множество.

m = 1

Объединив (15) и (16), получим следующую оптимизационную модель:

M

T a j ^Xm ^ max , j 1 = 1 J 1 , m = 1

M

T a mj 2 ^Xm ^ max , j 2 = 1, J 2 .

m = 1

M

- TXm U i j

T u rn X m m = 1

| i, —

^Xm =| 0 m = 1, ^M

Следующим этапом после формирования оптимизационных моделей (14), (16) является итерационная реализация многовариантной структуризации. Для обеспечения Н -релаксационности при переходе от к -й итерации к ( к + 1 ) -й процесса А используется условие

LL

-Tpk+1 lgpk+1 --Tp №, l=1

где p_l^k определяется на k -й итерации по формуле

M1

pm, = Pkm , pl =Пp^ П (1-PXm ), m=1    m=M 1+1

где m = 1, M 1 - нумерационное множество альтернативных переменных, для которых принято значение x_m = 1 , m = 1, M 1 , - нумерационное множество альтернативных переменных, для которых принято значение x_m = 0 процесса B :

M

T [ p i + lg p k + +^{( 1} - p^¹ ) lg ^{( 1} - p i + ) ]^- m = 1

M

T ^[ p X m lg p l m ⁺ ( 1 - p l m ) lg ( 1 - p l„ ) ] '

m = 1

Энтропийные оценки (18), (20) используются для проверки правила останова

H K ^{- 1} ( А ) - H K ( А ) - Y , H K ^{- 1} ( B ) - H K ( B ) - Y ,

итерационного процесса при k = K . После останова на основе альтернативных перемен ных xm = 1 формируются редукционные множества реализаций компонентов iwg =1, Wg, g = 1, G, что и является результатом многовариантной структуризации на компонентном уровне.

Структурная схема оптимизационного моделирования процесса многовариантной структуризации на компонентном уровне приведена на Рисунке.

Оптимизационное моделирование процесса многовариантной структуризации ...

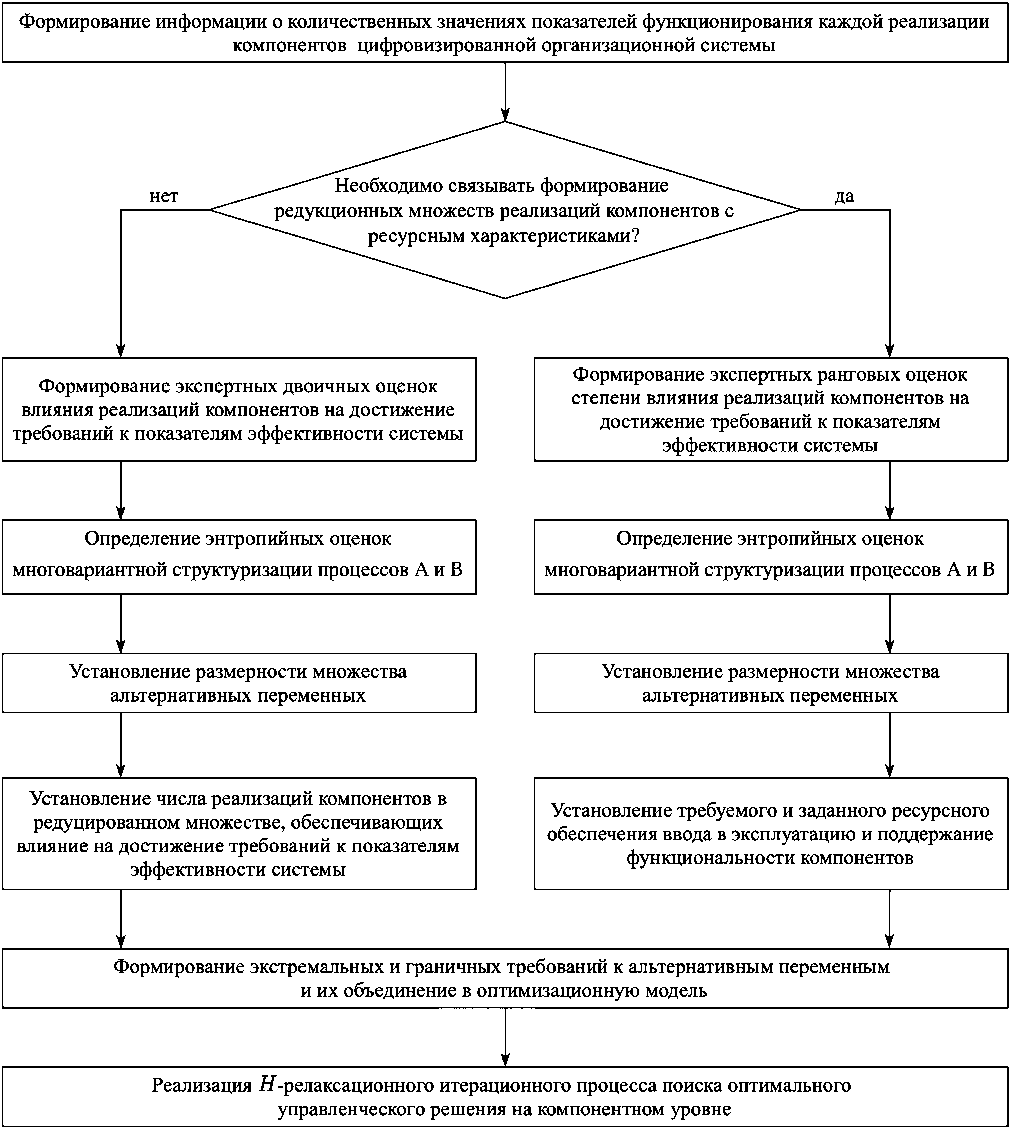
Рисунок. Структурная схема оптимизационного моделирования многовариантной структуризации на компонентном уровне

Заключение

Необходимость развития цифровой среды управления, интегрированной в деятельность организационной системы, требует для этих целей привлечения управляющим центром дополнительного ресурсного обеспечения и его распределения между компонентами, входящими в эту среду, и временными интервалами, определяющими дискретные моменты времени мониторинга показателей эффективности и принятия решений. При формировании оптимизационных моделей процесса многовариантной структуризации необходимо организовать экспертное оценивание реализаций компонентов цифровой среды, включаемых в редуцированное множество так, чтобы определить двоичные и ранговые оценки степени влияния этих реализаций на соответствие их показателей экстре- мальным и граничным требованиям цифровизированной организационной системы. Проведя энтропийную оценку размерности альтернативных переменных, необходимо сформировать критерий и ограничения задачи компонентной оптимизации. Построенная оптимизационная модель позволяет осуществить H -релаксационный итерационный процесс поиска оптимального управленческого решения и обеспечить развитие компонентов цифровой среды для максимального удовлетворения показателям эффективности цифровизированной системы, заданных управляющим центром.