Оптимизационные модели коммерческой деятельности банка и финансовой поддержки малого бизнеса

В первом параграфе данной работы будет исследована задача максимизации чистой прибыли банка-монополиста (или банков равных возможностей) на рынках кредита и депозита, а в следующем параграфе рассматриваются модели кредитирования малого и средного бизнеса и два конкретных примера. Нужно заметить следующие два обстоятельства, связанные с кредити-рованием малого и средного бизнеса. Во-первых, кредитную организацию, которая кредитирует определенное количество представителей малого и средного бизнеса по какому-то проекту, можно считать фирмой-монополистом, так как последние обслуживаются только ею. Во-вторых, в этом случае кредитная организация наиболее заинтересована в максимизации прибыли своих заемщиков, так как от этого зависит успех всего проекта, следовательно, прибыльность кредитной организации в результате осуществления данного проекта. Именно эти предложения позволяют рассматривать оптимизационные модели.

§1. Моделирование эффективности коммерческой деятельности банка-монополиста

Здесь рассматривается математическая модель, которая может быть использована

1 Работа выполнена при финансовой поддержке РФФИ (совы 07-01-90101).

для описания эффективной коммерческой деятельности только такой финансовой организации, которая является банком-монополистом (системой банк равных возможностей) на финансовом рынке. Она очень полезна для такой кредитной организации, как сберегательно-кредитный кооператив, который имеет определенное количество клиентов, обслуживаемых только ею.

Здесь мы приводим самую простую статистическую модель обращения части наличных денег С>0 граждан (организаций, компаний) через банк. Количество денег, которые граждане хотят хранить в данном банке или взять в кредиты, конечно, зависит соответственно от депозитной р>0 и кредитной л>0 ставок банка. Обозначим через Др):0<Др)<1 и g(A): 0 Дд) и g(A) показаны на рисунках. /(А) и g(4) являются соответственно строго выпуклой возрастающей и строго вогнутой убывающей функциями, удовлетворяющими условиям g(0) = 1 /(0) = 0, g (0) - /'(О) = 0. Это

Бурятский Государстаенвый УСТНЫЙ пр№Г*

НАУЧНАЯ БИБЛИОТЕКА

заявка

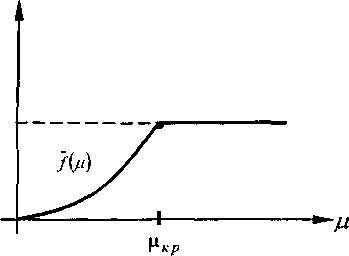
означает, что при малой кредитной ставке по мере её возрастания число граждан, желающих получить большие кредиты, медленно убывает, зато при малой депозитной ставке по мере её возрастания число граж-

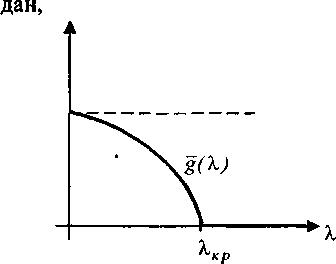
желающих вкладывать все свои деньги в банк, медленно убывает. Тогда вероятности сбережения и получения в кредит всех имеющихся денег соответственно выражаются формулами:

/(д) = тт(7(А),1);

g(Z) = max(gW,0).

р^^, являются теми критическими значениями ставок, когда соответственно все хотят отдать свои деньги в банк или отказаться от кредита. Допустим так же, что все затраты банка, кроме депозитной ставки, будем считать пропорциональными Д-й части суммарного дохода, 0<Д<1, а а-я часть депозита останется в Монголбанке как резервный капитал. Тогда имеем: количество депозита /(а) • С; количество кредита (l-a)pg(2)/Gu)C, т.е. (1-а)/>-я часть депозита выдается в кредит. Число О < р й 1 показывает, какая доля актива банка идет на ссуд. Доход, получаемый от кредитирования, (1 -а^рХ• g(A)/(//)-С, Р -я часть которой идет на расход, связанный с депозитом: p-f(p)-C. Следовательно, задача максимизации чистой прибыли банка выражается как

П(а^) = С((1-рХ'-а)Хх xgUV(P)-p-/(P))*^ max, (I) /з>0,Я>0.

Так как g(^)-0 при Л>^, и /(р) = 1 при ц>р_кр. то П(/дЛ)->0 при //~->оо, 2~>оо, следовательно, решение (р*,Я*) задачи (1) существует. (^*^(^)) = = 2g'(X) + g"(X)-X<0 на [0,Л^], и поэтому единственное решение 0 <  X* < X находится из условия g (X) ■ X + g(X) = 0. Это следует, из того, что функция a(X) = X-g(X) положительна и строго вогнута на [0Д_р), причем, «(О) = орХ^ ) = 0 . Для нахождения р" , мы должны решить следующую задачу.

Д^) = ((1 - ДХ1 - а^рХ* X xg(r)/(/z)-/z-/(^»^max, р>0 (*)

В вышеописанной модели предполагается, что, собрав деньги вкладчиков с некоторой ставкой р , банк часть из них раздает в виде кредита заемщикам со ставкой X . При д = д', Л = Л* данный банк или кооператив должен получить наибольший чистый доход.

По данным 2005 г., в Монголии функционируют более 300 сберегательнокредитных кооперативов. К сожалению, в последнее время часть из них, желая приобрести побольше вкладчиков (следовательно, в конечном счёте побольше денег), обещала неправомерные высокие депозитные ставки, соревнуюсь как бы между собой. Это привело в конечном счете полному краху некоторых из них, которые просто не в состоянии выплатить деньги вкладчикам, вложив их деньги в недвижимость. В этом смысле данная модель может быть полезной, ибо показывает, какая гармония должна существовать между депозитной и кредитной ставками.

Числовой пример. Предположим, что функции f(p) и g(^) имеют соответственно следующие виды:

/(p) = ap\a>0, g{X) = t-bX\b>0.

Найдем р_кр и Х^:

=1                ,

1-М’=0 => л,^.

Следовательно, имеют место формулы: Лд) = 7(A) при Д._Р<^ ,Лд) = 1 при

’ 8<^Л) = ^W при ^<^j >  gU) = 0 при А,^ •

Для нахождения оптимальной кредитной ставки Я* мы должны решить следующее уравнение на

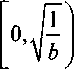
(2g(2))' = g'(^ + g(2) = 0,

-2М2 +1 - 6Я2 = 0 .

Откуда находим, что Я' = ^^ .

Тогда, учитывая (*), для нахождения д имеем следующую экстремальную задачу:

^(А) =

Г 2           /Т

= -(1~а)р(1-Д) —--Д -/(а) —> max, N3b )

рШ.

Введем обозначение

• 3               V до

Тогда после простых вычислений легко получить формулу

• — В, В-^< — а-В²,

.   3         Na 27

А

Na 27

Полагаясь на квартальные данные об внутреннем валовом продукте, суммарных показателях кредита и сбережения, взвешенных размерах кредитной и депозитной ставок банковской системы Монголии за 2002-2006 гг., для функций J(p) = ap2, а>0, £(Я) = 1-6Я2, 6>0, и фиксированных параметров а =0.05, Д = 0.3, р-0.6 мы получили следующие оценки:

а = 0.0027 , b = 0.00056 , д_кр =19.24 ,

Д., = 42.2, р = 19.24, Я* = 24.4 .

§2, Кредитирование малого бизнеса и поддержка его малодоходной части Здесь рассматриваются     задача максимизации суммарного    дохода определенного количества заемщиков и максиминная задача поддержки их малодоходной части.

• 1.    Максимизация суммарного дохода малого бизнеса. Пусть имеется Д представителей малого и среднего бизнеса, которые нуждаются в финансовой поддержке. Допустим, что некая кредитная организация взялась за кредитирование этих бизнесменов, выделив при этом сумму М денег. Обычно такая работа выполняется по целовой программе или проекту для того, чтобы кредитируемые организации выпускали однотипные продукты. Пусть к -й заемщик, взяв кредит в количестве х*, может выпускать продукцию стоимостью Д(хД, затратив при этом (с_А + Д)х_к денег, где ц > 0 -кредитная ставка, усредненная за кредитный срок. Мы ограничимся случаем, когда известна цена капиталов (мы здесь предполагаем, . что потенциальные заемщики для получения кредита имеют возможности подставить кое-что или получить гарантию надежных спонсоров и т.д.), подставленных под залог заемщиками E_v k = \,....,N. Тогда будем иметь следующую задачу оптимизации:

• 2.    Поддержка малоимущей части населения посредством микрокредита. Около 96% из занимающихся бизнесом организаций нашей страны составляют представители среднего и малого бизнеса, причем они производят 60% внутреннего валового продукта. Поэтому в последние годы в Монголии все более широкий размах приобретают так называемые микрофинансовые услуги бедным слоям населения. Такого рода деятельностью занимаются не только банковские организации, но и небанковские финансовые организации и сберегательнокредитные кооперативы. Среди м икрофинансовых услуг главное место занимает кредитирование малоимущей, т.е. малодоходной, части населения. Причем этому вопросу государство уделяет самое серьезное внимание. Подтверждением тому является организация национального конгресса по микрофинансированию, проведенного в ноябре 2004 г. в Улан-Баторе. Подробную информацию о микрофинансе, микрокредите и микробизнесе можно найти в монографиях: “Бичил зээл ба бизнес эрхлэгчдийн ундэсний чуудган” (1994), “Монгол дахь бичил санхуугийн дэд салбарын судалгаа” (2004).

У [Л (^) - (^ + а)^ ] ^ ^тах >  *-1

N

Ух^=А/, 0 < хх < а • Ек, k = где а >0 задается кредитной организацией. Для переменных xt, принимающих реальные значения, решение этой задачи характеризуется так называемой обобщенной леммой Гиббса, доказанной нами. Эта задача при реальных значениях х, может быть решена с помощью алгоритма, использующего обобщенную лемму Гиббса, причем в случае строгой вогнутости функций /ДхЛ этот алгоритм является конечным. В случае, когда xt принимает конечное число значений,

20 нужно использовать метод динамического программирования, описанный в [6].

Микрокредитом называется обслуживание бедных слоев населения в виде ссуд в малых размерах. Среди иностранных спонсоров, поддерживающих микрокредит в Монголии, можно назвать следующие организации: USAID, World Bank, CGAP, ADB, IFC, JICA, GTZ, IFAD и UNDP.

А государственная политика поддержки малоимущей части населения осуществляется главным образом через Монголбанк.

Когда проект кредитирования осуществляется по правительственной программе или по инициативе какой-либо иностранной организации доброй воли, то больше всего внимание уделяется малоимущей части среднего и малого бизнеса, т.е. микробизнесу. При этом речь не идет о снижении кредитных ставок и предоставлении других льгот малоимущим, а имеется в виду поддержка коммерческой деятельности тех, кто в этом больше всего нуждается. Обычно бедняки не имеют капитала, который можно было отдать в залог, но вполне способны провести коммерческую деятельность. При такой постановке вопроса мы должны решить следующую максиминную проблему:

mm (Л <^хк)"<Ек + АХ) ^ max,

N

^xt=M, х^йО, £ = !,...,А, t=i где xt - количество кредита, предназначаемое к -му заемщику. Эта модель представляет собой классическую максиминную задачу распределения ресурсов [3], и решается известными алгоритмами: когда х^ могут принимать реальные значения, она решается с помощью алгоритма, основанного на классической лемме Гиббса и теоремы Гермейера, а когда хк принимают целочисленные значения, она решается с помощью метода динамического программирования [6].

При учете кредитного залога мы получаем следующую задачу:

™ (Л (^ ) - (с* + А)^ ) -> max,

^x_k=M"_s 0<х_к<а-Е_к, k-^,...,N. гл

Здесь Е_к - количество капитала / -го заемщика, аЕ_к - доля капитала Е_к, 0<а<1, такая, что кредитная организация не может дать i -му заемщику больше денег, чем аЕ_к . С помощью обобщенной леммы Гиббса можно доказать теорему, характеризующую решение этой задачи, которую можно назвать обобщенной теоремой Гермейера для максминных задач с ограничениями. В случае, когда х_А. принимают целочисленные значения, нужно использовать алгоритм нахождения решения задачи из пункта 1 с добавлением метода штрафов.