Optimization of A-star search algorithm

Today, mobile robots are engaged in various tasks related to the delivery of goods, reconnaissance, automated patrol, and search and rescue operations. Autonomous mobile robots must be able to plan global and local motion paths, create a three-dimensional model of the environment, determine its location in space and control actuators to keep motion along the planned path [1].

The path planning is an important and non-trivial task. Therefore a lot of studies are currently underway in this area. Various algorithms are being developed for calculating the path both in a static environment with known obstacles and in unknown and dynamic environments where it is impossible to have prior complete information that can be given to the robots before operation [2–8].

One of the most effective path finding algorithms in a static environment, widely used in practice, is the A-star algorithm [9, 10]. It is a modernized version of Dijkstra's algorithm. A-star allows us to calculate the path at the lowest cost from the initial peak to the final in a weighted directed graph. The least path cost in the algorithm means the shortest distance between the selected points.

However, if we are dealing with real objects that have some limitations (kinematic, controls, etc.) or when introducing additional information about the map of the area and taking into account the costs of overcoming them (the cost of maneuvering, overcoming hills, etc.) – the considered algorithm can lead to a non-optimal solution of the problem for given conditions [11, 12]. Therefore, for practical application, the algorithm must be optimized for real conditions including a number of restrictions [13]: kinematic restrictions (maximum speed, minimum turning radius, etc.), control limitations (remote control along the motion path), restrictions on the degree of danger of the chosen path and others.

1. Implementation of A-star algorithm in MATLAB

For research, the A-star algorithm was implemented as a computer model in the MATLAB modeling environment [14, 15]. The model’s interface is a 20 x 20 polygon field where the starting point

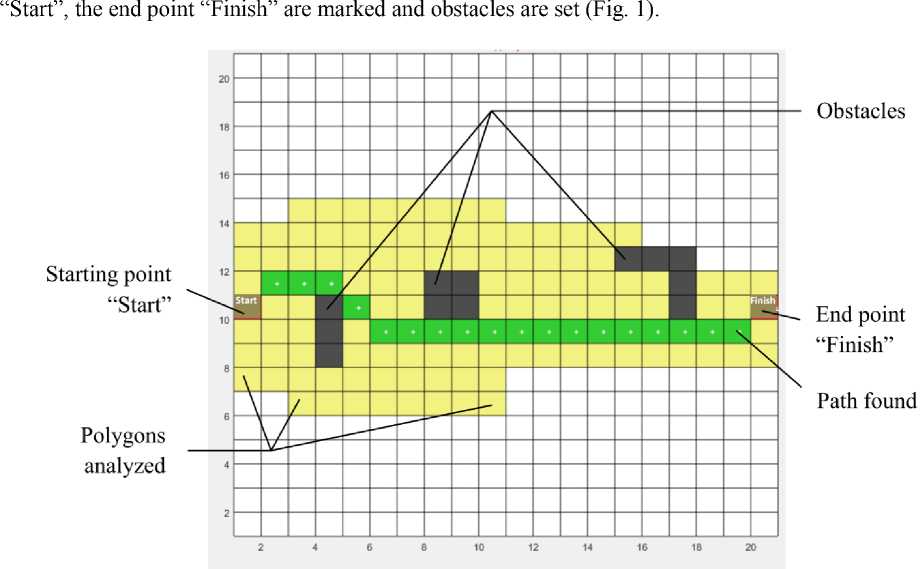
Сomputational time, ms31.3

Polygons analyzed126

Path length (in polygons)19

Number of turns3

Fig. 1. Example of path calculation

The path calculation algorithm works as follows.

• 1.    In the first step, two lists of polygons are created: a) pending analysis, b) analyzed. A starting point is added to the list of pending points.

• 2.    For all neighboring polygons that are no obstacles, the coefficient F n is calculated:

• 3.    All enumerated polygons are recorded in the list of pending analysis. Next, from this list, the polygon P _{min Fn} with the lowest value of F_n is selected.

• 4.    Then, for each of the P i ranges adjacent to it, with the exception of obstacles, the conditions are checked:

F n = G n + H n ,                                                                            (1)

where G n is the cost of transitions from “Start” to the current point, H n – the remaining distance from the current point to “Finish”, and the number of the parent polygon from which the transition was made is remembered.

If P _{min Fn} is the final polygon, then the route is found and the algorithm is finished. If not, P _{min Fn} is moved from the pending analysis list to the analyzed list.

• a)    if P i is included in the list of analyzed polygons, then skip the calculation, if not, go to point b);

• b)    if P i is not included in the list of pending analysis, then we add it there by calculating F ni and remembering the link to the parental polygon P _{min Fn} , if P_i is included in the list of pending analysis, then compare the current F_ni with the resultant F_n j for this polygon. If F_ni <  F_n j , then a shorter less expensive, path to the current polygon was found, therefore, replace F nj with F ni .

• 5.    Repeat steps 2 to 4 until the end point of the route is reached.

• 6.    If the list of fields awaiting the analysis is empty and the endpoint is not reached, then the route does not exist.

• 2.    Optimization of algorithm for the number of turns

A-star is optimal in terms of finding a path with a minimum length. The algorithm is modified by adding optimality to the minimum number of turns in the path. For this purpose additional cost coefficients W_n that increase the cost of the path when turning are introduced. In this case, the formula for calculating the cost of the path will be:

F n = G n + H n + W n .                                                                       (2)

The simulation results without optimization are shown in Fig. 2a, with optimization in Fig. 2b.

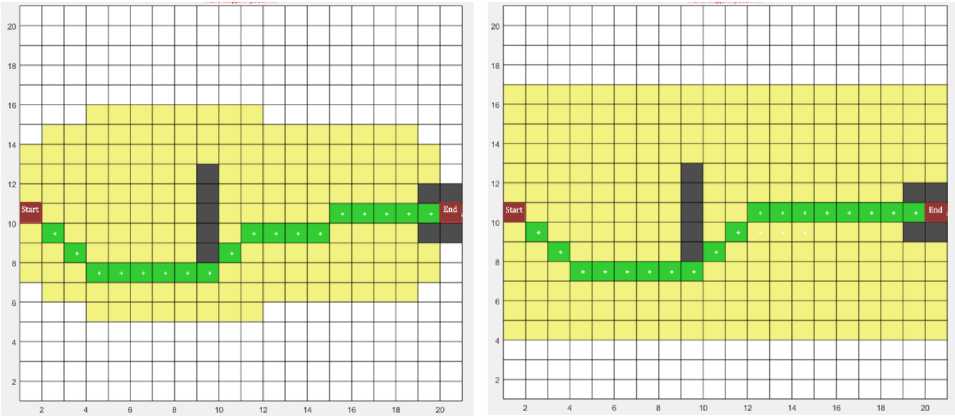
Сomputational time, ms46.0

Polygons analyzed177

Path length (in polygons)19

Number of turns5

Сomputational time, ms62.5

Polygons analyzed251

Path length (in polygons)19

Number of turns3

• а) results without optimization

  b) turn-optimized results

  
  

• 3.    Optimization by complexity or time of the path

Fig. 2. Calculation of the optimal path

The results obtained show that, after optimization, the number of turns was reduced from five to three, while the path length, measured in the number of passed polygons, did not change. At the same time, the number of analyzed polygons increased and, as a result, so did the computational time, but not critically.

This type of optimization is carried out by introducing weighting factors that increase or decrease the cost of passage of the indicated polygons in the field. In practice, the increase in the cost of crossing the polygon corresponds to the complexity of the path along this route (mountainous or marshy terrain, or dangerous area) or the time taken to overcome the path (busy track). Increasing the cost of passage through such areas will allow us to find another way that these areas will avoid, the more the higher the cost of their passage.

Fig. 3b shows the results of a path search in the case when the cost of passing the polygons located in the lower part of the modeling field is doubled compared to Fig. 3a.

As a result of the simulation, the path along the upper part of the field was calculated for polygons with less cost. At the same time, the number of analyzed polygons decreased and, as a result, the calculation time.

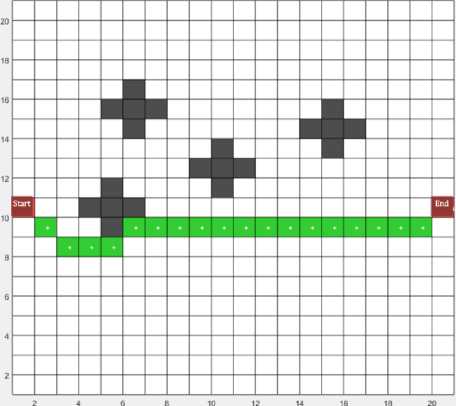
Сomputational time, ms15.6

Polygons analyzed124

Path length (in polygons)19

Number of turns3

Сomputational time, ms 14.8

Polygons analyzed97

Path length (in polygons)19

Number of turns7

• а) results without optimization

  b) turn-optimized results

  
  

• Fig. 3.    Calculation of the optimal path

• 4.    Algorithm optimization based on critical points

The inverse solution of the previous problem can be used in cases where it is necessary for the path of the mobile robot to passes through certain areas on the map, even if the path increases. This may be suitable if the mobile robot must constantly keep in touch with control centers or collect information through relay stations installed in predetermined positions. In this case, when planning the path, it is necessary for the mobile robot to be in the coverage area of these stations (Fig. 4).

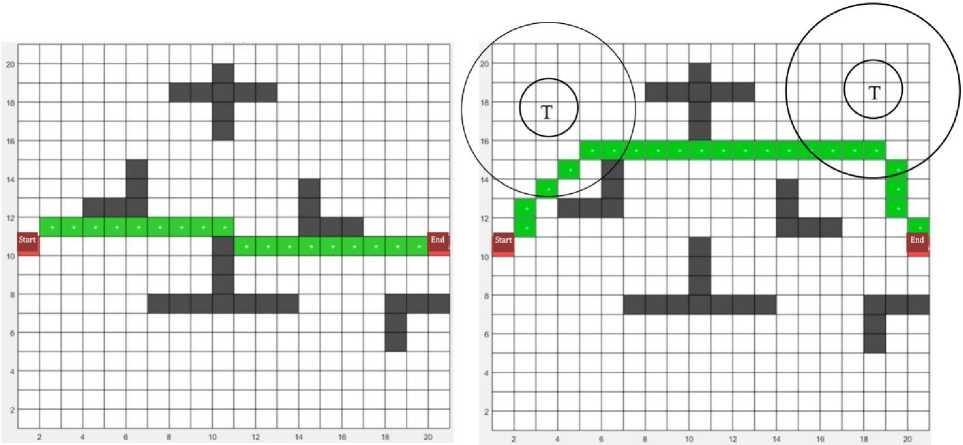
Сomputational time, ms10,7

Polygons analyzed76

Path length (in polygons)19

Сomputational time, ms16,8

Polygons analyzed124

Path length (in polygons)23

• а) results without optimization

  b) turn-optimized results

  
  

• Fig. 4.    Calculation of the optimal path

This can be achieved by adjusting weights. That is by significant increase in weights in the areas of the map (remote from the station by a distance exceeding the range of radio communications with a mobile robot).

Fig. 4 shows the calculations of the optimal path in the presence of two relay stations indicated on the modeling field by the symbol “T”. As a result of the calculation, we obtained a path (Fig. 4b) that deviates from the calculated shortest path (shown in Fig. 4a), however, this path passes through the polygons which are least distant from those allocated with radio coverage and therefore being more optimal for these conditions.

Conclusion

As a result of the studies, options for optimizing the A-star path planning algorithm for its application in conditions with a limited number of turns, linking to critical points on a map of the area, as well as difficult or dangerous sections are proposed. In most cases, as a result of optimization, the path length and its computational time increase, but not significantly. Moreover, the new path corresponds to the given conditions, is the shortest for these conditions and, therefore, is optimal. The developed model allows us to estimate the time and necessary computing resources spent on calculating the path. On the basis of these evaluations, it is possible to choose path planning method suitable for individual scenario.

Of further interest is the task of optimizing the algorithm with incomplete reliability of a priori information or its absence in some parts of the analyzed terrain map.