Optimization of Parameters at SDN Technologie Networks

Published Online September 2017 in MECS

A characteristic feature of modern science and technology is widely used optimization methods in solving theoretical and applied problems.

Regarding the communications technology the problem optimization is not only the organization but also due to the organization properly, for example, with the maximum possible speed in these conditions or information transfer with minimal probability of error for a given hardware complexity, or of minimal size or costs.

There are following types of problems finding optimal solutions in the theory and practice of communication:

• 1.    Research the task related to search the best possible options for constructing devices, systems and networks (eg, search algorithms, signal processing that maximize signal to noise ratio, or search for signals that minimize the occupied frequency band, etc.).

• 2.    The task of designing where you need to select the optimal equipment parameters (for example, to calculate the filter to provide the specified requirements for its selectivity for minimum order transfer function or choose the location of points in the signal constellation in which there is minimal the distance between points of maximum, etc.).

• 3.    The task of building adaptive devices that selfoptimized and self-organizing in terms of the changing situation, or load changes, will be able to choose the mode that minimizes the loss of one or the other type (channel distortion corrector setting when switched networks, routing packet network connection, etc). [1, 2].

This classification is conditional and is often task that must be solved, can be attributed directly to the two or even three of the above types.

However, the characteristic problems of these options is that some dependence criteria of quality of communication systems of one or more parameters are optimized.

The proper choice of arguments must achieve the objectives criterion of maximum or minimum value.

The solution of complex optimization problems requires establishing relationships and values of the variables that characterize the quality of services, the characteristics and parameters of the incoming flow requirements. Necessary structural definition network settings for a given flow, discipline and quality of service is the subject of solving problems of synthesis of information and communication networks [3].

Application of methods optimization is actually only possible in cases where such practical problem finds the mathematical description. Optimization techniques designed to realize by computer.

A detailed review of the structure of each method allows for each method applied in computer programming, computer equipment using, to many iterative calculations and obtain effective and precise solving optimization problems with set requirements.

Purpose of this research is the construction of a mathematical description of the optimal control system of a software-configured network based on selected quality criteria depending on one or more parameters. The main attention is paid to optimizing management behavior under various external disturbances.

Informatization process taking place in the modern economy, are possible by dramatic changes in information technology, including the development of the global Internet, the spread of Software Defined Networks, SDN, introduction of technologies Internet of Things and Big Data corresponding software [4].

Current status and trends in information and communication networks have shown that the potential increase in productivity, bandwidth networks based on traditional technologies is almost exhausted.

This is associated with rising costs of time for routing, difficulties in network configuration and control flows in it. Especially with the new requirements in the policy of quality of service for high-speed global networks and data centers to the growth of need for virtualization networks.

That is displaying of several logically isolated networks with independent politicians quality of service on a common set of network resources.

By improving the quality and increasing the number of services providing the management information in the management system (MS) is growing rapidly. As a result, MS can absorb the basic network.

Building an effective system of modern information and communication networks requires solving problems of predictive control.

Improving global MS is predetermined by structural changes in the industry and the economy, new trends and priorities in network technology, information activities, the growing influence of digital information and communication technologies in the activities of the industry in general and control systems [5].

Since MS options dynamically change over time, it is possible deviations in the values of the studied parameters. Deviations may indicate the presence of network performance problems, failures in the hardware or software.

The challenge is in order to automatically identification of the behavior of MS according to the reference values. Once this behavior is identified, a monitoring system should automatically generate a message to the operator to draw attention to potential problems.

But using of such method does not allow to detect changes in the behavior of the network in real time and, consequently, provides a low probability determination system failure. Therefore, the use of forecasting techniques in information and communication networks is a particularly urgent problem in critical emergency situations.

Solving the problem of constructing optimal structure for data network management system needs to address such key issues as the choice and justify the purpose of optimization, selection number and composition criteria optimization, harmonization objectives with available capacity that is setting limits and getting the experimental values of quality with regard to restrictions.

Selecting and validation concerning the purpose envisage multi-objective optimization criteria of determination the effectiveness of the control system and target features that more fully reflect the goals of optimization.

• II.    Analysis of Recent Research and Publications

In the works of Steklov V.K., Berkman L.N., Popovsky V.V., Sunduchkov K.S., Lemeshko O.V. proposed modern concept of efficient management of next generation networks; Vorobienko P.P., Lozhkovsky A.G., Aheyeva D.V. – theoretical foundations for efficient streaming technology, particularly through the UA-ITT; Zakharchenko M.V., Klymasz M.M. – principles of effective synthesis mains data that formed the basis of the distributed service data; Globa L.S., Shill A., Jo M., Kryvinska N., Strauss C., Luntovskiy A., Wolf A. – developments in the field of service-oriented telecommunications systems. One of the goals of "modernization" of the classical approach to network architecture is the creation of software-defined networking (PCM, Eng. – Software Defined Networks, SDN), using protocol OpenFlow [1, 6]. Therefore, program-configured network – one of the most "hot" today’s technology that arose in the way of collapse Network [7 – 9].

According to the recommendation ITU-T E.800 [10], quality of service (QoS – Quality of Service), a set of specific parameters relating to the internal structure of the network and determine the quality of its work and characterize the properties of consumer services in terms that are understandable to users.

The whole set of characteristics and service quality of the network is divided into two categories [11]:

• -    primary defined by direct observation at the point of access to services and belong to a certain point of time;

• -    derivatives defined by determination on the basis of one or more primary attributes or averaged over a time interval.

• III.    Main Part

Managing influence of the system management to ensure QoS are reduced to the structuring of information flows and the definition of algorithms for each type of traffic in the nodes of switching [10]. Resource allocation switching units produced using different algorithms buffer memory and prioritization for queuing packets and determination order of their finish.

Having analyzed the characteristics of quality assessment services for information and communication networks criterion for optimum performance can be characterized by the following factors:

K opt = T , P , V) ,              (1)

Where

T = T + T 2 + T 3 ,             (2)

• Т 1 – transit retention;

• Т 2 – retention in establishing a network connection;

• Т 3   – retention the completion of the network

connection.

P = P + P 2 + P 3 + P 4 ,          (3)

where

• Р 1 – probability of a failed establishing a network connection;

• Р 2 – the probability of error;

• Р ₃ – the probability of failure of information;

• Р ₄ – failure probability of completion transport

connection.

v = v + V + V 3 ,             (4)

• V ₁ – the speed of establishing a connection;

• V 2 – speed data transmission;

• V 3 – termination speed of connection.

Thus formed network performance and service quality techniques to achieve telecommunication networks based on:

• a)    type of traffic;

• b)    used transfer protocols;

• c)    type networks.

Thus the number of indicators that characterize the quality of the actual system may be too high. The process of finding the optimal criteria is practically reduced to the solution of quantitative optimization.

That is, there are m indices as K = K ,... K _m) system, and the output parameters of the system becoming a state of equilibrium value x ^* , x ^* , x ^* , which minimize the function F ( x , x ₂,.. x _n; K ,... K_m ) . The quality system can be characterized by the optimum working smoke. Moreover, the resulting Quality Score takes the form:

K = min C F ( K_otp ),            (5)

C ( x ) – restrictions that satisfy the acceptable range of values function F ( x ).

The method of optimization of information and communication network depends on the type of target features, limitations and permissible area (given system of inequalities and equalities) [12].

Optimization problems can be formulated as follows: find a minimum of the min n„ F ( x ) at - C ( x ) restrictions that satisfy the acceptable range of values function F ( x ) [13, 14].

The objective function should be formulated on the basis of existing ideas about the quality of the designed network [15], its value has decreased with improved quality.

Let f – function of n +1 variables f ( x ₀ , x ₁ , ..., x_n ). Its domain of x generated aggregate domain of x 0 , x 1 , ..., x n , for each of n +1 variables; with x_k e X_k . For definiteness we impose that x coincides with the real axis, namely, —»< x_k <« , k = 0,1,..., n . For a function of n +1 variables concept of global and local highs (lows) introduced a similar definition for functions of one variable. One has only to bear in mind that extreme point x , characterized by a set of coordinates as ε-neighborhood concept is more complicated. Thus, unlike the one variable function f ( x ), the function f ( x ) depends on n +1 variables.

To the point's coordinates x ^* , x ^* , x ^* , x ^* function f ( x ^* , x ^* , x ^* ) has local extremes, it is necessary that all its partial derivatives reincarnated at this point to zero [16]. This condition is called stationary condition, often written in vector form:

grad f ( x* ) = 0 or ∇ f ( x* ) = 0,         (6)

Points ( n +1) dimensional space satisfying (6), as in the case of functions of one variable, called stationary. Obviously, the stationary point is not necessarily extreme [8].

To continuously twice differentiable function (n+1) variables f(x) has a stationary point of local maximum (minimum), enough to the matrix of second derivatives (Hessian matrix) was negative- (positive-) defined, that nn  2

expression EE£1—pew was less (or more) ground k=01=0 5xk 8xt at random, real number ^, ^,..., ^, such that ^02 + ^j2 +... + ^2 > 0. Verification signs determination matrix can be made, for example, using the criterion of Sylvester.

Stationary point of function of many variables, which are not extreme point is called a saddle in the vicinity of this point are performed inequality f (x0*, X1 ) ^ f (x0, ХГ) ^ f (x0, xf).

In the simulation of information and communication systems is a very interesting study their behavior under different external perturbations. For the current study approach characteristic disturbances in the structure of the system. It is necessary to determine whether the behavior change significantly as a result of unplanned (including unwanted) changes in management mode.

The practical value of this research is the ability to timely predictions of emerging inconsistencies in the structure of the system under consideration, determining the moment of falling into a critical area that serves as a signal for the development and implementation of measures that can affect the facility, avoiding falling growth rate of efficiency. In other words, result this study to predict the moment of transition systems new technologies, promote the emergence of new technologies within the elderly, influence the course of technological progress.

Let the dynamic system behavior is described by a set of ordinary differential equations:

r = fi (rv...r;aP...,ak), i = 1,n, where R = (r1,...,rn) - state (point) system, ai - the parameters of the system. Then the stationary state is out of the equation f (rv...r„;ai,...,a) = 0, i = 1,n. (*)

If r = a i ( i = 1, n ) - a special point - end solution for the system of equations (*), then the stability resulting steady state is decided by calculating the roots of the characteristic equation

P ( X ) = det { A_t - Xi . } = 0, A k =| | , 8 _й k (**) I ^{d r} k ) rs = as 1 0, i * ^k .

Stationary state is stable if R e X i <  0 ( i = 1, n ) , where X i - the roots of (**). The points, which violated conditions of stability are called critical or extreme.

Examining the behavior of saddle point near the equilibrium state come to a conclusion that this special point is always unstable.

For this we consider the basic theory of systems described by two differential equations of second order. This two-dimensional system can be represented as follows:

where Y – stationary value Y .

To investigate the system (7) compare the properties of dissipative and conservative systems based on the study of the properties of the operator:

c

b d

So, aware that for any conservative Hamiltonian system exists - so that the system is transformed and gets the following form:

dY=f (Y, Y )=8-, dt         27d

.

. = f2 (Y1, Y2 ) = -Ц dtd

In the linear approximation we have d/1 = 52 H = -df^

5 Y  5 Y 5 Y5 that is a = -d or Sp (tr) L = 0.

In view designations ц = Sp ( tr ) L - should matrix of operator L , A - determinant of a matrix operator L , characteristic equation is as follows:

^2 — pto + A = 0.

Integrating this equation, it is easy to obtain

П = c_Q | ^|в ⁰, where e₀ = — ² . ° _x

Assume that —₂ - big root of the characteristic equation.

If — ₂, — one sign, we are dealing with integral parabolic curves. If ( — , — ₂) - negative, that as follows from of equations

I dY dY = f. ( Y Y 2 ) •

. ^> f 2 ( YY )

To determine the type of particular points for the roots of the characteristic equation of two-dimensional system (7), we introduce the following notation:

Z = >  - > 1(s) ;   Z 2 = >  - Y 2(s) ,

|^ , | n decreases with time.

Representing point of time approaching origin of coordinates but it never reaches a final moment, because it would be contrary to the Cauchy theorem, which states that through each point of the phase plane is only one phase trajectory of the system (11).

This particular point through which the integral curves is similar to as the family of parabolas (у = сох™, to < 0)

passing through the origin of coordinates is called a node.

It is easy to see that the state of equilibrium, which corresponds to the node (at to < 0, to < 0 ), Lyapunov stable as depicting point of all integral curves moves to the origin (stable node – Fig. 1 (a)). If the to > 0, to > 0, then П\, |^| increase with time, the depicting point away from the origin (unstable node – Fig. 1 (b)). In general, the behavior of the integral curves around the equilibrium state will not change, but relevant due coefficients а, в, у, 5, may not coincide with the origin. Below are examples of stable and unstable units (Fig. 2).

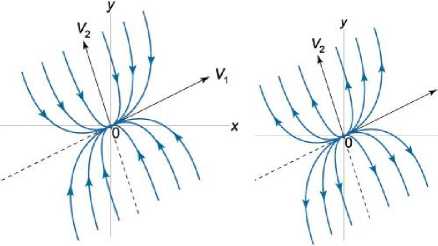
(a)                      (b)

Fig.1. The image on the phase plane particular points: a) stable node; b) an unstable node

Considered integrated family of curves has a single singular point at the origin, through which only two integral curves are asymptote. This is called a singular point of saddle . General view of the seat shown in Fig. 2.

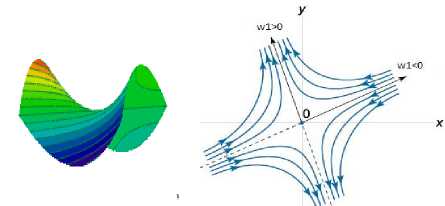
(a)

(b)

Fig.2. Image singular point of saddle:

a) on the plane of canonical coordinates ^, 7/ b) on the phase plane catastrophe theory in mathematical description of the processes occurring in the management system information and communication systems allows to analyze and ensure system reliability, relatively unpredictable changes in the structure of the system and operating conditions [18]. Using catastrophe theory can provide background information as topological map changes characteristic points and areas studied physical processes [19].

Unlike classical methods of mathematical analysis [20, 21], which allows you to explore a smooth continuous processes, catastrophe theory is a versatile research tool intermittent transitions, breaks, sudden qualitative changes in the behavior of the system.

Consider a system with two control parameters k 1 and k 2 – bandwidth and delay control signal.

Write disasters function depending on the number of control parameters and number of variables. Analyze the critical point of the objective function, that is the point where not only the first derivative function is zero, but zero and higher order derivatives.

Its stable state corresponds to one of the seven elementary catastrophes resulted in. This disaster has called "collection", where x – variable described by differential equation:

F ( x , k , k ₂) = R + s f = ^x ⁴ + ^ kx 2 + k-iX ,

where F ( x , k , k ) – objective of functions.

In function F dimension x ⁴ is a "sprout" catastrophe that is resistant to external changes in the management kx ²

system. Magnitude sf = k2x +     - random external perturbation.

Look for unstable state management system, according to the control parameters and the optimal ratio parameters.

Separatrix boundary is a steady state system. Solution of the system of algebraic equations x3 + kx + k2 = 0

• 3 x ² + k = 0

6 x = 0

gives separatrix equation k1

^k 2   |

2 )

= 0,

Explore depicting behavior near the point of equilibrium. At to >  0, to <  0 this point is located on ^ axis will move away from the origin, and posted on 7 7 axis – infinitely closer to origin of coordinates before reaching its end in a moment. So singular point of saddle is always unstable.

Using bifurcation theory of dynamical systems and corresponding lines {LS, MS} (Fig. 3)

Disaster area "assembly" shown in Fig. 3. The hatched portion of the surface corresponds to unstable equilibrium position, others – sustainable. Point S is a critical point of the system. If the system is a starting point and setting point A gradually increases, the system state changes along DIA – at point C is jump. When you return to the starting position will change the state of the other way – VEF. At the same time, a special control panel possible a smooth transition from A to B along the ADV. The hatched portion of the surface corresponds to unstable, precarious status.

probability of error and b – the delay of the control signal, c – the number of failures. Its steady state corresponds to one of the seven elemental disasters cited in [22, 23]. Target function will look like:

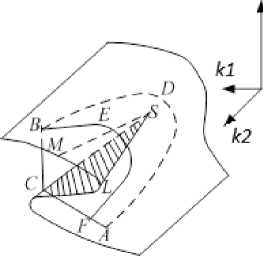
Fig.3. Disaster Area "assembly"

F ( x , a , b , c ) = -x + - ax +— bx + cx .     (15)

This catastrophe is called Сatastrophe dovetail (Fig. 4). Сatastrophe dovetail tail can be defined as the set of all points ( a , b , c ), such that the polynomial has a multiple root. In this surface there is an edge of the return (B, Fig. 4) and the line of self-crossing (C, Fig. 1) [22].

Critical points are obtained by equating the first derivatives of F ( x ; a , b , c ) to zero:

d F    4,2

= x + ax + bx + c = 0 . d x

To adjust control parameters k ₁ and k ₂ of equations can define their proportion: k_Y = - 3 x 2 , k₂ = 2 x ³ .

The set parameters ( k , k ₂) in D = 0 pairs to form a plurality of disasters.

To determine the qualitative behavior of the function F ( x; k 1 , k ₂) , points parametrizable region I, just select any point of this region and explore the qualitative changes in the behavior of a function. Choose for ease of point ( k ₁, k ₂) = (+1, 0). Then the system (13) has only one real solution x = 0 and this solution determines the minimum.

d ³ F

Therefore, because of —— = 6 x = 0 all functions 8x³

parameterized control parameters of the region I, with only a minimum. Similarly defined qualitative behavior features parameterized points of the region III.

A convenient point for us in this field are ( k , k ₂) = ( - 1,0 ) : at this point the system (13) has three solutions – a local maximum at x =0 and two local minima at x =+ 1, x = - 1. Consequently, all functions parameterized area points III, should have two local minima and one local maximum.

As for features, parameterized points crease lines, in point 2 control parameters k 1 and k 2 have negative values. Along the left curve drafting local maximum and minimum should be left-sided degenerate. At the point A ₂ local maximum and minimum are right-degenerate. At the intersection of two fold lines at the point ( k , k ₂ ) = ( 0,0 ) and a maximum of two local minima corresponding function degenerate.

The function that describes the behavior of the system and has a degenerate stationary point by replacing the coordinates can be reduced to one of the elementary catastrophes [24-26]. For each function can be predicted from the region of stability and critical attitude parameters. It was established that the use of catastrophe theory to predict the behavior of the system in respect of control parameters.

If the target function of the control system depends on the three control parameters of the network: a – the

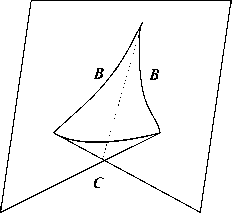
Fig.4. The surface of the catastrophe dovetail

We find a set of points R 3 in which the fourth order equation (15) has x triple root. We have:

^-F = 4 x ³ + 2 ax + bx = 0

. ^{5 x}                        .            (17)

3

^- = 12 x² + 2 a = 0

IS x³

Quadruple degenerate critical points are determined x = 0

a = 0 ' b = 0.

c = 0

This means that the function F ( x ,0,0,0 ) has a quadruple degenerate critical point x = 0. The lines connecting the points describing the behavior of a function with three degenerate critical points have the following parametric representation in the space of control parameters R ₃:

a = - 6 xx b = 8 x³ c = - 3 x⁴

Points that characterize functions with doubly degenerate critical points form a surface that in the space of parameters R 3 can be depicted as:

b = - 4 x ³ - 2 ax c = 3 x ⁴ + ax²

In a space R 3 with coordinates а , b , с with the discriminant of equation (15) defines a certain surface K . To describe the shape of this surface, we cross its planes а = const . Define a qualitative type of area, for this we consider any of its points, for example points 0, 2, 4 (Fig.5). Equation has a solution:

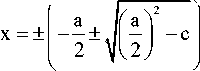
1/2

For a > 0: two real roots, if c < 0, and no real root, if c > 0; For a < 0: two real roots, if c< 0, four real roots, if 0 ≤ с < ( а /2)², no real solution if 0 <  с < ( а /2)².

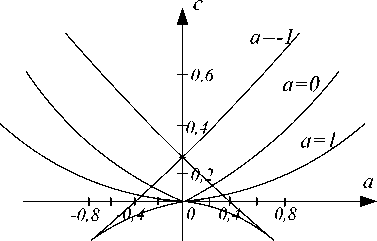
Fig.5. Cross-sections a = +1, a = 0, a = —1 catastrophe dovetail in space R3.

There are no critical points above the surface

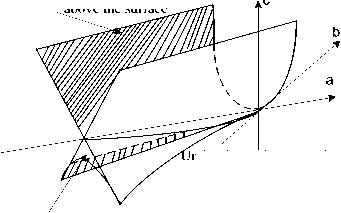
nder the surface 1 minimum, aximum

1 m

Inside the prism 2 minima and 2 maximums

Fig.6. Bifurcation areas of the catastrophe dovetail

As parameters pass across the surface of the regions, one minimum and one maximum of the target function disappears. In the bifurcation region with the point of turn, two minima and one maximum are replaced by one minimum; Behind them bifurcation type "roll" disappear. At the point of the swallowtail, two minima and two maxima occur in the same sense of the variable x. For values а > 0 there is either one pair (minimum, maximum) behind the swallow's tail, or there are no bifurcations at all. It depends on the values of the parameters b and c. Two surface bifurcations of the type "convolution" and two lines of bifurcation with the points of rotation occur at a < 0, and therefore disappear at the very point of the swallowtail, replacing one surface of the bifurcation type "convolution". Bifurcation regions are presented in Fig. 6.

The shaded part of the surface corresponds to an unstable position of equilibrium, while others are stable. In practice, if the delay grows despite the constant signal noise ratio, the system can fall into a state of disaster. By reducing the error probability and increasing the speed of information transmission, it is possible to compensate for the delay of the control signal.

The separatrix consists of points that characterize functions with two degenerate critical points and three surfaces describing functions with double degenerate critical points.

Thus, the set of points in which F ( x ; а , b , c ) has degenerate critical points divides the space of control parameters R 3 into three open areas. Any point R 3 can be approximated with a predefined accuracy of the sequence of points that lie entirely in one of these domains. This method allows you to predict the boundaries for the control parameters of the control system necessary for its stability. In the areas of stability, a combination with such methods of forecasting as statistical, extrapolation methods, and expert methods may be combined.

The disadvantage of the theory of disasters is that the prediction of system behavior with the number of parameters greater than 5 is not described, so predicting even a simple system is a complicated task.

It is shown that there are such values of parameters in the system, a slight variation of which leads to the breakup of the first kind of target function. The values of the parameters in which the maximum of the target function varies drastically, will be called the key values of the system parameters.

It is shown that a mathematical model, abruptly changes its behavior with a small change in its parameters and which can not physically be measured accurately, requires additional information.

Finding special parameters values in models represented by several thousand equations appears to be complex at first glance. The task is complicated by the fact that computational programs carry out numerical search of a decision only at specific points. However, the model changes its behavior not only in the point but also in a certain area, which allows numerical diagnostics, conducting step-by-step calculations in the vicinity of constraints.

The real control problem is actually much more complicated, since the equations describing the process are nonlinear. However, the criterion derived for linear systems can be used to study the stability in the general nonlinear case.

• IV. Conclusion

In the design of software-defined networking there is a need for new theoretical data on the assessment of its effective management. Theoretical and practical interest is the development of mathematical models to simulate the unusual (abnormal and extreme) situations related to management systems. In describing the objective function of mathematical tools used catastrophe theory, which allows you to analyze the stability of the system in respect of unexpected changes in the structure of the jumps and transitions.

It is shown that the number of indicators that characterize the quality of the real system can be very large. This means that the more quality parameters considered in the synthesis of the system, the more perfect will be synthesized system. At a time when more discounted quality indicators, while difficult to conduct synthesis without entering a relatively rough assumptions. Therefore, in practice there is an optimum number of quality indicators to be taken into account. Introduction of additional quality indicators does not lead to improvement, and the deterioration of the results of synthesis.

Determined that the function that describes the behavior of the system can be reduced to one basic and predict disasters outside the area of sustainability and related critical parameters.

The main regularities of the behavior of the optimal solution of the problem depending on the model parameters are investigated. It is shown that there are key values of parameters in which the target function has first-generation breaks. In this case, it is necessary to analyze the adequacy of the mathematical model. The algorithms of search of key parameters in systems of the big dimension are presented.

The use of methods of catastrophic theory for prediction of the behavior of SU is proposed at all stages of its life cycle, namely during periods of a jump-like change in the state of the system. The methods of this theory allow system parameters to change only in sufficiently limited boundaries. And these borders, in many cases, can be determined in advance, that is to predict. For disaster methods, the result of the forecast is the values that make it possible to navigate in the parameters of the emergency.