Optimization of secondary surveillance radar data processing

Published Online May 2019 in MECS DOI: 10.5815/ijisa.2019.05.01

The main information resources of the airspace control system include secondary surveillance radar (SSR) [1-5, 8, 15]. The SSR solves the following information problems [4]:

• •    determination of air objects coordinates;

• •    reception of flight information from the air object;

• •    transmission to the air object of the information, necessary for the flights monitoring and control, and the guidance of air objects;

• •    dispatching of air objects identification;

• •    radar identification of the national belonging of the detected air objects.

The SSR is a radar system used in the ATC, which not only detects and measures the position of aircraft but also requests additional information from the aircraft itself such as its identity and altitude. The SSR is based on the military identification friend or foe technology, and these two systems are still compatible today. This radar contains five different work modes (A, B, C, D, S). It should be noted that the frequencies of request and response signals in the SSR systems are 1030 and 1090 MHZ, respectively [9]. Imitative resistant (cryptographic) identification of air objects makes it possible to solve the problem of state affiliation and is an important condition for the functioning of a single information and communication space. Currently, the main identification method is the request-response communication mode implemented in the Identification Friend or Foe (IFF) systems [9-11]. It is a system that enables military, and national – civilian-located air traffic control (ATC) – surveillance systems to distinguish friendly aircraft, vehicles, or forces, and to determine their bearing and distance from the requester. The IFF is still in use by both military and civilian aircraft. Modes 1, 2, 3, 4 and 5 are for military use only. Mode 4 is an identification mode with encrypted pulses. It has 4 pulses for synchronization and 32 pulses with encrypted information. Mode 5 is similar to Mode 4 and it is a crypto-secure Mode but enhanced with an Aircraft Unique PIN.

To improve the quality of information services for consumers, the SSR signaling information is processed with extensive use of information technologies at the subsequent stages of data processing (primary, secondary, tertiary). This is because the complexity of the SSR data processing system does not allow for the formalization and analysis of its work as a whole. Therefore, as a rule, the data processing system is divided into parts [4-6], each of which performs certain calculations. However, such (existing) sequential processing of SSR data leads to the impossibility of implementing inter-stage optimization of data processing and, consequently, to a reduction the quality of consumers information support [7]

The use of multi-path airspace control information systems [16-19] allows to improve the quality of information support. However, the cited works also provide for staged data processing, which eliminates joint optimization of data processing and, as a result, reduces the quality of information support for decision makers.

In [20], the option of improving radar detection by adapting automatic dependent surveillance technology was considered, which is not enough to optimize the detection of an air object as a whole.

The work [21] is devoted to the improvement of data processing of requesting observation systems without taking into account inter-stage optimization of data processing.

This article discusses the joint optimization of signal data processing and primary processing of SSR data, which allows improving the quality of information support for consumers of the airspace control system.

The article is organized as follows: the tasks of processing SSR data and the introduction of an integral indicator of the quality of data processing, which allows combining the criteria for the efficiency of processing both signaling data and primary data processing based on adaptive control of the threshold for signal detection and it's discussed in section II. The synthesis of the optimal structure for detecting airborne SSR objects together with the detection of signaling data is presented in Section III. The results of the analysis of the optimal synthesized structure of the processing of signaling data and the primary processing of SSR data are presented in section IV.

In this paper, the structure of joint processing of signal and primary SSR data was synthesized for the first time, which made it possible to carry out inter-stage optimization of data processing and implement two variants for joint processing of signal data and primary data processing, which made it possible to improve the quality of information support for decision makers in the airspace control system.

• II.    Secondary Surveillance Radar Data Processing

The observation systems are the source of dynamic information about the air situation, their data serve as a basis for decision-making.

Data processing system of the surveillance systems is directly connected to the signal sources, it provides decision-making of the following tasks:

• •    detection of useful signals received from air objects;

• •    estimation of the received signals parameters;

• •    air objects detection;

• •    measurement of coordinates and parameters of air objects motion;

• •    obtaining of flight information from the airborne facility;

• •    identification of the air object based on the “friend

or foe” attribute;

The first two tasks (signal processing), as a rule, are performed by the signal processor [6], and the next four ones (primary data processing) are performed by the data processor.

The fifth and sixth tasks are solved by the SSR. This emphasizes the fact that the quality of the SSR information largely determines the quality of information support for the airspace control system.

It should be noted that the SSR always works in the presence of a significant intensity of intra-system noise [12]. The presence of intra-system noise, as well as the construction of the SSR transponder on the principle of a single-channel queuing system with failures [4,8,13], leads to the fact that the operational readiness factor of the aircraft transponder P is always less than one. The operational readiness coefficient is nothing more than the relative capacity of the aircraft transponder. The presence of intentional correlated noise in the SSR request channel can lead, as shown in [5,12], to complete paralysis of the respondents. The coordinate code or identification signals, representing several narrow-band signals and forming time-interval codes of ⁿ value are used as response signals, which determine the range to the airborne object.

One can use the probability of signals correct detection, defined as

D s = f [ q s P ,F = ^f ( z s ) = const ] ⁽¹⁾

for signal processing by private indicators of the quality of information support, where q – is the signal-to-noise ratio in the response channel, F – the is false alarm probability, z – is the analog threshold of signal detection.

The probability of an air object correct detection may be the quality indicator of information support for primary data processing:

d i = f ( D s ,z ) (2)

where z – is the digital threshold for detecting an air object.

Thus, when forming a decision the air object detection based on the output of the data primary processing meter, an estimate of the coordinate measurement vector a k is given, which is characterized by the correlation error matrix C ^{- 1} .

The mentioned above procedures make it possible to generate the air object form based on the SSR information, which includes:

& k ,C - ¹ ,PI ,"friend - or - foe" (3)

where PI - is the flight information, friend — or — foe" – is the air object identification.

When automatic formulating an air object, the criterion is the quality of the measurement of the coordinate information, through the probabilities of the actions, which include the following:

• •    probability of an air object detection;

• •    probability of correct flight information loss;

• •    probability of flight information distortion;

• •    probability of combining coordinate and flight information.

Let us briefly consider the given probabilities.

Without detecting an air object, it is not possible to realize reading of the flight information. As will be shown below, a joint optimization of signals and air objects detection makes it possible to improve the quality of air objects detection and, consequently, to improve the quality of information support for consumers.

When processing the flight information with the scheme by the criterion km , the probability of the correct flight information loss in the processing device can be written as

P p = i - p k,.                   (4)

where P – is the probability of the flight information output in the first m information responses.

When using the schemes of the flight information confirmation by the criterion k / m in the processing device, the probability of the flight information distortion will be:

m p^=Y CP (1 - рик) m - -          (5)

i=k where P – is the probability of the false flight information output.

The flight information can arrive with some delay with respect to the coordinate information. Then the number of a discrete unit of the flight information arrival will be:

N d = N d + T ( KI )/ r d              (6)

where N – is the number of a discrete unit of the flight information arrival; T(KI)  – is the delay for the secondary radar corresponding to the code KI; r – is the range discrete unit price.

Then the probability of combining the coordinate and flight information will be:

{ XT ' 1

N 0 Г             (7)

N 0 J where P 0  - is the conditional probability of arrival

I—Nо J of flight information in the gate from + Nd up to - Nd relative to the coordinate information of the air object. Consequently, the probability of combining the coordinate and flight information in the SSR is determined by the accuracy of measuring the coordinates of the air object.

Thus, the probability: p ^ = Dp_b can be the integral indicator of the quality of information support for the primary processing of data.

The usage of the proposed integral quality indicator allows us to combine the efficiency criteria for both signal processing and data primary processing based on the adaptive control of the signals detection threshold. Indeed, the optimality of the detection problem solution is determined, as a rule, by the Neumann-Pearson criterion, it is reduced to maximizing the probability of correct detection of signals and air objects with restrictions on the probability of a false detection.

Based on the obtained expression for the probability of consumer information support, it follows that improving the quality of information support for decision makers in an airspace monitoring system can be achieved by increasing the probability of detection or by improving the accuracy of estimating the coordinates of air objects. In the future, more attention will be paid to the first aspect.

• III.    Synthesis of the Optimal SSR Structure for Air Objects Detection

Let us perform a synthesis of the information support structure for consumers under different versions of the SSR signal data processing. Indeed, the use of timeinterval codes as response signals makes it possible to implement two schemes for detecting an air object:

• •    detection of response signals plus detection of an air object (I variant);

• •    detection of an air object by separate response signals plus detection of response signals (II variant).

Let us assume that the input of the consumer's data processing device receives decisions about the detection of signals from the SSR. Let us synthesize the structure of the air object detector using the incoming signaling data, taking into account that the response signals represent an interval-time code, i.e. they are formed by several narrow-band signals with a definite temporal arrangement.

In the SSR, the received signals are compared in the threshold device (TD) to the threshold after the optimum linear processing and detection. After the TD, implementations xt = 1 arrive for further processing, when in the time resolution element i = (1, M), according to the analyzed spatial resolution, threshold has been exceeded; when it did not happen, then xt = 0 . Thus, with the SSR , the customer is provided with a set of implementations x with the required quality of detection.

In this formulation of the task of detecting an air object, the observer has X = 1|х^|| implementations, where xy = 1, if the threshold has been exceeded in the time resolution element  [z = (1, M) j = (1, N)]

corresponding to the

considered spatial resolution; if not, - xy = 0 , N - is the number of signals in the packet.

A combination of zeros and ones x undergoes a joint processing at the signals level to make a decision on the detection of an air object. Obviously, it is a random variable x , that obeys the Bernoulli distribution:

MN

P ( X 11 ,..., X mn IH 1 ) = ПП P ( X ’ H 1 ) = i = 1 j = 1

a.,

=ППD?(1 - Dj) ’• i=1 j=1

Taking into account (10) and (11), expression (9) can be written as:

Л =

П П’ - j xj i=1  ’=1____________________________

MN

ППF '' -’x’ i=1   j =1

P ( x₄ ) = P " (1 — P ) 1 ^- x’             (8)

Taking the logarithm of (12), we obtain:

where P – is the probability of exceeding the threshold in the i -th time processing channel. P_y = F - is the probability of a false alarm in the absence of a signal, and P -/= Du — is the probability of detecting a signal when the signal is active.

Suppose that a set of the abovementioned random variables arrives to the input of the device for joint processing of the entire array of the received signals. Compatible probability distributions of all possible combinations of x both in the absence and in the presence of a signal (hypothesis H and H ), that is, P(x | H ) and P(x | H ) are arbitrary, but known. Let us form a likelihood ratio for each particular set:

L = ln Л  j ]^X’ (ln Dij - In Fij) + i=1 j=1                                      (13)

+ ( ^{1 - x}’ ) [ ^ln ( ^{1 -} D i’ )^{- ln} ( ^{1 -} F ij ) ] .

If we denote multipliers x :

^Qy = ^ln D y ^{- ln} F j ^{- ln} ( 1 ^- D y ) +

+

^ln ( 1 ^- Fj^ ^ln

D ’ ( 1 - F j ) ( 1 - D j ) F j

Л =

P ( x ij | H 1 )

P ( x ij | H 0 )

and reject the terms that do not depend on x , we get the optimal algorithm, by the Neumann-Pearson criterion, for detecting an air object by combining the preliminary solutions of all time processing channels:

Comparison Л with the threshold, determined from the permissible probability of a false alarm, provides an optimal decision on the presence or absence of a signal by the Neumann-Pearson criterion.

Through the independence of noise in the timeprocessing channels, one can write:

MN

P ( X _h,..., X mn IH о ) = ПП P ( X j H 0 ) = i = 1 j = 1

M N

= ПП F X ' C ¹ - F j ) ’ .

i = 1 j = 1

Independent events take place when thresholds are exceeded under the influence of a signal. Then we can write:

MN

L = EE Q ’ X ’ ^ z          (15)

i = 1 j = 1

where z - is the threshold, which is determined by the probability F (a false alarm of detecting an air object).

So, the joint processing of signals is reduced to the weighted summation of units and zeros x reflecting the previous decisions about the detection of signals received in the time processing channels. The weighting factors (14) increase the role of that time processing channel, where the probability D is higher and the probability F is lower. The foregoing allows us to depict the structure of the detector in the form shown in Fig.1.

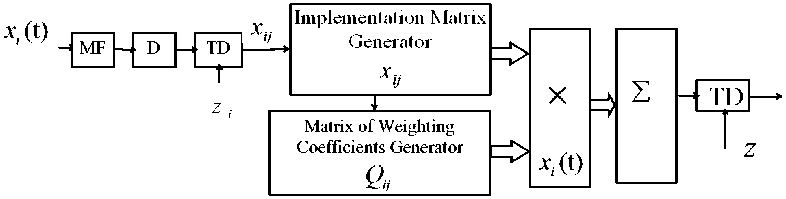
Fig.1. Structure of optimal air object detector

Two databases are formed based on the detection of signals in the primary data processing device: the first database contains the detection results in the elements of time and spatial separation, and the second one contains the weights of these detection results. To form weights, when making decision on the signal detection, the analog detection threshold value z , as well as the signal-to-noise ratio q , are supplied from the signal processing device. This separation of databases assumes both an optimal detection scheme algorithm (15), or a quasi-optimal scheme without taking into account the data processing weights.

Since x and x are 0 or 1, the left-hand side of (15) is the sum 1 <  M x N of the weighting coefficients Q .This means that it can take only certain discrete values. The threshold value z in this case can lie within the

MK limits 0 < z < ZZ Qj , so that, on the one hand, the i=1 j=1

trivial decision to detect an air object is not always taken, and on the other, a trivial decision not to detect an air object is taken.

With a fixed probability of previous solutions in the time and spatial processing channels F and D different decision rules give different values of probability F and D of the air object detection. However, these probabilities are determined by the weight coefficients Q , and, consequently, by the signals detection threshold and the signal-to-noise ratio. All this emphasizes the implementation of the joint optimization of signal processing and primary data processing.

With a fixed probability of previous solutions in the time and spatial processing channels F and D different decision rules give different values of probability F and D of the air object detection. However, these probabilities are determined by the weight coefficients Q , and, consequently, by the signals detection threshold and the signal-to-noise ratio. All this emphasizes the implementation of the joint optimization of signal processing and primary data processing.

It should be noted that the summation of the response signals in the processing channels is carried out without weights, through equal s/n ratios and the noise level in the channel, which simplifies the processing algorithm. Weightless summation of zeros and ones in the processing channels and replacement of the signalresponse detector with a decoder do not result in significant losses in the threshold s/n ratio.

It should be noted that the summation of the response signals in the processing channels is carried out without weights, through equal s/n ratios and the noise level in the channel, which simplifies the processing algorithm. Weightless summation of zeros and ones in the processing channels and replacement of the signalresponse detector with a decoder do not result in significant losses in the threshold s/n ratio.

The obtained algorithm (15) makes it possible to outline the structural diagrams of the detectors of air objects for the situations in question. There are three threshold devices in the synthesized detectors: the first one is a threshold device with an analog threshold, where the pulses of the response signals are detected, the second one is in the decoder (digital threshold) and the third one is used when an air object is detected (digital threshold).

The accumulation of data on the realizations and the corresponding weight coefficients in the databases makes it possible to implement both versions of data processing using information technology.

• IV.    Analysis of the Optimal Structure of Air Objects Detection

Let us carry out a study of the quality of air objects detection using a synthesized structure. The probability of detecting an air object is optimized by the joint optimization of signal detection and data primary processing in both versions of the SSR data processing. When calculating the probability of detecting an air object by the synthesized data processing structure, we will take into account the significance of the response signal code, which in practice is 2 or 3.

It should be noted in this case that the SSR data processing channel has an readiness factor for the aircraft transponder. The readiness factor of an aircraft's responder is nothing more than the relative throughput of an aircraft's responder [21].

Using expressions (14) and (15), it is possible to calculate the probabilities of detecting an air object for different values of the quantities z and the decisive rule. By selecting the analog signal detection threshold z with the appropriate rule for detecting an air object, the required probability of a false detection alarm at the output of the synthesized detector is ensured. All calculations induced below were obtained with F = 10 - 3 at the output of the synthesized air object detector.

Fig. 2 shows the dependencies of the probability of an air object detection D = f (q, n, P = 1) for both data processing methods (curves denoted by I for the first method, and II for the second method) with the timeinterval code values 2 and 3.

A comparative analysis of the dependencies presented in Fig. 2 shows, that the best quality indicators characterize the second data processing scheme. So, with q = 1.5 the probability of detecting an air object, using the first scheme, is 0.6, and using the second scheme it is 0.68 with n = 2 and 0.74 and 0.82 with n = 3 .

processing by the secondary radar. It is shown that an increase in the value of the time-interval code leads to a greater dependence on the availability factor of the aircraft transponder.

To study the effect of the aircraft's responder readiness factor to the quality of SSR data processing, we fix the SNR and calculate the probability of an air object detecting. Fig. 4 shows the dependencies of the probability of detecting an air object D = f ( P , n , q = 0.9) for both methods of data processing.

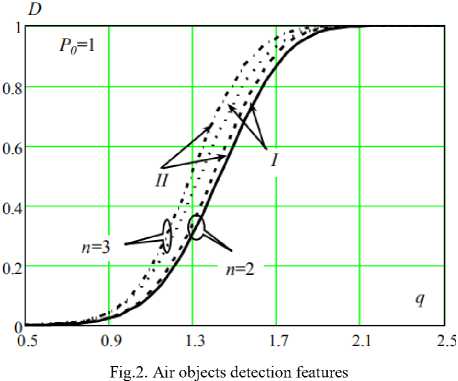
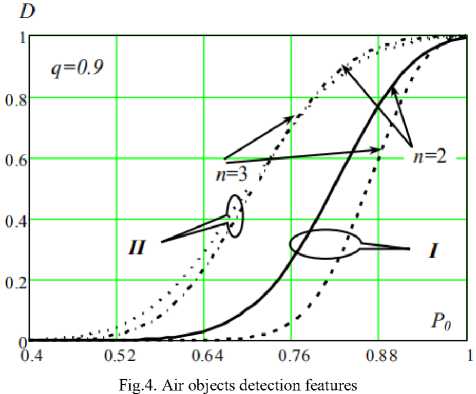
Fig. 3 shows the dependencies of the probability of AO (air object) detection D = f ( q , n , P = 0.9) for both data processing methods.

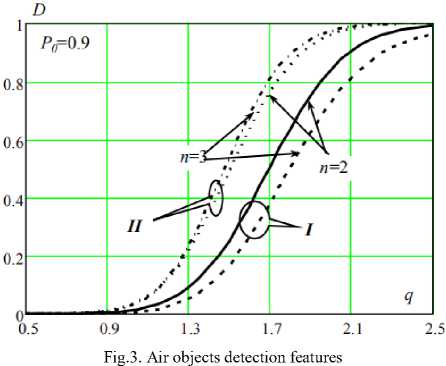
The calculations presented in Fig. 3 show the significant effect of the readiness factor of the SSR aircraft responder on the probability of detecting an air object by both data processing schemes. The second data processing scheme retains its advantages in comparison with the existing data processing variant in SSR. So with q = 1.7 the probability of detecting an air object using the first scheme is 0.5, and using the second scheme it is 0.78 with n = 2 and 0.39 and 0.8 with n = 3 . The presented dependences allow estimating the influence of the time-interval code value on the quality of data

The presented dependencies show that the second scheme is less sensitive to changes in the availability factor of the aircraft transponder.

• V.    Conclusion

In this paper, the secondary radar data processing structure is synthesized for the first time, whereby the signal processing and primary data processing are jointly optimized by taking into account the SNR and the signal detection threshold during the data primary processing stage.

The joint optimization of the detection of signals and airborne objects made it possible to implement an additional data processing scheme in which the detection of airborne objects occurs for each of the components of the response signal of the aircraft transponder.

Analysis of the synthesized data processing structure showed that the detection of an air object by separate response signals and the subsequent detection of response signals for the results of the detection of an air object have advantages in comparison with the existing structure of the primary processing of secondary radar data.