Optimized Angular a Star Algorithm for Global Path Search Based on Neighbor Node Evaluation

Published Online July 2014 in MECS

Programming a robot is a crucial part which involves lots of cost as well as time. Generally robots are programmed through one function but now days to avoid this overhead of programming robot for different functions it is much easier to write to build up robot semi-autonomous. This will reduce the overall cost and time of programming. It can be achieved by writing many algorithms with which robot can take the necessary actions. Algorithms like Dijkstra [1], A*[2] are useful for the same. Many scenarios are there in which robot has to work in unstructured and unpredictable environment. In these scenarios the robots are forced to face new situations for which decision making is quite difficult and moreover there is no pre-programmed motion, so at these difficult times robots have to take decisions to plan their motion. This Path planning [3] is quite difficult for robots due to several reasons. First, sensor based technique which is incomplete and inaccurate at certain times has to be used as preplan for motion. Second, there are many real-time constraints. Third, due to uncertainty in the environment, it is quite difficult to define the path. These challenges are exponentially growing with the increasing development in the domain of Robotics.

Early in the 1950s, the robots were only able to achieve the basic locomotion. Then moving ahead in 1970s and 80s, the optimal approach with different global objectives raised the research. Later, the picture came for real-time scenarios and constraints which focused on the overall cost of the planning and movement of the Robot. Initially, Robots were very much indoor and used in a controlled environment and then as the research progressed robots stepped into outdoor environment. Concentration was made for lesser and lesser prior information.

As discussed above path planning is an important task for robotics, so it is important to have a better algorithm for robot path planning and thereby finding a collision free motion from one position to another. These types of efficient algorithms [3] have important applications in areas like automated surveillance, industrial robotics, and drug design and computer animation. It is therefore not surprising that the research activity in this domain has been continuously increasing over the last couple of decades.

Robot path Planning is nothing, but just finding actions in sequence which helps in transforming some sort of the initial state into some desired ultimate goal state. Each transition has a cost associated to it. During the path planning all leading path from the initial point to the destination which the agent can take has their respective cost. Agent has to select a path whose combined cost is lesser than that of the other path. A good path planning algorithm should be having optimal path [4]. The centerpiece of this research work is to come up with an algorithm which can have combinational view of the distance as well as the angle from the Agent’s point of view to the destination point and can come up with the minimal cost for path planning. Another important point it should take care is that if the pre-planned path is not provided then in this case also the algorithm should be intelligent enough to decide dynamically [5] with respect to the environment about the minimum cost to reach the end point.

This paper proposes a better heuristic function for the A* algorithm as checked with the dataset in experiment. This algorithm will not be dependent on close set as like in A*. Here at every node robot advances one unit and the node to which robot proceed is decided base on the new heuristic function. This heuristic function not only decides the closeness of all the nodes to the goal node but due to the addition of an additional factor (angle to the destination) as discussed in the algorithm, it can also decide whether the given node is on the optimum path or not. This can easily be understood with the help of Fig-3 , in this we can see that the initial best approach path to the goal is along the line l, now suppose due to obstacle it can’t follow along the line l, so it will have to take an alternative path which means deciding on which node to proceed to among all the adjacent nodes, at this point it will calculate the distance for all the nodes and also add the additional factor ‘A’ (angular calculation), which basically measures the deviation of the new path from original optimum path. Example, say the ‘A’ in case of node 7 is less but the path is long so it will not be selected, this factor ‘A’ when added to the previous Heuristic Distance function gives new function which produces improved results over the previous functions. In this approach, local evaluation of node is done in contrast to algorithms like dijkstra, so it can be used for dynamic environment where the obstacles are moving and the path can be optimized as soon as robot acquires more knowledge, the path can be optimized[6]. There are some terminologies involved in this research work and it is represented in Table 1 below.

Table 1. Terms and their Definition

Terms	Definition
City block	Sum of absolute differences of ‘X’, ‘Y’ co-ordinates of any two nodes.
Grid	Matrix representation of the real world
Heuristic Function	The Function which returns desirability of each node.
Obstacle	Used in the matrix to simulate the real world obstructions.
STL	Standard template library in C++
Solution steps	All the nodes consisting of the robot traversal path.
Dataset	Information to be exchanged dynamically with respect to the topological behavior.

The paper is organized as follows. In section II, various techniques for simulating the real world environment has been discussed. In section III, detailed description of various path finding algorithm is presented. Proposed algorithm with data set is explained. In section IV, the implementation of the proposed algorithm is defined. In section V, result set is prepared and compared for the existing and the proposed approach. Finally, in section VI some conclusions are proposed and future scope of the work is discussed.

• II.    Environment Model

For an algorithm it is necessary to have an environment for the workplace. Basically environmental model is considered to be of two categories: grid based modelling and network/map based modelling methods.

Grid [7] based modelling is much simpler to implement like Quad-tree environment modelling algorithm and regular grid. Whereas the algorithms like Voronoi graph algorithm, MAKLINK graph algorithm, configuration space algorithm, etc. in Network/map modeling method are efficient in providing exact results, but the calculation cost is huge. This makes unsuitable for several applications. Taking into account of the cost effectiveness, grid method is used to for the representation of the robot work environment (Fig-1). The grid proportion is decided on the factor responsible for the work space and the size of robot. The obstacles are represented by numeric value ‘9’, for our experimental dataset. The grid is ensured that the robot can move in the grid. For the position of obstacles, we have ensured that they are well known before.

Fig. 1. Grid representation of the Map

• III.    Related Work

There are several approaches for the path planning of robot to the destination. First we will see the methods and renowned algorithms that have been discussed for path planning, and then we will go through the recent research applied in making the path planning more convenient for mobile robots. Path planning for the robots are mainly classified for partial known and unknown environments.

• A.    Dijkstra Algorithm

Dijkstra is an algorithm used for graph traversal and finding the shortest path of all the nodes from the starting node. Dijkstra works for graph having non-negative edge

Distance values. It produces shortest path tree from a particular source and can be used to find shortest path for a robot by representing the whole map as a graph and taking the starting position of the robot as source and destination as final node and then applying Dijkstra on this map formed. All the possible nodes can be represented as node in the graph.

How Dijkstra works is that, it starts with source and if the sum of the distance of the adjacent nodes of the sum is less than the sum of edge-cost (dist. (x, y)) and the sum to reach current node from the source. This process is repeated for all the nodes in the graph. The above process of repeating this process for all the nodes makes it inefficient, because if your destination is on the north side there is no logical explanation for considering the nodes on the south (if there are no obstacles present) but Dijkstra considers it which contributes to unnecessary processing of the nodes which are not fruitful or relevant to the path finding process, because of these shortcomings of Dijkstra a better algorithm based on the Dijkstra came into existence.

• B.    A* Algorithm

A* is an algorithm used in robotic path finding and for graph-traversal. It is like Breadth-first-search and does an exhaustive search of the graph and gives the least-cost-path from initial node to final node. A* selects the path of lowest weight using a priority queue.

Dijkstra considers the entire path adjacent to the current node even if they are not fruitful but A* uses a concept of Heuristic function to overpower this shortcoming of Dijkstra. Heuristic function can be understood in simple words as a function which tells the desirability of a particular function with respect to the process of path finding. What it means is that for a path planning exercise for a path from south to north. The nodes in path from south to node which hare north of current node are more desirable than nodes in east or west or south and hence are not considered for the path planning exercise.

In A*,the weight of each path is the sum of two costs one is the cost from the starting node to the current node and other is the heuristic distance which is a measure of desirability of each of the nodes adjacent to the node in consideration. It is better than Dijkstra because it chooses the next node which is more desirable (i.e a combination of both heuristic cost function and normal cost function). If for edge E(x, y) h(x) <= dist. (x, y)+h(y) (where dist.(x, y) is length of edge E(x, y) and h is the heuristic function), then the function h is called monotone function. A* is basically just an informed search which takes an informed decision while traversing the graph eliminating unreasonable choices which were considered in the Dijkstra so it is faster and efficient than Dijkstra. Several research works has been contributed in the same domain. Some of them are discussed below for the optimized path planning for mobile robots.

Dr. M.Jagadeeswari 2012 [8] in this paper the discussed algorithm involves the construction of the distance map initially for the image so as to obtain collision-free region, then the construction of the bfs tree of pixels in the collision-free region is done, this defines the shortest path from any start point to a specific goal or destination pixel. If multiple destinations are provided, the path is defined accordingly and traced to the nearest goal.

Song-Hiang Chia 2010 [9] presented the ant colony algorithm for the path planning of mobile robots. It focusses on the collision free area. Here the target searches for the collision free area by the ability of using ant colony algorithm. Using this algorithm the robot moves from start position i.e nest to the destination i.e food with in collision free area.

Adam A. Razavian 2005 [10] presented Cognitive Based Adaptive Path Planning Algorithm (CBAPPA) for Autonomous Robotic Vehicles. It evaluates the hypothesis that CBAPPA are efficient. The approach is based on based on cognitive based steps. Number of heuristic algorithms is implemented for each step. Functionally, CBAPPA checks for the optimal path in two stages i.e by finding primary path and then finding the refined path.

Linan Zu 2008 [11] this paper stated that the complexity for path planning can be debased by having a global path fist and then adjusting the local path according to inputs received dynamically. This local path planning can help the robot avoid both static and dynamic obstacle.

Zhou Weiteng 2013 [12] this paper reflects the variation of A* which uses the value of shared neighbors to find the solution for the path planning problem. It also discusses the approach of taking neighbors value in consideration for deciding the heading direction and the next node and can reversely search for the starting node from goal node using local evaluation rather than global evaluation.

Vanitha Aenugu and Peng-Yung[13] Woo presented the idea of finding robot path in an 3D environment where obstacles as well as goal node is moving randomly and the path to goal is not known in advance . They used 3D geometry concepts to generate path for the mobile robot in this randomly changing map. Because of ever changing map they had to use local evaluation techniques and can’t define a path for a robot initially. They introduced a concept of safety zone to avoid moving obstacles.

Fabio M. Marchese [14] in his paper “Multiple Mobile Robots Path-Planning with MCA” has proposed a collision free path for multiple robots from goal to final node considering the real size of robots.

• IV.    Implementation

Implementation for this proposed algorithm is done using C++ and winbgim.h (graphics library) has been used for graphics representation purpose. We have used STL which are available with C++ for data handling purpose. STL contains algorithms, iterators, functions and readymade classes of C++ such as containers and maps data structures. We have used maps data structure to store the coordinates of all the nodes and obstacles. By maintaining a Queue for all the nodes adjacent to current node we can select the node with the shortest distance.

The main idea is to have an initial map of the grid including the obstacles. Then with the help of sensors and discussed algorithm, the map could be updated as to find a global path [15], which is generated according to new input’s collected. Fig-2 shows the pictorial representation of the instance when robot have to plan the path considering the obstacles. The black node is the robot which has to reach the final node. Grid points are marked in yellow color throughout the grid. In Fig-3 Numerical value 9 is being used to denote the obstacles (In Implementation), which the robot has to avoid while planning the path.

• A.    Work Structure

  

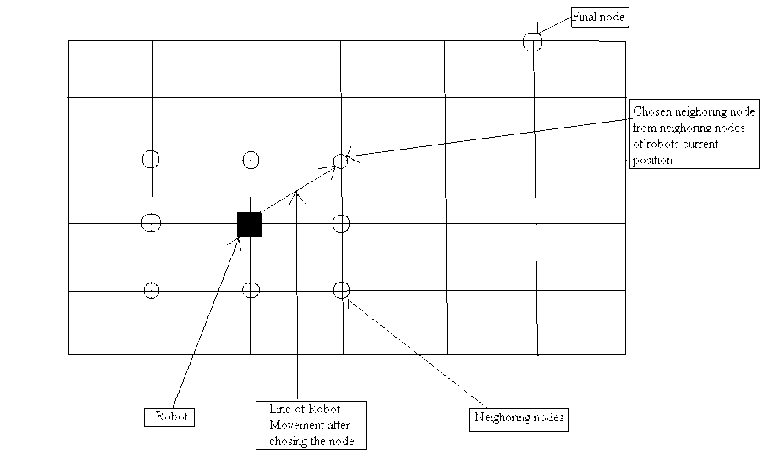
  Fig. 2. Representation of Node, Grid and the corresponding movement of robot

  
  

• B.    Experimental Data set

For the simulation of the algorithm, the grid of order 30 X 30 is taken. Black square is treated as robot. Yellow circles as represented by numerical value 1 are the grid points. Nodes represented by numerical value 9 are treated as the obstacles in the grid. In fig. 2 we have represented a scenario encountered by robot where it has eight neighbors as possible choices for next position to move to. It has to select one of these nodes, based on their desirability which is obtained by applying heuristic function.

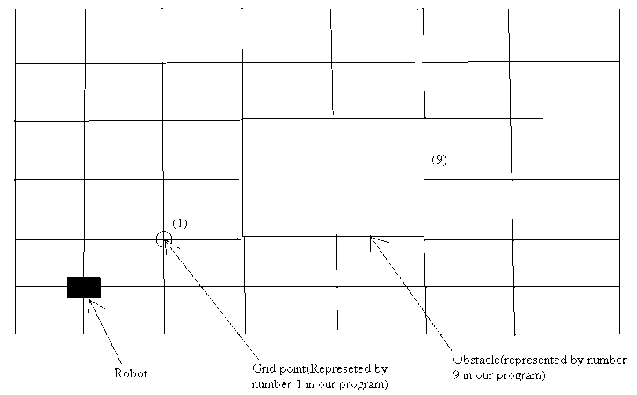
Fig. 3. Representation of Obstacle on map

• C.    Algorithm

The Algorithm is discussed below and its deduced results are in the next section of paper.

There are few constraints and values that are considered for this algorithm i.e.

• 1.    Robot is mobile and obstacles are in stationary position.

• 2.    The stimulation is done on the static grid map provided initially but this algorithm does not carry any restriction. It can work dynamically on the Grid map.

• 3.    The robot is of unit size.

• 4.    Robot can move on the GRID[16] by choosing next point from its neighboring 8 nodes(Fig-4).

Table 2. Showing the list of parameters used in algorithm with their description and values.

Parameters	Description
S’	Current node
S	Starting node
F	Destination
Dist. (S,D)	Distance between S and D
ANGLE(S',S,D)	Function returning the angle between initial lines of approach to the line of approach from the adjacent vertex.
EXTRACT-MIN(Q)	Function which return the minimum element from the queue and delete all other elements.
City Block	Distance (refer algorithm)
ATAN	Inverse of TAN (Arctangent)
D	Intermediate Node
Q	Queue holding the distance of all the nodes adjacent to the current node.

Let ‘S’ be the starting point and ‘F’ be the final point. Current node: =S

• 1.    for each vertex V adjacent to Current node.

• 2.    Add DIST (V, F) + ANGLE (Current node V, F) to a queue Q.

• 3.    If (Current node! = F)

• 4.    Repeat steps 1 to 4 for this node

• 5.    Else return

Current node=EXTRACT-MIN (Q)

DIST(S’, D): (this function returns the current node S’ from the node D)

• 1.    Calculate the distance between S(Xs’,Ys’) and D (Xd,Yd)

• 2.    If (city block)

• 3.    If (Euclidean)

City Block Distance=|Xs’-Xd|+|Ys’-Yd|

Euclidean dist. = (sqrt(pow((Xs’-Xd),2)+pow((Ys’-

Yd),2)))

ANGLE(S,S’,D): (Fig -4)

• 1.    Angle between lines from S(Xs,Ys) to final point(F(Xf,Yf)) from the initial vertex say S'(Xs',Ys') to F(Xf,Yf)

• 2.    Let m1 slope of line from s' to F:=(Yf-Ys')/(Xf-Xs')

• 3.    Let m2 slope of line from s to F:=(Yf-Ys)/(Xf-Xs)

• 4.    Return the acute angle between two lines

(Return ATAN((m1-m2)/(1+m1*m2)))

EXTRACT_MIN (Q)

• 1.    Sort the queue Q in ascending order

• 2.    Remove the first element in a variable say MIN

• 3.    Delete all the elements from the queue

• 4.    Return MIN

  angle between I & 11 (qi)

  shortest path between current & goal node (I)

  

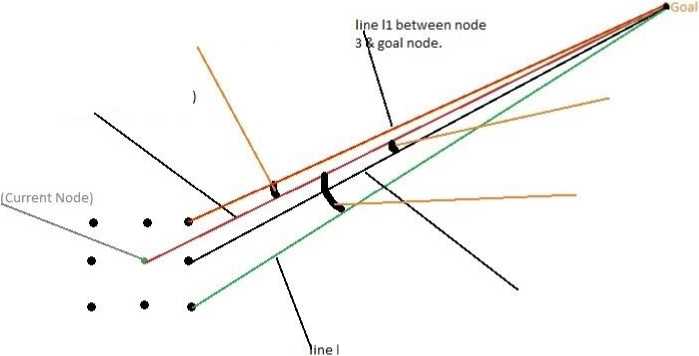
  Node

  angle between I & 12 (Q2)

  angle between I & 13 (Q3)

  13 between node

  line 12 between node

  4 & goal

  5 & goal

  Fig. 4. Inculcation of angular calculation from Current node in a grid to the destination node

  
  

• V.    Result and Discussion

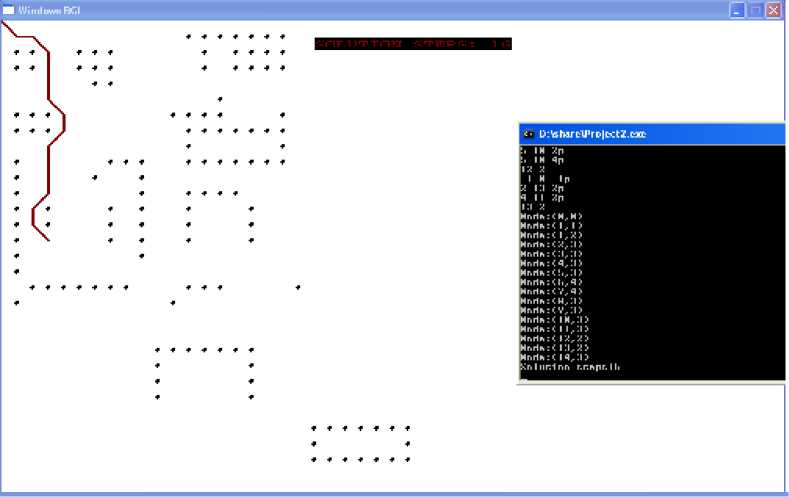
Fig. 5. Scenario (3) – Worst case scenario in which discussed algorithm gives the same path as of A star but never any longer path

Table 3. Statistical Data used in Experiment

Starting Co-ordinates	Destination Co-ordinates	Original Result (Solution Nodes)	Results with discussed approach
3,3	20,20	27	25
10,10	0,20	16	14
20,0	5,26	35	32
0,0	14,3	14*	14*

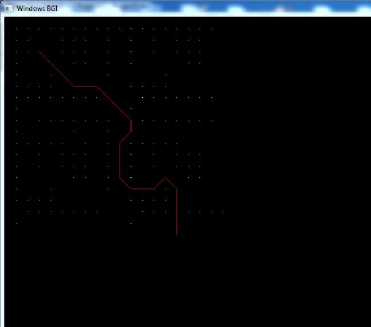
Fig. 6. Scenario (1): Traversal of Robot in a specified grid by using a star Algorithm.

* In the last step it proves that for the worst scenario if the algorithm does not improves then at the same time it does not deteriorate the result (Fig-5).

In Table 3, column 1 represents the starting position of the robot in respective grid and column 2 represents the destination or the goal node. Here the first value in the set represents the ‘X’ co-ordinate and second value represents the ‘Y’ co-ordinate.

Third column gives the number of intermediate nodes covered by the robot to reach to the destination using the previous approach. Column four gives the number of intermediate nodes using the proposed approach.

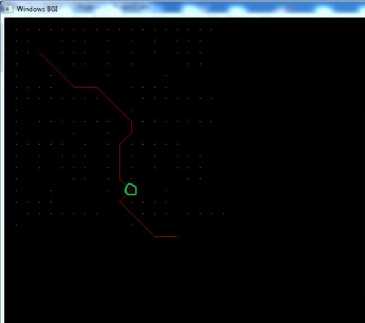
Fig. 7. Scenario (2): Path traversal using the modified algorithm.

• VI.    Conclusion and Future Scope of Work

One of the important parameters that results in the loss of energy in Robots, is the frequent turning and distance covered. The Simulation of the discussed algorithm shows that the energy waste can be reduced by keeping the robot more or less straight which reduces the number of turns robot has to take, even if the distance to target increases in some cases. Since we are dependent on neighboring nodes of the current nodes, the changing of the map does not much affect the algorithm only the nodes adjacent to current node affect the robots decision, since robot moves one step at a time. We can find the next node to move in the constant time. This saves the processing time.

Furthermore in future, explorations can be done on this area. Some other path planning and selection algorithm can be used that can select the most significant and optimized path with respect to time involved in it. In a heterogeneous environment where the number of robots is more than one there the individual robot should be able to exchange the dataset calculated over the dynamic environment with the same discussed algorithm. This will help to provide the robot with updated plan, to reach the Destination. It is synonymous to choke packets used in networking which gives router, information about any blocked path. Since a robot would have already calculated the best optimized path from its previous location to the destination. Thereby this path information can be also shared to the other robots which can prove useful to any other robot following the same path. Considering the time parameter the saved energy for calculation can have an impact over the performance and cost of overall system.

Conference on Artificial Intelligence, August 1995, Page(s):1625-1659.

We would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments.