Optimized Round Robin Scheduling Algorithm Using Dynamic Time Quantum Approach in Cloud Computing Environment

Published Online on February 8, 2023 by MECS Press

Cloud Computing (CC) is considered a highly beneficial technology in the modern IT world because of its accessibility, tremendous scalability, and incredible flexibility [1]. It is a sophisticated internet-based technology that deals with efficient maintenance of applications and proficient manipulation of data [2]. Moreover, it offers an inadequate number of technological services through a central remote server on the internet [3].

CC models have been categorized based on deployment and requirements named public, community, private, and hybrid cloud models [4]. Moreover, all CC models successfully provide plenty of computing services and resources [5]. The services and resources are infrastructural, platform, or hardware, and software-based [6]. In the field of CC environment, one of the crucial and decisive issues is Task Scheduling (TS) [7] as multitasking is one of the most considering and desirable requirements in this environment. The features about multitasking really enhance the performance of the cloud environment and increase the level of productivity. In addition, the multitasking environment manages the misplaced priorities efficiently in the cloud computing environment. The dynamic TS offers multitasking management significantly. Efficient task scheduling enhances the performance of a CC environment by contributing in the multitasking operations in terms of resources management [8].

There exist an enormous number of task scheduling algorithms such as First Come First Serve (FCFS), Shortest Job Fast (SJF), Longest Job First (LJF), Feedback Based Task Scheduling (FBTS), Priority-Based (PB), and Round Robin (RR) [9]. Some hybrid TS approaches are also available developed with two or more existing task scheduling algorithms [10]. All of those task scheduling algorithms have various considerable limitations depending on the scenarios. As for examples, FCFS offers a first come first serve manner, however, it is not comparatively suitable if a task with large burst time reaches into the ready queue firstly and a task with small burst time reaches into the ready queue lately or lastly because of being waiting for a large time for processing though the task has small burst time. In terms of SJF, the shortest job is executed first; however, the task having large burst times must have to wait for a long time before their completion. The longest job first executes the tasks which have the longest burst times. There is a problem which is similar to the FCFS. The problem is delaying a long time of having small burst times of the tasks into the ready queue. The feedback task scheduling utilizes the measurements of the execution and processing time along with sampling periods during taking decisions before assigning tasks for executions. The priority based scheduling has a great problem of starvation. It has no specific mechanisms or procedures for defining the priorities for the tasks for execution into the ready queue. Higher priorities and lower priorities are defined by the priority based scheduling algorithm. Priorities are determined based on the requirements of paging time, swapping time, execution time, access time into the resources, hold time of the resources, memory requirements and many other parameters. Higher priorities are received first and then the lower priorities those create starvation problems into the environment and system.

Among all of those existing TS algorithms, round-robin is outstanding and comparatively efficient [11] because of having a mechanism of determining dynamic Time Quantum (TQ). By defining or determining the TQ, each task is considered equally for each round and completes their execution based on the dynamically determined TQ successfully. The TQ whether can be fixed for each round or dynamically changed for each round. During defining static time quantum, the number of iterations can be more than adequate that means a large number of contexts switching. However, the number of context switching should be as minimum as possible based on expectation. From these concerns, the most significant feature that is determining TQ for each round should be dynamically that will understand the environment and surroundings of the ready queue, burst time of the tasks, and their arrival times for each round properly. The determination of the dynamic TQ is available now into the RR algorithm for TS. Moreover, there are also various modified, improved, and enhanced RR algorithms based on the determination of TQ [12]. It is undoubtedly a vital term that enhances the performance of a round-robin task scheduling approach along with the cloud computing environment with manifolds [13].

This paper introduces a New Round-Robin Task Scheduling Algorithm (NRRTSA) for the cloud computing environment with the determination of a comparatively efficient time quantum dynamically and instantly. In the NRRTSA, the determination of the TQ has been done by understanding the environment and surroundings of the ready queue, burst time of the tasks, and their arrival times. The proposed NRRTSA has been developed with a dynamic TQ determination mechanism that enhances the performance of resource distributions from the central remote servers in the cloud computing environment. The staple contribution is that the efficient dynamic time quantum for the proposed approach has been determined dynamically and instantly by considering differences among three maximum burst times of tasks in the ready queue for each round. The determination also performs additive manners for reducing algorithmic complexities. In addition, the proposed approach has been comparatively efficient and optimal in terms of minimizing average turn-around time, average waiting time, and number of contexts switching during scheduling the processes. The proposed NRRTSA belongs to determining the dynamic attitude in terms of determining its operational time quantum for each round. At determination, it focuses on the availability of tasks into the ready queue in the cloud computing environment. Three maximum burst times are picked for determining the time quantum for each round. A few differences among the maximum burst time based tasks have been determined and eventually an additive manner has been utilized for finally determining the dynamic time quantum for each round at the proposed strategy NRRTSA. At each round, the time quantum is being determined by considering the number of tasks needed to be served into the ready queue. It can be the presence of a single task, a couple of tasks, and more than a couple.

The entire methodology has been described and pictorially demonstrated in the proposed methodology section. All distinct procedures involved in the proposed NRRTSA have been accomplished and applied on various datasets. The datasets are having large number of tasks, small number of tasks, ascending order oriented burst times based large or small number of tasks, descending order oriented burst times based large or small number of tasks, tasks having same arrival times, tasks having different arrival times and various prominent combinations among number of tasks, arrival times, burst times of the tasks. Having considered all the datasets, the proposed NRRTSA provides excellent results comparatively. The number of contexts switching, average turn-around time for all datasets, average waiting time for all datasets is really optimal and considerable. The experimental results demonstrate that the proposed NRRTSA has enhanced the performance of the round-robin task scheduling algorithm in the cloud computing environment by reducing Average-Turn-Around-Time (ATAT), Average-Waiting-Time (AWAT), and the Number of ContextSwitching (NCS) with better accuracy. Another improvement is that the allocation of resources in the cloud computing environment has been optimized and comparatively best utilization because the number of context switching has been minimum for each context. In addition, the tasks need not to do more waiting for receiving their desired resources from the cloud computing environment during their execution. More specifically, the average turn-around time has been dramatically reduced that enhances the performance during execution. All of those ensure the best utilization of resources for the available tasks needed to serve in the cloud computing environment which is comparatively desirable. Eventually, the comparison between NRRTSA and other existing round-robin approaches shows that the proposed NRRTSA is comparatively better, acceptable, and optimal.

The rest of the paper has been consecutively organized as follows: Section two describes the related work from the existing literature on round robin algorithm. Several existing problems on this algorithm have been figured out and critical judgments also presented. In section three, the proposed round robin algorithm has been portrayed with flowcharts and algorithms. Experimental result and discussion have been demonstrated on different datasets on section five and a comparative study has also been presented on this section. Finally, the conclusion and future research direction on this research is presented in section six.

2.    Literature Review

Cloud computing environment has been extensively utilized in modern sophisticated IT world. In terms of distributing resources from a remote server in the cloud computing environment, task scheduling enhances the effectiveness of a cloud computing environment specially. Round Robin is the most considerable algorithm that is highly suitable for scheduling tasks in a cloud computing environment related to allocation of resources from the remote server [14]. RR is totally free from starvation problem like priority based approach and it reduces worst case response time. It ensures a fair allocation of the tasks or jobs during allocating resources, or executing tasks into the waiting queue to ready queue. Round robin offers a crucial term called time quantum that executes all the tasks equally at a simultaneous time. This time quantum for the RR can be statically defined or can be dynamically defined during execution of the tasks into the ready queue.

Nowadays, Sundry TQ determination approaches are available in terms of increasing the performance of the RR algorithm. Some scholars utilized maximum burst times, mean of the burst times, median of the burst times, differences among available burst times into the ready queue, hybrid combination of prioritization and round robin mechanism to determine the TQ for the RR method. However, RR follows a cyclic way and the preemptive approach of the RR turns into the first come first serve manner. Since it depends on time sharing, number of contexts switching often gets high due to worst determination of TQ. In addition, the average turn-around time and average waiting time also get high. The literature review section has explained some existing popular round robin task scheduling algorithms involved in the cloud computing environment. Methods, approaches, performance, and limitations of each round robin task scheduling algorithm (RRTSA) have been described and criticized in the following.

Fataniya Bhavin et al. [15] developed a hybrid RRTSA with the existing SRBRR [16] and MRRA [17] algorithms. The approach reduced ATAT, AWAT, and NCS for various premeditated datasets. However, the outcomes of DQRRR would not be efficient if the differences among burst times became very high or low or almost equal during determining its time quantum. Verma Rishi et al. [18] considered a large and a small burst time. A difference had been calculated to design a RRTSA. The method also performed well for various premeditated datasets. However, the outcomes would not be efficient if the difference became very small. Biswas Dipto et al. [19] introduced a RRTSA by considering the maximum difference and a median value among all sorted burst times of tasks in ready queue. The PRR strategy reduced ATAT, AWAT and NCS for many datasets. The outcomes would not be proficient if the difference became very small among all burst times of tasks in ready queue. Pradhan Pandaba et al. [20] developed a RRTSA depending on an average value of all burst times present in the ready queue during determining the time quantum. The approach utilized quick sort approach that caused higher cost and generated less beneficial outcomes if the average became equal to the median value or almost equal to the median value after sorting.

Behera Patwari et al. [21] introduced another RRTSA by measuring and considering priority. The PBDRR method performed well for many datasets but caused starvation. In PBDRR approach, the tasks had been separated as shorter burst times and longer burst times. However, the way of prioritization for tasks had not been expressed explicitly. Matarneh Rami J. et al. [22] proposed a RRTSA considering self adjustment approach among different burst times during determining the time quantum. The SARR strategy specifically considered a median value and a specific value that is 25 for self adjustment in terms of determining the time quantum. Sunny Mittal et al. [23] designed a RRTSA by determining and considering a median value. The median value had been calculated without sorting. The SRBRR approach reduced ATAT, AWAT, and NCS for various datasets. However, the outcomes of SRBRR would not be proficient if the median value became very small. Even, the SRBRR would behave like a FCFS scheduling algorithm if the median value became equal to the maximum burst time or greater than the maximum burst time in the ready queue during determining the time quantum.

All of the above existing round robin task scheduling approaches performed well for various premeditated datasets. Moreover, there are an enormous number of datasets for which all of the existing RRTSA increased ATAT, AWAT, and NCS at a higher rate. This increment of the ATAT, AWAT, and NCS decrease the performance and effectiveness of a cloud computing environment. This research has proposed a NRRTSA that overcomes all of these challenges mentioned in the above existing approaches and performed comparatively very well for all types of datasets. The experimental results demonstrate that the NRRTSA reduced the ATAT, AWAT, and NCS for various types of datasets. The comparison shows that the proposed NRRTSA is comparatively optimal and enhances the performance of the task scheduling for building an effective cloud computing environment.

3.    Proposed Dynamic Round Robin Approach

This section has explained all the procedures and strategical functionalities of the proposed new round-robin task scheduling algorithm. The proposed NRRTSA has been pictorially depicted in the Fig. 1. All tasks T i are inputted in the Ready Queue (RQ) considering their arrival times (AT i ). Sorting is the first approach to arrange all the T i based on their burst times (BT i ). The proposed NRRTSA has utilized heap sorting approach [23] to overcome sorting complexities along with sorting time complexities. After wards, the efficient Time Quantum (TQ) for the proposed NRRTSA has been determined by considering the number of tasks in RQ and their burst times. The process of determining the efficient time quantum for the proposed NRRTSA has been sequentially described in the algorithm 2.

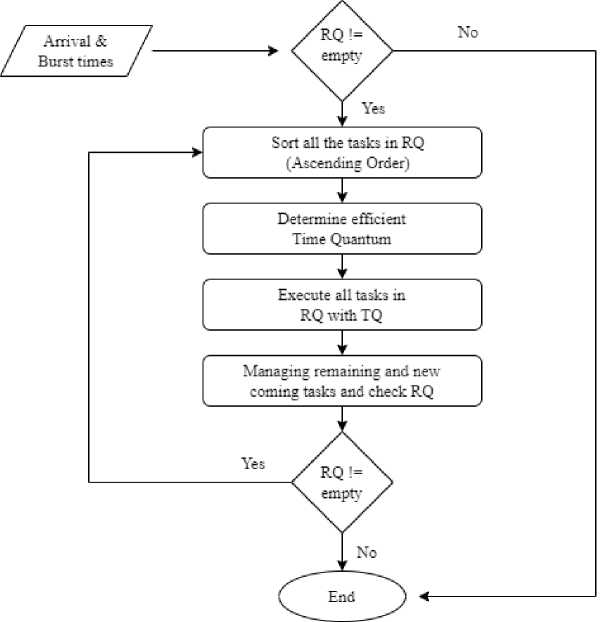
Fig.1. Procedure of the Proposed NRRTSA.

The proposed NRRTSA approach has utilized four distinct equations during determining the efficient time quantum for optimal task scheduling. The equations are as follows.

D1 = BTMAX1 – BTMAX2

D2 = BTMAX1 – BTMAX3

TQ = ((D1 + D2 + BTMAX2 + BTMAX3) ∕ 2) - 1(3)

TQ = (D1 + BTMAX1 + BTMAX2) ∕ 2(4)

All of those four equations have been utilized during determining the efficient time quantum for the proposed NRRTSA. Here, D 1 and D 2 are two differences among three maximum sorted burst times of the tasks in the ready queue. Eventually, the efficient time quantum has been determined by following a simple additive method. There are two distinct equations for the time quantum. One of the equations has been utilized during determining the efficient time quantum for the proposed NRRTSA based on considering the current number of tasks in the ready queue. The optimized and dynamic TQ determination process for the proposed NRRTSA has been depicted in Fig 2. After determining the efficient time quantum, each task in the RQ has been executed sequentially by considering the efficient TQ. The unfinished tasks and new arrived tasks have also been submitted to the ready queue for further execution. A new efficient time quantum is determined again dynamically and instantly for those existing tasks awaited in the ready queue. Like this, an optional, and efficient TQ is determined dynamically and instantly for the existing tasks in the ready queue for each round. Eventually, the execution becomes end when the ready queue becomes empty. The execution process has been sequentially described in the algorithm 1 and the TQ determination process for the proposed NRRTSA has been described in the Algorithm 2.

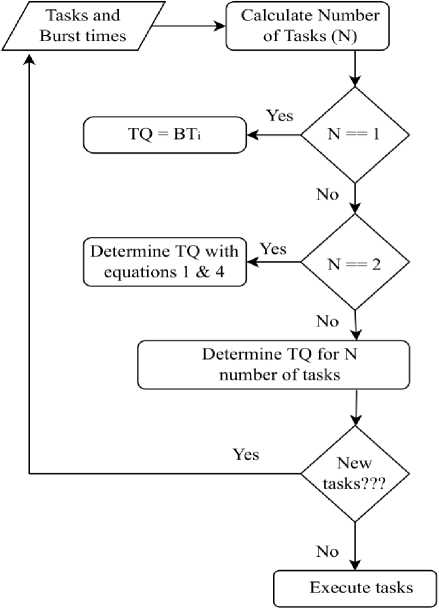
Fig.2. Dynamic Time Quantum Determination Process for the Proposed NRRTSA.

According to the proposed methodology of the proposed NRRTSA, all the tasks in the ready queue have been executed by the efficient dynamic time quantum successfully. The proposed NRRTSA has been applied on four distinct datasets to measure its performance in terms of task scheduling for the cloud computing environment. The experimental results demonstrate that the proposed NRRTSA has reduced ATAT, AWAT, and NCS with a higher rate and optimal accuracy for all the datasets. As well as, the comparison with other existing round-robin task scheduling approaches shows that the proposed NRRTSA is comparatively better, acceptable, accurate, and optimal for scheduling tasks in a cloud computing environment.

4.    Experimental Results

This section has sequentially consisted of four subsections named Datasets Collection, Measurement Matrices, Experimental Results, and Discussion. All the subsections have been elaborately explained in the following.

• 4.1.    Measurement Metrics

This subsection has described all the required and utilized measurement matrices. With a view to measuring the performance of the proposed NRRTSA, three parameters have been considered as the measurement matrices such as average-turn-around-time (ATAT), number-of-context-switching (NCS), and average-waiting-time (AWAT). The ATAT indicates an average time that is utilized to complete the requests of all tasks for any resources. The AWAT also indicates an average time that is required to get responses on the requests for any resources generated by all the tasks. The NCS is a number that specifies the number of movements from one task to another task in order to fulfill the requests for resources based on the time quantum. Equations for the ATAT and the AWAT are –

Algorithm 1: Execution Process of the Proposed NRRTSA

Input: Arrival Times (AT 1 , AT 2 , AT 3 ……. AT n )

Burst Times (BT 1 , BT 2 , BT 3 ………..BT n )

Number of tasks and Tasks (T 1 , T 2 , T 3 ……. T n )

Output: Average turn-around time, average waiting time, number of context switching.

• 1:    Assign all tasks into the ready queue based on the Arrival Times

• 2:    while (RQ != empty) do

• 3:       Sort all tasks in ascending order.

• 4:      Determine time quantum based on the Algorithm 2.

• 5:      for each task T i in RQ do

• 6:               Execute T i

• 7:             BT i = BT i – TQ

• 8:          if BT i < TQ do

• 9:                        Execute T i again.

• 10:              End if

• 11:              Else

• 12:                        Put T i into the RQ again.

• 13:              End else

• 14:              if BT i == 0

• 15:                      Remove the T i from the RQ

• 16:              End if

• 17:      End for

• 18:       if New T i arrives do

• 19:             Assign into the RQ

• 20:             Go to step 2

• 21:      End if

• 22:    Go to step 2

• 23:    End while

• 24:    End

Algorithm 2: Dynamic TQ determination Process for the Proposed NRRTSA

Input: Burst Times (BT 1 , BT 2 , BT 3 ………..BT n )

Number of tasks and Tasks (T 1 , T 2 , T 3 ……. T n )

Output: Time Quantum (TQ).

1: Begin

2: Calculate number of tasks (n) into the RQ.

3: if n == 1 do

4:               TQ = BT i of that task.

5: else if n == 2 do

6:	Determine 2 Max BT i in the RQ.
7:	Max 1 = nth BT i
8:	Max 2 = (n - 1)th BT i
9:	Determine D 1 based on equation 1.
10:	Determine TQ based on equation 4.
11:	Return TQ
12:    End else 13:      else do 14:	Determine 3 Max BT i in the RQ
15:	Max 1 = nth BT i
16:	Max 2 = (n – 1)th BT i
17:	Max 3 = (n – 2)th BT i
18:	Determine D 1 based on equation 1.
19:	Determine D 2 based on equation 2.
20:	Determine TQ based on equation 3.
21:	Return TQ

22: End else

23: End

ATAT = ∑(FT i - AT i ) ∕ N                                     (5)

AWAT = ∑(TAT i – BT i ) ∕ N                                  (6)

The ATAT is an average of the differences between finished times of all tasks (FT i ) and arrival times of those tasks (AT i ). Similarly, the AWAT is another average of the differences between turn-around times of all tasks (TAT i ) and burst times of those tasks (BT i ), and N is total number of tasks into the ready queue during execution.

• 4.2.    Datasets

• 4.3.    Experimental Results

This subsection has introduced all 4 datasets on which the proposed dynamic round robin task scheduling approach has been applied to measure its performance. Among those 4 datasets, there are 2 existing datasets and 2 own created datasets depicted in the Table 1. Each dataset consists of five tasks. The table 1 contains all of the 4 datasets with their tasks, arrival times of that tasks, and burst times of all tasks.

Table 1. Four Distinct Datasets for Experiment and Comparison

Datasets	Tasks (T i ) with their Arrival Times (AT i ) and Burst Times (BT i )
Dataset 1 [19]	Tasks	T 1	T 2	T 3	T 4	T 5
	AT i	0	0	0	0	0
	BT i	105	85	55	43	35
Dataset 2 [19]	Tasks	T 1	T 2	T 3	T 4	T 5
	AT i	0	2	4	8	16
	BT i	95	75	60	43	26
Dataset 3	Tasks	T 1	T 2	T 3	T 4	T 5
	AT i	0	0	0	0	0
	BT i	165	206	25	92	333
Dataset 4	Tasks	T 1	T 2	T 3	T 4	T 5
	AT i	1	2	3	4	5
	BT i	9	12	3	4	19

In the Table 1, for each dataset there are 3 parameters such as arrival time (AT i ), burst time (BT i ), and number of tasks. For the first dataset, the burst times are in descending order with arrival times zero. For the second dataset, the arrival times are different and burst times are not in any order. In the second and third datasets the burst times are very high in value. The fourth dataset consists of 5 processes with low value based burst times. The entire methodology has been described and pictorially demonstrated in the proposed methodology section. All distinct procedures involved in the proposed NRRTSA have been accomplished and applied on various datasets. The datasets are having large number of tasks, small number of tasks, ascending order oriented burst times based large or small number of tasks, descending order oriented burst times based large or small number of tasks, tasks having same arrival times, tasks having different arrival times and various prominent combinations among number of tasks, arrival times, burst times of the tasks.

The experimental results subsection has mathematically explained the overall procedure of the proposed NRRTSA explicitly with another 2 distinct own created test cases. This demonstration has clearly clarified the determination process of the efficient time quantum for the proposed NRRTSA and the execution process of all tasks through the proposed NRRTSA with the determined efficient TQ. The preliminary experiment was conducted into an intel core-i7 processor, 16 GB RAM, and 4GB Nvidia 920mx GPU. The proposed algorithm has been implemented in both C++ and python programming languages and run into the jupyter notebook kernel, linux and all versions of windows operating systems successfully. A test case has been chosen for experiment containing 7 tasks such as T1, T2, T3, T4, T5, T6, and T7 respectively. The arrival times of all tasks are zero. The burst times of all tasks are 9, 12, 5, 10, 2, 11, 17 respectively. The considered arrival times for all tasks are zero.

T5

тз

Т1

Т4

Тб

Т2

Т7

Т7

О 2         7       16      26      37      49      65       66

•<-------------------► TQ = 16 •<-----------------------► TQ = 1

• Fig.3.    Gantt Chart for the Test Case 1.

Based on the proposed NRRTSA, all tasks have reached in the RQ at a time. After sorting, the sorted burst times of all tasks are 2, 5, 9, 10, 11, 12, 17. Based on the sorting the tasks are arranged in the RQ like T5, T3, T1, T4, T6, T2, and T7, here, the number of tasks in the RQ is more than 2. Three maximum burst times are Max1 = 17, Max2 = 12, and Max3 = 11. Based on the equations 1, 2, and 3, D1 = 17 - 12 = 5, D2 = 17 - 11 = 6, and TQ = (5+6+12+11)/2 - 1 = 16. After first round, there remains only 1 task in the RQ. So, new TQ for the second round is TQ = 1. After execution of all tasks, with the determined efficient TQ have been depicted by a Gantt Chart in the Fig. 3.

Based on the Gantt Chart in the Fig. 3, the turn-around times of all tasks are 16, 49, 7, 26, 2, 37, 66. Similarly, the waiting times of all tasks are 7, 37, 2, 16, 0, 26, 49. Eventually, the ATAT is = (203 / 7) = 29, the AWAT is = (137 / 7) = 19.57, and the NCS is = 8.

Another test case has been chosen for experiment containing five tasks such as T1, T2, T3, T4, and T5. The arrival times of all tasks are 0, 0, 2, 3, 5. The burst times of all tasks are 21, 19, 5, 15, 23 respectively. Based on the proposed NRRTSA, T1 and T2 tasks are in the RQ firstly. The sorted burst times of the tasks are 19, 21. Here, the number of tasks is 2. So, Max 1 = 21 and Max 2 = 19. Based on the equations 1 and 4, D 1 = 21 - 19 = 2, TQ = (2+19+21)/2 = 21. Those two tasks are executed. After that, all remaining tasks are in the RQ. The sorted burst times are 5, 15, 23. Here, the number of tasks is more than 2. So, Max 1 = 23, Max 2 = 15, and Max 3 = 5. Based on the equations 1, 2 and 3, D 1 = 23 - 15 = 8, D 2 = 23 - 5 = 18, TQ = (8+18+5+15)/2 - 1 = 46/2 - 1 = 23 - 1 = 22. The TQ for the first and second rounds are 21 and 22. After second round, T5 is remaining in the RQ to be executed. For the third round, the TQ is 1. After the execution of all tasks have been depicted by a Gantt Chart in the Fig. 4.

T2

T1

T3

T4

T5

T5

О 19      40      45      60      82      83

TQ = 21             >TQ = 22<---- TQ = 1

• Fig.4.    Gantt Chart for Test Case 2.

5.    Result Evaluation and Discussion

Based on the Gantt Chart in the Fig. 4, the turn-around times of all tasks are 40, 19, 43, 57, 78. Similarly, the waiting times of all tasks are 19, 0, 38, 42, 55. Eventually, the ATAT is = (237 / 5) = 47.4, the AWAT is = (154 / 5) = 30.8, and the NCS is = 6. The proposed NRRTSA has been successfully accomplished and has been suitable for any kind of test cases at any volume. The proposed NRRTSA has been examined with more than 5000 own created test cases, and more than 50 existing datasets. The proposed NRRTSA has reduced ATAT, AWAT, and NCS with an outstanding rate comparatively than other existing RRTSAs demonstrated in the Discussion and Evaluation subsection.

This discussion and evaluation subsection has discussed various challenges eradicated by the proposed NRRTSA, evaluated the performance of the proposed NRRTSA by a comparison with other existing RRTSAs, and introduced the limitations of the proposed NRRTSA. The proposed NRRTSA has eradicated the starvation challenges during scheduling tasks and ensured a legitimate distribution of resources for each task. The proposed NRRTSA has confirmed the determination of an efficient TQ that has provided comparatively outstanding performance for any kind of test cases and datasets. A comparison has been performed among the proposed NRRTSA and 7 others existing RRTSAs by utilizing 4 distinct datasets mentioned in the Datasets Collection subsection. The numerical results of comparison has been recorded in the Table 2.

The Table 2 contains 8 approaches in total with the results of comparisons among all of them for all distinct datasets. For each approach, there are 3 rows in the Table 2. Those rows contain the values of NCS, ATAT, and AWAT respectively for each dataset. Moreover, the comparisons have been graphically represented in the Fig. 5, Fig. 6, Fig. 7, and Fig. 8 respectively. The Table 2 shows that the proposed dynamic round robin task scheduling approach has provided very considering consequences for all times of datasets. The comparison demonstrates that the proposed NRRTSA has reduced the ATAT, AWAT, and NCS with a better rate than other existing popular round robin task scheduling approaches. Eventually, it has been made explicit that the proposed NRRTSA is suitable, optimal and efficient in task scheduling action in terms of resource allocation fairly in a cloud computing environment. There exists some staple limitations such as the proposed NRRTSA is not capable of increasing comprehension, determining priorities for tasks available in a cloud computing environment, and providing any prominent priorities for any highly momentous tasks.

The Fig 5 has demonstrated comparison regarding average turnaround time and average waiting time mentioned as ATAT and AWAT at Y-axis and legend. The values for this comparison have been received and observed from the table 2 for the dataset 1. Regarding ATAT, the last mentioned scattered point is for the proposed NRRTSA which smartly represents that the proposed method yields comparatively less average turnaround time for the dataset 1. In addition to, concerning the AWAT, the last mentioned scattered point is also for the proposed NRRTSA which explicitly represents that the proposed method suffers comparatively less average waiting time for the dataset 1.

The Fig 6 has also demonstrated comparison regarding average turn around time and average waiting time mentioned as ATAT and AWAT at Y-axis and legends. The values for this comparison have been received and observed from the table 2 for the dataset 2. Regarding ATAT, the last mentioned scattered point is for the proposed

NRRTSA which smartly represents that the proposed method yields comparatively less average turn around time for the dataset 2. In addition to, concerning the AWAT, the last mentioned scattered point is also for the proposed NRRTSA which explicitly represents that the proposed method suffers comparatively less average waiting time for the dataset 2.

Table 2. Results of Comparison among Proposed NRRTSA and Other RRTSAs for All Datasets.

All Approaches	Result of Comparisons over 4 distinct datasets
	Metrics	Dataset 1	Dataset 2	Dataset 3	Dataset 4
DQRRR [12]	NCS	8	8	9	10
	ATAT	209.4	198.2	402.6	32.4
	AWAT	144.8	138.4	210.4	17
SARR [15]	NCS	8	8	9	9
	ATAT	250.4	232.2	450.6	42.8
	AWAT	185.8	172.4	250.4	25.2
MRRA [18]	NCS	15	11	12	10
	ATAT	206.6	193.8	405.6	32.4
	AWAT	142	133.8	213.7	19.4
PRR [19]	NCS	7	8	9	12
	ATAT	169.4	185.2	370.6	25.4
	AWAT	99.8	125.8	199.5	16.2
MRR [21]	NCS	8	8	9	8
	ATAT	171.4	184.4	420.6	29.4
	AWAT	106.8	129.6	249.2	21.2
PBDRR [22]	NCS	12	9	11	10
	ATAT	289.4	256.8	449.2	42.8
	AWAT	224.8	197	282.4	22
SRBRR [23]	NCS	8	8	10	10
	ATAT	170.2	184.8	439.6	39.4
	AWAT	105.6	125.6	211.4	29.6
Proposed NRRTSA	NCS	6	6	6	6
	ATAT	157.4	174.6	346.6	19.4
	AWAT	92.8	114.8	182.4	10

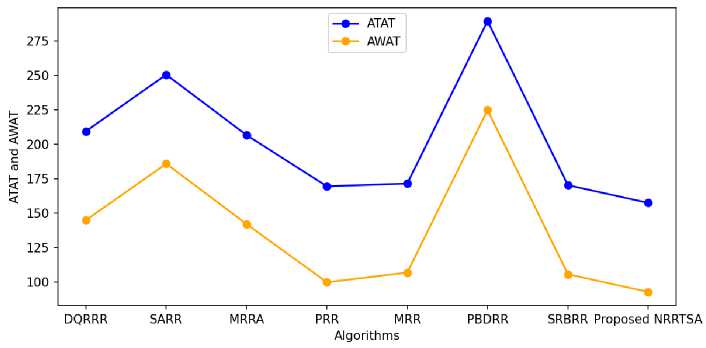
Fig.5. Comparison among Proposed NRRTSA and other RRTSAs for Dataset 1.

The Fig 7 has demonstrated comparison regarding average turn around time and average waiting time mentioned as ATAT and AWAT at Y-axis and legends. The values for this comparison have been received and observed from the table 2 for the dataset 3. Regarding ATAT, the last mentioned scattered point is for the proposed NRRTSA which smartly represents that the proposed method yields comparatively less average turn around time for the dataset 3. In addition to, concerning the AWAT, the last mentioned scattered point is also for the proposed NRRTSA which explicitly represents that the proposed method suffers comparatively less average waiting time for the dataset 3.

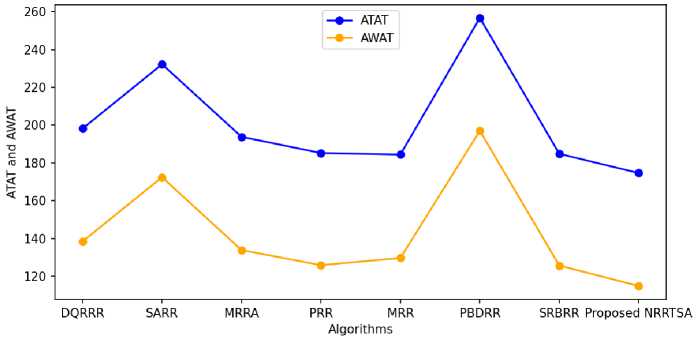
Fig.6. Comparison among Proposed NRRTSA and other RRTSAs for Dataset 2.

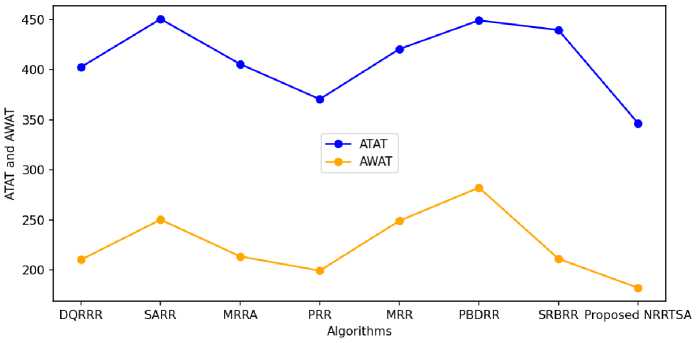
Fig.7. Comparison among Proposed NRRTSA and other RRTSAs for Dataset 3.

The Fig 8 has demonstrated comparison regarding average turn around time and average waiting time mentioned as ATAT and AWAT at Y-axis and legends. The values for this comparison have been received and observed from the table 2 for the dataset 4. Regarding ATAT, the last mentioned scattered point is for the proposed NRRTSA which smartly represents that the proposed method yields comparatively less average turn around time for the dataset 4. In addition to, concerning the AWAT, the last mentioned scattered point is also for the proposed NRRTSA which explicitly represents that the proposed method suffers comparatively less average waiting time for the dataset 4.

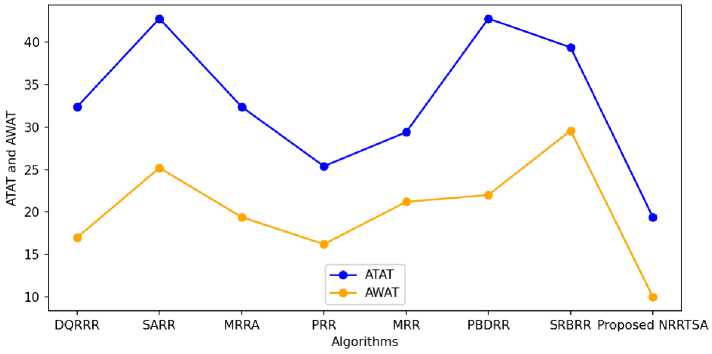
Fig.8. Comparison among Proposed NRRTSA and other RRTSAs for Dataset 4.

Fig. 9 has demonstrated the comparison of the proposed NRRTSA with other round robin task scheduling algorithms in terms of number of contexts switching. In the figure the X-axis labels all the round robin task scheduling algorithms, and Y-axis labels the number of contexts switching. The NCS of all the four datasets mentioned in the Table 2 have been represented. All the NCS have been represented as circle shape with pink filled color with green border color. In the Fig. 9, the 4 NCS values for 4 datasets of all the algorithms are not available due to overlapping. As for example, the proposed NRRTSA has one circle in the Fig. 9. It means the proposed NRRTSA yields the NCS = 6 for all the datasets available in the Table 2. Similarly, one or more indication of NCS is missing due to overlapping of the values.

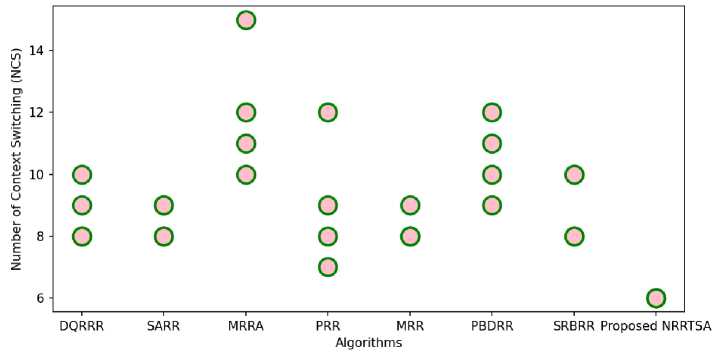
Fig.9. Comparison among Proposed NRRTSA and other RRTSAs on Number of Context Switching.

Having considered the result evaluation and discussion criterion, it can be stated that the proposed NRRTSA is comparatively effective and efficient. From Fig.5, Fig.6, Fig.7, Fig.8, and Fig.9 it has been demonstrated that the proposed NRRTSA is suitable for all types of datasets along with all different types of combinations. In all the figures, the orange line is for average waiting time, and the blue line is for average turn-around time. In Fig.9 the pink shaded green circles are for indicating NCS. The proposed NRRTSA is pictorially represented at most right corner of each figure. The novelty of the proposed NRRTSA is reducing the average turn-around time, minimizing average waiting time, and lessening the number of contexts switching massively in all types of datasets and all types combinations into the datasets. The cloud computing environment basically holds multitasking and multi combination based tasks with different types of arrival times. The proposed NRRTSA has acted like a generic and novel solution for all types of datasets, and all combinations of datasets into the cloud computing environment. The performance evaluation process of the proposed NRRTSA, and comparison of the proposed NRRTSA with other existing round robin task scheduling approaches have increased its acceptance and novelty.

6.    Conclusion

Cloud computing has become more beneficial IT service because of its incredible flexibility, and legitimate allocation of services or resources. The performance of the cloud computing environment inextricably depends on task scheduling. An efficient task scheduling ensures the legitimate allocation of resources corresponding to the requests generated by the tasks. This research has proposed a new round-robin task scheduling approach that enhances the performance of the allocation of resources from the central remote server in a cloud computing environment. As well as, the implemented NRRTSA has also determined an efficient time quantum for each round during scheduling. The experimental results and comparisons show that the proposed NRRTSA is comparatively efficient, and optimal than other existing round-robin task scheduling approaches for the cloud computing environment.

Our future work is to eliminate all the limitations involved in the proposed NRRTSA. The upcoming research will be an effort to constitute a sophisticated hybrid task scheduling approach with the combination of the round-robin strategy and starvation free prioritization method for all tasks. The combination between those two techniques can hopefully enhance and improve the performance of the task scheduling action with a higher accuracy and appropriateness in terms of resources allocation corresponding to the requests generated by all tasks in a cloud computing environment.