Optimized time efficient data cluster validity measures

Published Online April 2018 in MECS

The various characteristics of data such as size, high dimensions and noise definitely affect the performance of the clustering algorithms. Additional characteristics of this type of data are attributes and their scales. Various studies have been carried out to understand the manner in which the data distribution affects the performance of the different clustering algorithms. The main task of any clustering algorithm is to produce compact and well-separated clusters. Well separated and compact type of clusters cannot be achieved in practice. Different types of clustering validation are used to evaluate the quality of the clusters generated by clustering. These measures are elements in the success of clustering. Different clustering requires different types of validity measures. For example, unsupervised algorithms require different evaluation measures than supervised algorithms.

The clustering validity measures are categorized into two categories. These categories include external and internal validation. The main difference between external and internal measures is that external validity uses the external information and internal validity measures use internal information of the datasets. A well-known example of the external validation measure is Entropy. Entropy is used to measure the purity of the clusters using the given class labels. Internal measures validate the quality of the clustering without using any external information. External measures require the accurate value of the number of clusters in advance. Therefore, these measures are used mainly for selecting optimal clustering algorithms which work on a specific type of dataset. Internal validation measures are not only used to select the best clustering algorithm but also used to select the optimal value of the number of clusters. It is difficult for external validity measures to have predefined class labels because these labels are not available often in many of the applications. For these reasons, internal validation measures are the only solution where no external information is available in the applications.

All these clustering validity measures used currently are time-consuming and especially take additional time for calculations. There are no clustering validity measures which can be used while the clustering process is going on. The main contribution of this paper is designing optimized and time efficient cluster validity measures so that it can be used while the clustering process is going on.

The organization of this paper is as follows: Section I covers introduction, Section II presents a brief survey of the various literature related clustering and validity measures. The third section covers standard proposed time efficient cluster validity measures. In the fourth section, implementation and the results of this validity measures are discussed. In the last section, the conclusion and references are given.

• II.    Related Work

• A.    Clustering Algorithm

Clustering is a popular task wherein large heterogeneous datasets are segmented into an optimal number of homogeneous clusters.

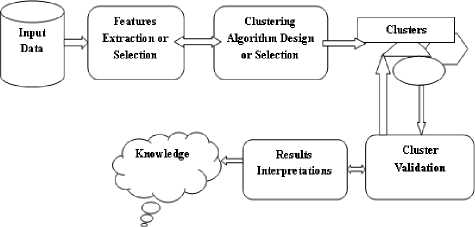
Fig.1. Clustering Process

The data clustering in the Figure 1 consists of various steps which are as given follows:

Feature selection or extraction: The feature selection step selects different features from a set of features and feature extraction generates the useful features selected using some transformation methods.

Clustering algorithm design or selection : This step helps to select existing clustering or design efficient clustering with clustering validity measures.

Cluster validation : This validation measure evaluates the quality of the clusters generated by the selected or designed clustering.

Results interpretation : Without user-friendly interpretation of the generated clustering results clustering is not useful. So, this step provides meaningful insights of the original dataset contents.

• B.    Standard Clustering Algorithms

k-means data clustering: k-means uses the partitioned based approach where the centroid is associated with each cluster and the data objects are assigned based on close centroids. But one of the issues with this method is to determine the value of the number of clusters and initial centroids. The detailed outline of this clustering is highlighted as follows:

Input: Data objects and k

Output: k clusters

• 1.    s elect k objects as initial centroids

• 2.   Repeat till no change in clusters

• 3.   Find distance between data objects and centroids

• 4.   Form clusters by assigning data objects to closest centroids

• 5.   Update centroids

Input: Data objects and k

Output: k clusters

Hierarchical clustering: This method generates nested clusters as results and is used to represent a special type of data structures. These clusters are organized in a hierarchical manner. The required number of clusters in this method of clustering is obtained by the cut algorithm. Following are the two types as discussed.

• 1.    Agglomerative:

Initially, this algorithm considers the datasets as a single cluster and merges it with closer clusters till only one cluster remains. The detailed steps of this are as given in the algorithm:

Input: Data objects

Output: k clusters

• 1.   Find proximity matrix

• 2.    Consider all data objects in one cluster

• 3.   Repeat till to form one cluster

• 4.   Merge two closest clusters

• 5.   Update proximity matrix

• 6.   Stop when criteria met

• 2.    Divisive:

The working of this clustering is exactly the opposite of agglomerative. Here, the clustering begins with one and an all-inclusive cluster and divides it into multiple clusters containing similar data objects. The outlines of this clustering algorithm are as given in the algorithm:

Input: Data objects

Output: k clusters

• 1.   Find proximity matrix

• 2.    Consider all data objects in one cluster

• 3.   Repeat still to form one cluster

• 4.   Merge two closest clusters

• 5.   Update proximity matrix

• 6.   Stop when criteria met

DBSCAN: One of the scalable density-based clusterings is the DBSCAN clustering. This clustering requires two parameters as user inputs. The first parameter is the number of data objects within a given radius (Eps) and the second is the core data objects (MinPts) within the radius. There are some special data objects called border objects that have fewer than MinPts within Eps. The detailed steps of clustering are as given in the algorithm:

Input: Data objects, MinPts, and Eps

Output: k clusters

• 1.    Arbitrarily selects p points

• 2.    Take all density reachable points using MinPts and Eps

• 3.    If point p is core point then form the cluster

• 4.    If point p is border point, then no point is density-reachable from p and visit next point

• 5.    Continue until all points are visited

Cluster validation process is an important step which can affect the success of all the clustering methods used in different applications. The main application of the cluster validity measure is evaluating the quality of the clusters generated by the clustering algorithms on the datasets. From the simulation and surveys, no clustering algorithm performs best for all of the validity evaluation measures. Most of the available validity measures cover only a subset of important aspects of the clusters. It is also found that these measures are complex and are not time efficient.

• C. Statandard Validity Measures

Performance evaluations of the clustering algorithms are not easy for counting the number of logical and syntax errors of the supervised learning algorithms. Generally, cluster validity measures available take the absolute values of the labels of the clusters into consideration. Measurement of the validity of the clusters nowadays is as important as the clustering algorithm itself. It is very difficult to select a clustering algorithm that performs well for all input datasets. One of the challenges in clustering is the varying and emerging high dimension data. Streaming type of input data may contain many features which affect the performance of clustering. This type of data surely hampers the performance of clustering and their evaluation measures. Following are the some of the validity measures [2][3][4] and its advantages and disadvantages:

Compactness. Cluster compactness is also known as the diameter and is a special measure used to validate clusters by using only the internal information of the dataset. Hence, the results of good clustering should cluster with high compactness. It measures the average distance between every pair of the data object in the same cluster.

Separation. Separation measures the degree of separation between individual clusters. Hence, the results of good clustering should be well-separated clusters. It measures the average distance between centroids and data objects into different clusters.

Dunn Index. This index measures the degree of compactness and the degree of separation between individual clusters. It measures the inter-cluster distance over intracluster distance.

Homogeneity: It is defined as the validity measure which ensures the quality of the clusters by checking the assignment of the data objects for a single class in only one of the clusters formed.

Completeness: It ensures that the elements in a single cluster should be of the same class.

Advantages of these measures are as follows:

• 1    Its score is bounded from 0 to 1.

• 2    It gives an intuitive interpretation of the score.

• 3    Its working does not depend on the structures of the cluster.

The drawback of these measures is as follows:

• 1    These validity measures are not normalized with respect to random labeling of data.

Silhouette Score. The Silhouette is a well-known measure of cluster validity. It measures the average distance between data objects and all other data objects in the same class. Also, it measures the average distance between data objects and all other points in the next closest cluster. Advantages of this measure are as follows:

• 1    This measure has the bounded score between -1 for bad clusters and 1 for good quality clusters.

• 2    The score of this measure is high for clusters which are dense and well separated.

Disadvantages are as follows:

• 1.    The score of this measure is high for the convex type of clusters.

Calinski-Harabaz Score. It is the average mean between-cluster dispersion and the within-cluster dispersion. Advantages of this measure are as follows:

• 1.    The value of this measure is higher for dense and well-separated type of clusters

• 2.    Compared to the other scores this score is fast to compute.

And the disadvantage of this measure:

• 1.    This score is higher for these types of clusters.

The clustering process is considered as the well known unsupervised learning method because it divides the data objects into clusters by ensuring that the data objects in one cluster are similar in nature and data objects in two different clusters differ from each other. Application areas of clustering range from science to technologies. Some of the applications include analysis of various images and bioinformatics. Because clustering is an unsupervised task, it is needed to find a technique to validate the quality of the clusters generated by this clustering. Otherwise, it may create issues in the analysis of the different results of clustering.

As discussed in the earlier section, clustering validation is used to evaluate the performance of the clusters and there are two types, internal and external. Therefore, authors Junjie W et al. in focus on the various types of internal cluster validity measures [5][6]. They have studied and simulated these measures on different datasets and present a brief summary of their study on eleven widely used internal crisp clustering validation measures.

The clustering process is also known as cluster analysis and is becoming an important commonly performed step to analyze gene expression profile data. Nowadays one of the challenges of clustering algorithms is the selection of the clustering algorithm from an impressive list of clustering available. Hence, the authors Susmita D et al. propose two novel cluster validation methods [7]. This method has two parts. The first part measures the statistical consistency of the clusters formed and the second measures the biological functional consistency. For a good clustering algorithm, these values should be small.

For the past few years, the quality of clusters generated by different clustering algorithms [15]-[18] is one of the vital issues in the clustering application areas. It is found that most available clustering validity measures are geometry based because the score of these measures is high for this particular type of clusters. Therefore, authors Duoqian M et al. use the model decision theory and various loss functions to propose innovative cluster validity measures. Hence, this measure helps to find the value of the number of clusters [4]. The proposed clustering validity has the ability to deal with monetary values and hence, it differs from the other distance-based validity measures. It is possible to extend the proposed clustering quality measure for performance evaluation with different clustering algorithms such as the fuzzy type of clustering algorithm. From the experiments and simulation of these cluster validity measures for various clustering algorithms on different types of datasets, it is found that these measures are more time consuming and there is no cluster validity measure that is available which can be used while the clustering process is going on.

Various clustering algorithms are discussed in the above sections. In these methods, the clustering relies on a random component. Along with consistency, the stability of the cluster is also an important criterion to compare different clustering methods. Stability is considered as an asset of the clustering process. One of the techniques to overcome the instability problem is the use of cluster ensembles [8]. In this paper, authors use the k-means based clustering ensembles technique. Through this method, each cluster is assigned a number of clusters randomly using initialization. Then the clustering is adjusted and an index is used to define pairwise stability, and entropy is used to define non-pair wise stability.

The basic purpose of clustering is to produce as many clusters as possible. But there should be a proper mechanism to assess the quality clusters generated by clustering. Hence, there is a requirement for cluster validity measures. The authors propose a new cluster validity measure which helps find the optimal value number of clusters produced by the fuzzy clustering and its subtypes [9]. This measure is used to measure the cluster overlap and separation of each data object. This measure uses aggregation operation of the membership degrees.

There are two important elements in cluster analysis. These elements are the clustering algorithm and cluster validity. Qinpei Z et al. propose innovative ideas for both algorithms and cluster validity measures [10]. Here, the centroids ratio is defined to compare results of a newly proposed prototype-based algorithm which is based on the pairwise random swap techniques. This ratio is highly related to the sum square error and other types of validity measures. From the experiments, it is also found that this ratio is simple and fast for calculation.

The authors of this paper propose an innovative method of cluster validity [11]. This new validity measure is not dependent on fuzzy membership, rather it depends on the neighborhood information of data objects to analyze cluster structure. Also, this measure is different from the other because it is not sensitive to find the distance between data objects and its centroids. In this paper, the authors also propose a new clustering method. This clustering prevents this validity measure from the errors which are introduced by the fuzzy membership matrix. The advantage of this newly proposed measure is that it can be used for both hard and fuzzy clustering algorithms. This property measure makes it more useful and a more widely used validity measure without requiring any information about the shape of the clusters. This measure has some issues also. As the measure is the average of the radius of a cluster there is a likelihood that it may go wrong for the thin and longline shape of clusters.

Many authors discuss that clusters generated by the k-means clustering should be more compact and well separated. But some of the types of k-means clustering are dependent on the intracluster compactness rather than inter cluster separation [12]. So to end this, authors Haijun Z et al. propose an innovative clustering method using the principles of k-means clustering with a focus on compactness and separation. The authors designed objective functions and using these functions new clustering updating rules are derived for the clustering.

In recent research, a more popular way to enhance the performance of clustering is to make a consensus of clustering. The main objective of this clustering is to find single partitioning results by combining the different results of similar or different methods. This method is popular because it finds quality clusters from the heterogeneous datasets. In this literature consensus clustering using k-means is proposed by the authors Jie C et al. with their necessary and sufficient conditions [13]. This condition can help develop a framework for this type of clustering on the complete as well as incomplete datasets. The authors comment that there are some factors which may affect the quality and diversity of standard clustering and consensus clustering. To upgrade the working of clustering, dimension reduction methods may be useful.

Clustering algorithms are used in many different fields [20]-[21]. The authors in the paper [14] present a brief study of dimensional reduction techniques in the k-means clustering. This technique consists of two approaches: the first is feature selection and second is feature extraction. The first feature selection in clustering selects the subsets of the input features and performs clustering on the selected features. The second constructs the artificial features from the selected features and then performs clustering on these constructed features.

• III.    Proposed Cluster Validity Measure

From the above-related work on existing and enhanced cluster validity measures, it is observed that no work is available in designing time efficient cluster validity measures. All measures discussed above are complex and are used after the clustering process is complete. But from the surveys and simulation, it was found that these measures are not very time efficient. For large data, these measures take more time to just compare the algorithms. This research has surveyed the existing and improved cluster validity measures. It then proposes time efficient and optimized cluster validity measures. These measures use the concept of cluster representatives and random sampling. The work proposes optimized measures for cluster compactness, separation and cluster validity. These three measures are simple and more time efficient than the existing clusters validity measures and are used to monitor the working of the clustering algorithms on large data while the clustering process is going on. Instead of considering all the data objects in the given datasets, these measures find the cluster representatives using the random sampling method. Then it calculates compactness and separation of these random samples. So, this random sampling method minimizes the required time. The outlines of these measures are presented in the following sections.

• A.    Algorithm to Find Cluster Representatives

• 2.Find clusters representatives cluster_representatives=random(clusterpoints, num_samples)

This algorithm finds the number of cluster representatives from original clusters using random sampling.

Input: Clusters, k

Output: Compactness and separation value Step 1: Find Cluster Representatives 1. Find number of clusters representatives no_points = points in cluster if no_points == 1 cluster_representatives=centoid if no_points <= k num_samples = k/2 if no_points > k num_samples = k/2 if no_points > (2*k) num_samples = k

The flow of this algorithm is depicted in Fig 1:

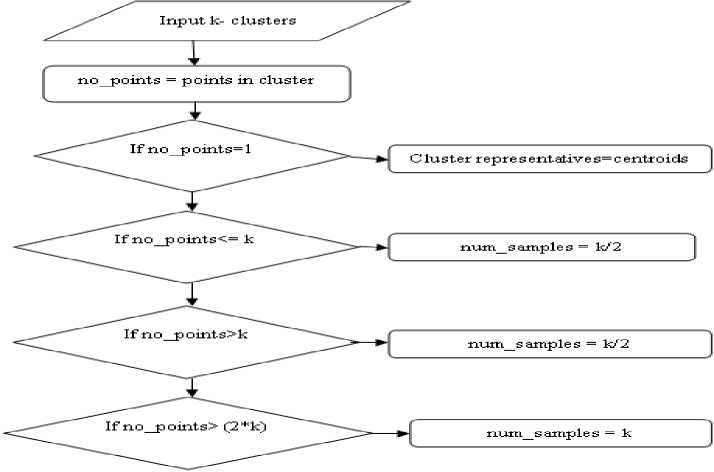
Fig.2. Flowchart to Find Cluster Representatives

• B.    Algorithm to Find Optimized Compactness

This algorithm finds the optimized compactness using cluster representatives selected in the following algorithm.

• D. Optimized Validity Measure

This algorithm finds the value of optimized cluster validity measure using optimized compactness and separation calculated in the following algorithm.

Step 2: Find Optimized Compactness

• 1.    Take all the formed clusters and their centroids, Ci.

• 2.    Select k random samples, Ri from each centroid using random sampling method.

• 3.    Find compactness of individual cluster, k using random samples and centroids

• 4.    Final Compactness

• 5.    The low value of Compactness indicates more compact clusters.

Ri = {r1, r2, rk}

Local compactness (ki) = max (d (Ri, Rj), where i and j are the elements in a cluster.

Compactness= ( ∑ Local compactness (ki))/Number of

Clusters

The flow of this algorithm is depicted in Fig 2:

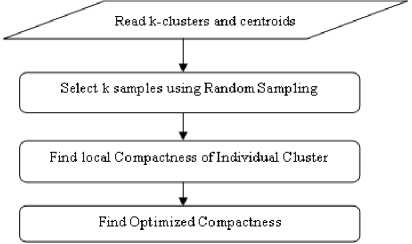
Fig.3. Flowchart to Find Optimized Compactness

• C. Algorithm to Find Optimized Separation

This algorithm finds the value of optimized separations using cluster representatives selected in following algorithm.

Step 3: Find Optimized Separation:

• 1.    Take all the formed clusters

• 2.    Calculate distances = (∑| (ri-rj) |) / number of random samples in Rj. Where i and j are elements in i and j clusters.

• 3.    Find the local separation

• 4.    Final separation

• 5.    A higher value of Separation indicates well-separated clusters.

Local separation (Ri, Rj)= min(Distances)

Separation=(∑Local separation (Ki))/(Number of Clusters*Number of Clusters)

The flow of this algorithm is depicted in Fig 3.

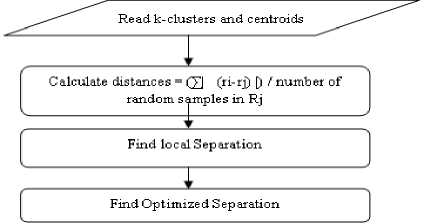
Fig.4. Flowchart to Find Optimized Separation

Step 4: Find Optimized Validity Index:

• 1.    Take value of optimized compactness and separation and Calculate the value of optimized validity measures

Optimized validity Index=Optimized separation/ Optimized compactness

• E. Advantages of Proposed Measures

Following are the advantages of this proposed optimized cluster validity measure.

• 1.    This measure is less complex.

• 2.    This measure uses more than one cluster representative for calculating compactness and separation. Hence this measure offers more accurate result.

• 3.    An optimized measure is used to monitor the working of the clustering algorithm on large data for more accuracy while the clustering process is going on.

• IV.    Results Analysis

  This measure is implemented using Python programming language. After implementation, the proposed algorithm is applied to various datasets. The performance of the proposed measures is compared with existing measures using runtime required to calculate the values of this measure. To compare the advantages of the proposed time efficient clustering validity measure over the standard measures this research work uses various real datasets from the Kaggle site. These datasets include accident data, airline clusters, automobiles, cities, cancer data, computer, happy and health datasets. The minimum number of records and variables are 157 and 7 respectively. The maximum number of records and variables are 6259 and 15 respectively. Following Table 1 shows the details of datasets used to simulate the results of proposed measures.

Table 1. Datasets Used

SN	Datasets	Number of instances	Number of attributes
1	Accident	2057	15
2	Airline clusters	3999	7
3	Automobile	195	14
4	Cities	493	10
5	Cancer	228	10
6	Computer	6259	8
7	Happy	157	10
8	Health	202	13

Datasets used for the algorithm are benchmark datasets because these datasets are used by various researchers in the above literature.

This proposed clustering evaluation measure is implemented in the Python programming language on the Linux operating system. The validity of this measure is evaluated by the quality of the cluster while the clustering process is going on. This measure is more time efficient than the existing clusters quality evaluation measures. The performance of this measure is compared with existing compactness and separation measures using run time required to calculate the value of this measure. The sample output of this measure is given in the following the figure:

(- 9 Accuracy: 95.91

Clustering matrix efficient:

122132121311233333333211 1133113444645464665656456565555444456666 5 9 ? 8 9 91 8 9 8 9 9 9 7 7 9 9 8 8 7 9 7 ■ 7 9 В 7 7 9 8 8 8 9 7 [1, 2, 2, 3, 3, 2, 1, 2, 1, 3, 1, 1, 2, 3, 3, 3, 3, 3, 3, 3, 3, 2, 1, 1, 1, 1, 3, 3, : 1, 3, 4, 4, 4, 6, 4, 5, 4, 6, 4, 6, 5, 5, 6, 5, 6, 4, 5, 6, 5, 6, 5, 5, 5, 5, 4, 4, 4, 4, 5, 6, 6, 6, 6, 5, 9, 7, 8, 9, 9, 8, 1, 8, 9, 8, 9, 9, 7, 7, 9, 9, 8, 8, 7, 9, 7, В, 1, 9, 8, 7, ?, 9, 8, 8, 8, 9, 7]

total points: 99 Outliers: 8

Predicted K: 9

iccuracy: 95.91

Compactness : 1.62

Saperation : 8,18

Dunn Index: 9.1116

rifle Required for conpactness and separation: 0.8617166929999499698

Calinski-Harabaz Index : 264.63

DB index: 1.13

Optimized Conpactness: 2.93

Optimized Separation: 2.98

Optimized Validity Index: 1.4634

rifle Required for Optimized conpactness and separation : 8.69835825188667969813

[python3envj anand8anand-LeHro-G5a-8B:-/python$ |

Fig.5. Output of Proposed Validity Measure

Table 2. Comparative Results of Measures

SN	Datasets	Enhanced Scalable k-means
1	Accident	Existing Measures	Proposed Measures
		Compactness : 7950.13	Optimized Compactness: 3813.07
		Separation : 21.89	Optimized Separation: 1905.68
		Dunn Index: 0.0028	Optimized Validity Index: 0.4998
		Time required for existing measures: 0.000776	Time required for proposed measures: 0.0000263
2	Airlines clusters	Compactness : 593070.11	Optimized Compactness: 37127.45
		Separation : 222.1	Optimized Separation: 71972.77
		Dunn Index: 0.0004	Optimized Validity Index: 1.9385
		Time required for existing measures: 0.00285	Time required for proposed measures: 0.000312
3	Cities	Compactness : 1424232.56	Optimized Compactness: 228411.65
		Separation : 611.9	Optimized Separation: 638389.33
		Dunn Index: 0.0004	Optimized Validity Index: 2.7949
		Time required for existing measures: 0.00354	Time required for proposed measures: 0.000740
4	Automobile	Compactness : 14672.13	Optimized Compactness: 2980.41
		Separation : 180.51	Optimized Separation: 3828.76
		Dunn Index: 0.0123	Optimized Validity Index: 1.2846
		Time required for existing measures: 0.00227	Time required for proposed measures: 0.000740
5	Cancer	Compactness : 649.57	Optimized Compactness: 333.4
		Separation : 30.45	Optimized Separation: 456.8
		Dunn Index: 0.0469	Optimized Validity Index: 1.3701
		Time required for existing measures: 0.002439	Time required for proposed measures: 0.0000536
6	Computer	Compactness : 2837.01	Optimized Compactness: 1909.64
		Separation : 14.66	Optimized Separation: 1320.94
		Dunn Index: 0.0052	Optimized Validity Index: 0.6917
		Time required for existing measures: 0.000514	Time required for proposed measures: 0.00000791
7	Happy	Compactness : 2.25	Optimized Compactness: 3.07
		Separation : 0.22	Optimized Separation: 2.43
		Dunn Index: 0.0995	Optimized Validity Index: 0.7909
		Time required for existing measures: 0.003472	Time Required for proposed measures: 0.000888
8	Health	Compactness : 153.69	Optimized Compactness: 169.41
		Separation : 10.43	Optimized Separation: 82.22
		Dunn Index: 0.0679	Optimized Validity Index: 0.4853
		Time required for existing: 0.00230	Time Required for proposed measures: 0.000679

This measure is used to evaluate the quality of the enhanced scalable clustering algorithm and k-means clustering algorithm. And it is found that the proposed measure is more time efficient than the existing measures. The results of this measure are shown in Table 2.

The average runtime of the proposed cluster validity measures is reduced by at least 25% than the existing cluster validity measures. The performance analysis of these measures is also shown in the following the Figure 5 and Figure 6.

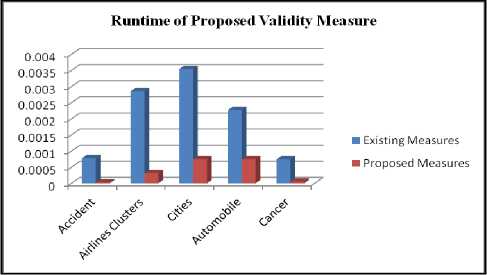
Fig.6. Runtime of Proposed Validity Measure

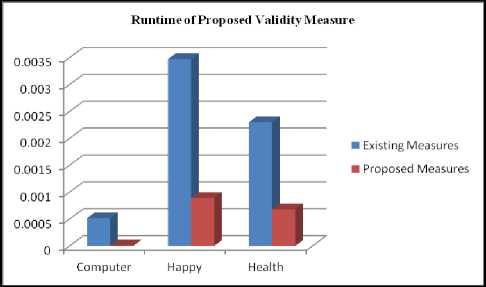
Fig.7. Runtime of Proposed vs. Existing Measure

Various existing measure are also implemented for the above datasets. Then runtime for standard separation and compactness and Dunn index is calculated. From the figure 6 and figure 7, it is observed that average runtime of proposed measure is reduced for all the data sets. For some datasets, standard measures are taking to much time to calculate index value. But the proposed measures are to faster than these standard measures. For all the datasets, proposed measure is taking at least 25% time to calculate index value.

• V.    Conclusion and Future Work

This paper surveyed and studies the various existing and improved cluster quality measures. From the simulations of these measures, it is found that these measures are time-consuming. Also, all these measures are used to complete the clustering process. No measures are developed to check the performance of the clusters while the clustering process is going on. Hence, this work proposes time efficient cluster validity measures while clustering. These measures use the concept of cluster representatives and the random sampling method. This work proposes optimized measures for cluster compactness, separation and cluster validity. The measures are simple and more time efficient than the existing clusters validity measures. These three measures are used to monitor the working of the clustering algorithms on large data while the clustering process is going on. From the experiments of this measure on various datasets, it is observed that the average runtime of this measure increases by 25 % than the existing cluster validity measures.