Optimizing parameters of automatic speech segmentation into syllable units

Published Online May 2019 in MECS DOI: 10.5815/ijisa.2019.05.02

A speech segmentation is one of important subsystems in the automatic speech recognition (ASR) since a speech should be segmented into basic units, such as words, syllables, morphemes or phonemes before recognizing it [1]. In syllable-based ASR system, it is generally used in conjunction with a syllabification model, such as described in [2].

There are two approaches of speech segmentation, i.e. time-domain approach [3,4] and frequency-domain approach [5-7]. The time-domain approach, which is commonly based on a Short-Term Energy (STE), requires a low computation but less accuracy than the frequencydomain one. In contrast, the frequency-domain approach, such as a minimum phase group delay function described in [8], gives a better accuracy but more computations.

However, the STE-based approach is good enough for defining syllable boundaries since a high energy in STE generally corresponds to a vowel utterance that is a nucleus of syllable. Hence, many researchers develop a syllable segmentation based on an STE [3,4].

The problem of an STE-based syllable segmentation is that it needs a fixed threshold that should be determined using a manual observation as described in [3,4]. In this paper, an adaptive threshold method that is automatically inducted by learning a set of utterances is proposed to detect a syllable boundary

The works related to the syllable speech segmentation will be discussed in Section 2. The proposed syllable segmentation method is explained in Section 3. The proposed GA-based optimization of parameters is described in Section 4. Next, the results of experiments and observations as well as the discussion are given in Section 5. Finally, some conclusions are provided in Section 6.

• II.    Related Work

In general, there are three metrics used to evaluate a speech segmentation, i.e. accuracy, insertion error, and deletion error [3]. The accuracy is the ratio between number of correct segment and the total segment in the sentence. The insertion error is defined as the number of unexpected boundaries while the deletion error is defined as the number of the deleted expected boundaries.

In [3], an Indonesian syllable segmentation is developed using an STE smoothed by a fuzzy-based model. A local normalization and a fixed threshold are well designed to improve the system. Besides, two postprocessing procedures (splitting and assimilation) are applied to increase the accuracy and reduce the errors. The splitting procedure splits a segment into two shorter sub-segments while the assimilation procedure groups two segments into a longer segment [9]. But, both splitting and assimilation are performed once only, not iterative, so that the splitting cannot split a segment into more than two segments and the assimilation cannot combine more than two segments into a bigger one [9].

A splitting procedure functions to reduce deletion and increase accuracy while the assimilation functions to reduce insertion [3]. Some experiments using Automatic syllable segmentation with Local Normalization and Splitting (ALNS) gives 0.8% better accuracy and 0.77% less deletion but with 1.06% greater insertion error than the Automatic syllable segmentation with Local Normalization and sequentially combined Splitting and Assimilation (ALNSA). But, ALNSA fails to increase accuracy and reduce deletion error. It shows that the assimilation procedure over-merges the expected segments and keeps the unexpected insertion. In [3], the researchers states that the sequentially combined splitting and assimilation procedure does not work properly.

Both splitting and assimilation are the threshold-based methods to determine whether a segment should be split into two segments or be grouped into its neighbors [9]. Similar to the boundary detection threshold, an adaptive threshold could also be applied in the splitting and assimilation parameters by learning from the speech data [9]. Hence, the parameters of boundary detection, splitting and assimilation can be tuned to become the adaptive thresholds.

There are many methods to generate adaptive thresholds, such as Bayesian Network (BN) [10], Deep Neural Network (DNN) [11], Simulated Annealing (SA) [9], Dynamic Window (DW) [12], and Hidden Markov Model (HMM) [13]. Since the parameter tuning can be seen as an optimization problem, an evolutionary computation such as GA can be applied.

Unlike BN [14], DNN [15] or HMM [16] that relies on an optimal structure to produce the best result, GA uses a chromosome to represent a solution. The chromosome length corresponds to the number of parameters to be optimized. Unlike SA that relies only on a single agent, GA has many searching agents so that it can find the global optimum faster than SA [9]. Another benefit is GA can be used as a multi-objective optimization to minimize both insertion and deletion errors [17-18].

The boundary detection, splitting, and assimilation procedures are sensitive to parameter tuning since they are threshold-based methods [9]. The thresholds of those methods can be fixed, not adaptive from the speech data, which are obtained by manual observation as used in [3]. This method may give worse result when the assimilation procedure over-merges the expected segments and keeps the unexpected insertion [3].

Hence, optimizing parameters of the boundary detection, splitting, and assimilation is proposed to improve the sequentially combined splitting and assimilation to increase accuracy, reduce deletion error and insertion error. Two improved splitting and assimilation called an iterative-splitting and an iterative-assimilation are also proposed. Both improved procedures iteratively repeat the splitting or assimilation until there is no change in the resulted syllable segments to increase the accuracy as well as reduce the insertion and deletion errors. Thus, in this paper, the previous splitting and assimilation used in [3] are referred to non-iterative-splitting and non-iterative-assimilation.

• III.    Proposed Syllable Segmentation

The block diagram of the proposed automatic speech segmentation into syllables is illustrated by Fig. 1. Two new post-processing methods called iterative-splitting and iterative-assimilation (in grey color), are proposed as the modification from the previous methods in [3].

Speech

Pre-processing

Short Term Energy

Normalization

Silence Removal

Boundary Detection

Iterative-Splitting

Iterative-Assimilation

Segments of syllables

Fig.1. Proposed syllable segmentation.

• A.    Pre-processing

This procedure starts with the subtraction of the signal samples using a formula yi =xi -αxi-1                   (1)

where x is the value of the i th sample and α is the preemphasis coefficient. The value of α used in this experiment is 0.9, which is the same value used in [3,19]. This procedure is used to spectrally flatten the speech signal causing the perseverance of high-frequency components of the samples.

The subtracted signals are then framed into 10 ms using hamming windows. The sampling frequency is 8 kHz so that each frame contains 80 samples. To get the smooth features, each frame contains 60 overlapping samples or 75% of the frame.

• B.    Short-Term Energy

Each frame is then converted into an STE that is calculated using a square energy since it empirically gives the best accuracy for Indonesian speech dataset as described in [3]. The calculation of the STE is performed using a formula

N

E    X S 2                  ( ² )

j = 1

where E is the STE of the i th frame, N is the total number of samples in the i th frame and S is the value of the j th sample in the i th frame.

• C.    Normalization

The normalization of STE is performed to adjust the amplitude differences in the Indonesian speech sentence. Some part of the speech may contain high amplitude but the other part may also contain really low amplitude while it was supposed to be a syllable segment as explained in [3]. In this research, the normalization is calculated using

M i =

( E i - min ( E ) )

( max ( E i ) ^- min ( E ) )

where M and E are the normalized and the original STEs in the i th frame of the sentence respectively.

• D.    Silence Removal

This procedure eliminates any STE that is less than a certain threshold to remove both silences and noises. The normalized STE is inspected if it falls below the value of threshold S 1 . If it is below the threshold, the energy is removed. The value of S 1 is 0.001.

• E.    Boundary Detection

  The proposed boundary detection method needs the optimum parameter to detect a boundary. An expected boundary of a syllable segment is detected by the combination of procedures described in [4,9]. There are four parameters needed in this method, i.e. radiusStep , dmax , dmin , and thmin . These parameters are optimized using GA and will be explained in the next section. The radiusStep is the number of frames as the range to evaluate a local minimum energy of a frame. For example, if a speech contains 1000 frame and the radiusStep is 4, then there will be 250 local minimum energies. It means each segment has four energies and each energy will be examined as a local minimum. If the number of frames is not divisible by the radiusStep , then the last segment has a different number of frames that is the modulo of the number of frames and the radiusStep . If the radiusStep is 3, then there will be 334 segments and each segment has 3 possible energies. Consequently, the number of possible energy of the last segment is 1. If there is only one energy in a segment, then the energy is still considered as the local minima.

First, all local maxima of the normalized STE within the radius of radiusStep are taken. A local maximum is defined as the maximum energy within the range of the radiusStep. Each local maximum is evaluated to check if there is another energy in its neighborhood that is greater than the evaluated local maxima energy. If there exists no energy to satisfy that evaluation, then the local maxima are changed into maxima. The neighborhood of the evaluation is defined in parameter dmax.

The parameter dmax is the number of the neighbor frame on the left and the right of a frame. If there is no neighbor on the left, then only the right neighbor is considered and vice versa. For example, if the value of dmax is 1, then for each local maximum, there will be one neighbor on the left and the right of the frame. The neighbor is the other local maxima, not just the frame next to the local maxima. The neighbors are evaluated to select the maxima. The selection criterion used here is “If there is another energy on the neighborhood of the local maxima, then it is selected as the maxima. If the local maximum has the highest energy in the neighborhood, then the it is selected as the maxima.

All maxima taken from the previous evaluation are needed to find a local minimum. A local minimum is a minimum energy that occurs between two maxima. In this method, each local minima needs to be inspected. If there is no other energy that is less than the local minimum in the neighborhood of dmin , then the local minimum is compared to energy threshold thmin . If it is less than thmin , the local minimum is the expected boundary.

The parameter dmin follows the same concept as the dmax , but the neighbor is the frame next to the evaluated local minima. This implies that dmin and dmax has a different context of the neighbor. The values of both dmin and dmax , equal or not, do not affect the algorithm since they function to evaluate the local minima is either a maximum or a minimum in its neighborhood. The higher dmax or dmin the more the number of frames to evaluate. In other words, The higher dmax or dmin the stricter the selection process.

• F.    Iterative-splitting

The iterative-splitting parameters need to be tuned properly to achieve the optimum performance. In [3], the parameters are tuned manually by observation. Instead of manual observation, the splitting parameters in this research are tuned using GA to get better tuning. Those parameters are splitStep, shortLengthSplit, shortRatioSplit and longRatioSplit. These parameters have the same concept as the radiusStep in the previous segment, which is the range of the frames.

This procedure starts by inspecting all of the expected syllable segments in the sentence. All local maxima between the radius of splitStep are taken. Between two local maxima, a local minimum is searched. Then, the local minimum is temporarily assigned as a boundary between the two divided segments. Next, the ratio between the closest local maximum to the local minimum and the local maximum is calculated. This ratio is referred to rMaxMin .

The rMaxMin is the local minimum energy divided by the closest local maximum energy, which is a temporary boundary. There are two possible positions of the local maxima to the temporary boundary, which are either on the left or on the right. Between the two possible local maxima, the closest one to the local minimum energy is selected. The selected local maximum refers to the closest local maximum energy.

The shortLenghSplit is a threshold to examine if the splitting is categorized as a long or a short splitting. The long splitting means that the segment contains many frames those are higher than the value of the shortLengthSplit . If the number of frames in the segment is less than the shortLengthSplit , then the splitting is categorized as a short splitting.

The shortRatioSplit and LongRatioSplit are the energy thresholds to examine if a local minimum is an expected boundary or not. If so, then the segment is split into two segments. The long splitting uses the longRatioSplit as the evaluation while a short splitting uses the shortRatioSplit . If the temporary boundary is greater than either the shortRatioSplit or the LongRatioSplit , then the segment is split and the temporary boundary becomes the expected boundary.

The shortest syllable segment from the two divided segment is searched and compared with the shortLengthSplit . If it is greater than shortLengthSplit then the rMaxMin is compared with the longRatioSplit . On the contrary, the rMaxMin is compared with the shortRatioSplit . If the rMaxMin is greater than the shortRatioSplit or rMaxMin is greater than longRatioSplit , the temporary boundary is not removed. Hence, it becomes the new boundary resulted from the iterative-splitting. The procedure is repeated until there is no splitting occurred, which implies that it is repeated until there is no additional boundary.

• G.    Iterative-assimilation

Like the iterative-splitting, the iterative-assimilation is repeated until there is no change in the syllable boundary. The parameters of iterative-assimilation also need to be tuned. Three parameters of assimilation used in [3], i.e. maxFricativeRatio,     averageFricativeRatio,     and decreasingResidualRatio are observed manually.

To calculate STE or residual energy, the signal is cut off using a low pass filter of 2800 Hz. The calculation of the energy is computed similarly like the total energy, which is computed using the square energy explained in the previous subsection.

The iterative-assimilation method works similarly like the assimilation method in [9]. First, all segments in the sentence are inspected. Then, each segment is checked if it is categorized as a fricative. Next, the fricative is given two possible directions to assimilate, which is to the left segment or the right segment of the fricative.

The parameter maxFricativeRatio is a threshold that is compared to the ratio of the maximum residual energy and the total energy in the same frame as the maximum residual energy. If the ratio is greater than the maxFricativeRatio , then the segment passes a criterion of a fricative.

The averageFricativeRatio is a threshold that is compared to the average of the residual energy of all the frames in a segment. If the ratio is greater than the averageFricativeRatio, then the segment passes the second criteria to be considered as a fricative.

A segment is categorized as a fricative if it meets two conditions: 1) the ratio between the maximum energy occurred in the residual energy and the total energy in that position is greater than maxFricativeRatio ; and 2) the ratio between the average residual energy of the fricative segment and the total energy in that position is greater than averageFricativeRatio .

The decreasingResidualRatio is a threshold that is compared to the ratio between the maximum residual energy in a segment and the residual energy of the last frame in the segment. It functions to examine whether the trend of the fricative is decreasing or increasing.

To determine whether the fricative is assimilated to the left or to the right segment, the trend of the fricative needs to be evaluated. If the trend is decreasing, then the fricative is assimilated to the left of the segment. On the other hand, if it is increasing, the fricative is assimilated to the right of the segment. The trend of the fricative is decreasing if it is met with 2 criteria. First, the location of the maximum residual energy of the fricative is in the first frame of the segment. Second, the ratio between the maximum residual energy and the last energy in the segment is greater than decreasingResidualRatio .

• IV.    GA-based Parameter Optimization

In the previous section, there are several parameters should be tuned properly using an optimization method. The optimization method used in this research is GA. There are three groups of parameters categorized by its method, i.e. boundary detection parameters, iterative-splitting parameters, and iterative-assimilation parameters. The GA is performed separately based on the group.

The type of encoding used in this GA is the binary encoding. There are two types of variable in the parameters, which are the integer types and real types. Thus, the parameters are grouped into two sets according to its type. The first set is the integer set and the latter is the real set.

For the integer set, the encoding procedure starts with the calculation of each range of the member denoted by r . This range is a subtraction of the maximum value of the parameter by the minimum one and an addition by 1. Then a formula

N

Lint = E log2 ri i=1

Z 2 =

E 2 + a

is applied to find the chromosome length of the integer type parameters that refers to L , where N is the cardinality of the integer set.

For the real set, the encoding procedure starts with determining the precision of the real number denoted by c . Then, similar to the range calculation of the integer set member, the range is also computed for each member of the set referred to b . The total length of the real type parameters L is then computed using

N

L real = E !OS 2 ( Ь^ c ) (5) i = 1

Finally, the chromosome length L for each individual is calculated using

^L = L int ^{+ L} real ⁽⁶⁾

The initialization of the population begins with randomly generating n individuals. The n _ind is the total individuals in the population. There are other configurations to be done which are the percentage of the crossover operation denoted by v , the percentage of the elitism individuals kept denoted as v and the percentage of the mutations denoted by v .

Next, a decoding procedure is performed to evaluate the individual fitness. The individual is divided into subindividual. Each sub-individual represents a parameter. Each sub-individual is taken from the corresponding start index until end index of the individual chromosome. Then each sub-individual is converted into a decimal, followed by the addition by 1. For the integer type variable, the decoding process is finished. Meanwhile, the real-valued parameters are furthermore computed using

>real = d ХЮ" c

to decode the sub-individual into parameters, where D is the decoded sub-individual, d is the converted value, and c is the chosen precision value as previously defined in the encoding procedure.

After decoding the parameters, each individual is evaluated based on a multi-objective fitness function. The weighted sum approach explained in [17] is used here as the basis of the fitness calculation. Z and Z are two objective functions formulated as where E is the insertion error, E is deletion error, and a is a small real number to prevent a division by zero. The value of a used in this optimization is 0.000001. The fitness f is then formulated as f H

;         a , ( Z 1 + Z 2 ) < 0

w 1 Z 1 + w₂ Z 2 , ( Z 1 + Z 2 ) > 0

where w and w are the weights of the corresponding objective functions and

2 _w

4—1 i = 1   i

= 1. An insertion error is defined as the percentage of additional syllable boundary that occurs within the radius of 50 milliseconds from the expected one. In contrast, a deletion error is the percentage of the missed boundary.

After evaluating the individual fitness, an elitism procedure is carried out. All individuals in the population is ranked based on their fitness. Then, the best individual is kept as a survivor for the next generation.

In this research, a parent selection is performed by a roulette wheel method as described in [20]. All individuals are sorted ascendingly based on its fitness then the cumulative fitness is computed. Thus, a real number is randomly generated in the interval [0, 1]. If the random number is in the certain individual cumulative fitness, then that individual is selected as a parent.

Next, a crossover is carried out using three selected parents since the type of crossover in this method is the three parent crossover [21]. Three parents p , p , and p are selected using the roulette wheel procedure. All genes in p and p are then compared. If they are equal, then the corresponding gene is inherited to the offspring in that position. Otherwise, the offspring receives a gene from p in the corresponding position. The crossover rate is denoted by n .

A mutation procedure is performed by inverting the binary genes. The mutation rate is denoted by n . The selection of the individual to mutate also use a roulette wheel procedure. Once an individual is selected, all genes in the individual are inspected. For each gene, generate a real number randomly in a range [0, 1] and then examine it. If the number is greater than 0.5, then the gene is inverted.

The GA procedure is terminated if it reaches either a stagnancy or a certain iteration limit. The stagnancy is defined as no improvement of the best individual for N generations while the iteration limit is defined as N .

and

Z 1 =

E + a

A. Optimization of Boundary Detection

The parameters of boundary detection should be tuned in this optimization are radiusStep , dmax , dmin , and thmin . The radiusStep , dmax , and dmin are the members

of integer set while thmin is the member of the real set. The information of the individual chromosome is listed in Table 1 while the configuration of GA parameters is listed in Table 2.

Table 1. Chromosome information for parameters of boundary detection

Parameter	Start Index	End Index	Length
radiusStep	1	5	5
dmax	6	9	4
dmin	10	13	4
thmin	14	24	11
Total			24

Table 2. Configuration of GA parameters for boundary detection

GA Parameter	Value
nind	27
ve	0.0741
vc	0.5
vm	0.5
N s	75
N max	1000

• B.    Optimization of Iterative-Splitting

There are four parameters of the iterative-splitting those should be optimized by a GA, i.e. splitStep , shortLengthSplit , shortRatioSplit , and longRatioSplit . Both splitStep and shortLengthSplit belong to the integer set while the rests belong to the real set. The chromosome information of the individual is summarized in Table 3.

Table 3. Chromosome information for parameters of iterative-splitting

Parameter Start Index End Index Length splitStep 1 10 10 shortLengthSplit 11 19 9 shortRatioSplit 20 38 19 longRatioSplit 39 57 19 Total 57 explained modified fitness function f and the GA parameter configuration. The configuration of parameters is listed in Table 4.

Table 4. Configuration of GA parameters for iterative-splitting

GA Parameter	Value
nind	50
ve	0.02
vc	0.25
vm	0.75
Ns	100
N max	1000

• C.    Optimization of Iterative-Assimilation

There are three parameters optimized in the iterative-assimilation procedure, i.e. maxFricativeRatio , averageFricativeRatio , and decresingResidualRatio . All parameters are real values. The information of the chromosome for encoding and decoding the parameters is shown in Table 5.

Table 5. Chromosome information for parameters of iterative-assimilation

Parameter	Start Index	End Index	Length
maxFricativeRatio	1	20	20
averageFricativeRatio	21	40	20
decresingResidualRatio	41	60	20
Total			60

Similar to the iterative-splitting optimization, the fitness function is slightly modified to get a better-focused area. The best deletion error referred E that previously obtained by splitting optimization is used as the basis of minimum value for the individual fitness with the tolerance level t . The modified fitness function for iterative-assimilation procedure f is computed using a formula

The optimization of the iterative-splitting is performed after the optimization of boundary detection. Hence, the best minimum insertion error E produced by the previous optimization is known. Using this information, the fitness function is modified to be

f asm

/ f , ^E 2 < ( ^Edel + t a ) 4 E 2 > ( E del + t a )

fsplit

' f , E , < ( E_ + t s ) = <

0, E i > ( E ins + t s )

to obtain a focused searching area for the optimization. A tolerance level t is used so that any individual with a fitness less than or equal to ( E_iro + t_s ) is considered as a bad solution.

As for the rest of the procedure, this optimization is using similar optimization like the boundary detection optimization. The difference lies in the previously

Finally, the configuration of the GA parameters for iterative-assimilation is listed in Table 6.

Table 6. Configuration of GA parameters for iterative-assimilation

GA Parameter	Value
nind	50
ve	0.04
vc	0.75
vm	0.25
Ns	100
N max	1000

• V.    Result and Discussion

This research uses a dataset of 110 Indonesian utterances spoken by one female speaker. This is the same dataset as used in [3]. There are 1,409 syllables with varying structures, from the simple structures, such as V, VC, and CVC, to the complex ones, such as CVCCC and CCVC, where C stands for a consonant while V for a vowel.

• A.    Optimization results for Boundary Detection

The experiment is performed using 9 observations of w1 and w2 from 0.1 to 0.9. Table 7 shows the optimization results for the boundary detection. The next optimization is carried out based on a minimum score using a formula score =

( E_{ + E₂

I 2

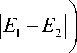
where E and E are the insertion and deletion errors respectively. Table 7 shows that w = 0.3 and w₂ = 0.7 is the optimum values those give the most balanced values of E and E producing the minimum score.

Table 7. Optimization results of boundary detection

w 1	w 2	E 1 (%)	E 2 (%)	Score
0.1	0.9	80.86	5.0541	118.763
0.2	0.8	35.10	12.70	46.30
0.3	0.7	14.63	18.40	20.285
0.4	0.6	11.47	20.17	24.52
0.5	0.5	2.85	27.33	39.57
0.6	0.4	2.54	27.87	40.535
0.7	0.3	1.69	29.33	43.15
0.8	0.2	0.92	31.72	47.12
0.9	0.1	0.69	33.03	49.065

An optimization process using the selected observation produces the optimum values of parameters shown in Table 8. These values will be used later for the proposed syllable segmentation method.

Table 8. Boundary Detection parameter value of the selected observation

Boundary Detection Parameter	Value
radiusStep	24
dmax	1
dmin	5
Thmin	1.2220

• B.    Optimization results for Iterative-splitting

The iterative-splitting optimization is performed for 5 observations since a splitting cannot decrease the deletion error but it just introduces a new boundary. Thus, the weight of the insertion beyond 0.5 is unnecessary. The optimization results are summarized in Table 9. These experiments are based on the previous results of boundary detection, where the optimum insertion and deletion errors are 14.63% and 18.40 respectively. The value of tolerance level t is adjusted to 15% so that the insertion errors bigger than 29.63% are discarded. The difference between an insertion error and the optimum one AEj as well as he difference between a deletion error and the optimum one AE2 are shown in the results. The optimum values of w and w are 0.1 and 0.9 respectively to maximally decrease the deletion error within the tolerance level of 15%.

Table 9. Optimization results for iterative-splitting

w 1	w 2	E 1 (%)	E 2 (%)	A E 1	A E 2
0.1	0.9	29.10	12.39	14.47	-6.01
0.2	0.8	28.10	12.55	13.47	-5.85
0.3	0.7	28.33	12.47	13.70	-5.93
0.4	0.6	26.56	13.01	11.93	-5.39
0.5	0.5	14.63	18.32	0	-0.08

• C.    Optimization results for Iterative-assimilation

The experiments on the optimization of iterative-assimilation are also performed for 5 observations like the iterative-splitting optimization. Since the iterative-assimilation cannot decrease the deletion error, the weight of the deletion beyond 0.5 is also unnecessary. The optimization results are listed in Table 10.

Table 10. Optimization results for iterative-assimilation

w 1	w 2	E 1 (%)	E 2 (%)	A E 1	A E 2
0.5	0.5	25.56	12.39	-3.54	0
0.6	0.4	25.25	12.39	-3.85	0
0.7	0.3	25.17	12.39	-3.93	0
0.8	0.2	25.17	12.39	-3.93	0
0.9	0.1	24.71	12.39	-4.39	0

Similar to the iterative-splitting, one of the five observations is selected based on a criterion. In this case, the criterion is a combination of the weights that gives the biggest reduction of insertion error. Hence, an observation with w = 0.9 and w₂ = 0.1 is selected since it reduces the insertion error up to 4.39% but does not increase the deletion error. This selected observation gives the parameter values of the iterative-assimilation as listed in Table 11.

Table 11. Iterative-assimilation parameter value of the selected observation

Iterative-assimilation Parameter	Value
maxFricativeRatio	1.6572
averageFricativeRatio	0.3155
decresingResidualRatio	1.3210

• D.    Results of Syllable Segmentation

Finally, all parameter values of the three optimizations are used to evaluate the proposed syllable segmentation procedure. In these experiments, five different types of segmentation are performed, i.e. 1) the segmentation using the boundary detection only (ALN); 2) the segmentation using boundary detection with iterative-splitting (ALNIS); 3) the segmentation using boundary detection with iterative-splitting and then iterative-assimilation (ALNISIA); 4) the segmentation using boundary detection and iterative-assimilation (ALNIA); and 5) the boundary detection with the non-iterative-splitting and non-iterative-assimilation procedure (ALNSA). The experimental results are summarized in Table 12.

Table 12. Results of syllable segmentation

Method	Accuracy (%)	Insertion (%)	Deletion(%)
ALN	83.04	14.63	18.40
ALNIS	88.57	29.10	12.39
ALNISIA	88.57	24.71	12.39
ALNIA	83.04	13.93	18.40
ALNSA	86.59	28.33	14.55

The ALN and ALNIA give the worst accuracy. But, ALNIA produces the lowest insertion error of 13.93% while the ALN gives 14.63%. It shows that the iterative-assimilation slightly reduces the insertion error by 14.63% - 13.93% = 0.70%.

Both ALNIS and ALNISIA give the best accuracy of 88.57% and the lowest insertion error of 12.39%. But, the ALNISIA gives the smallest insertion error of 24.71%. It means both iterative-splitting and iterative-assimilation work successfully in a good combination, where the accuracy does not decrease and the deletion error does not increase. It proves that the iterative-assimilation never over-merge the expected segments.

Finally, the ALNSA is compared to the ALNISIA. Using the same parameter obtained from the optimization, the ALNISIA gives the best accuracy and the smallest insertion error. The accuracy slightly increases by 1.98% and the deletion error slightly decreases by 2.16%. This concurs that the iterative-splitting gives a better performance in recovering the missed syllable segments. The iterative-assimilation also performs better than the non-iterative-assimilation, where it reduces the insertion by 3.62%. This implies that the iterative repetition of the assimilation procedure takes care of an assimilation that combines more than two fricatives. The comparison of the non-iterative-splitting and the iterative-splitting is shown in Table 13 while the comparison of the noniterative-assimilation and the iterative-assimilation is listed in Table 14.

Table 13. Comparison of non-iterative-splitting and iterative-splitting results

Method	Accuracy (%)	Deletion(%)
Non-Iterative-splitting	86.59	14.55
Iterative-splitting	88.57	12.39

Table 14. Comparison of non-iterative-assimilation and iterative- assimilation results

Method	Insertion (%)
Non-Iterative-assimilation	28.33
Iterative-assimilation	24.71

• VI.    Conclusion

A new model of automatic syllable speech segmentation based on a time-domain energy-based feature and an adaptive threshold has been successfully developed. The proposed GA-based optimization on parameters of the boundary detection, the iterative-splitting, and the iterative-assimilation works properly. The adaptive boundary detection gives the initial quite high accuracy as well as the low insertion and deletion errors. The iterative-splitting gives a higher accuracy and a smaller insertion error than the non-iterative-splitting. The iterative-assimilation produces a lower insertion error than the non-iterative-assimilation since it is capable of taking care of the assimilation of two fricatives or more. The sequential combination of both procedures gives the same accuracy and deletion error, but a smaller insertion error. It means the iterative-assimilation does not over-merge the expected syllable segments. Unfortunately, the iterative-assimilation just handles two fricatives or more in the left order. Hence, the iterative-assimilation can be carefully improved to handle the fricatives in the right order.

Acknowledgment

This work is supported by School of Computing, Telkom University, Bandung, Indonesia.