Optimum ECG signal filtering based on wavelet transformation

Автор: Saidov B.B., Telezhkin V.F.

Журнал: Вестник Южно-Уральского государственного университета. Серия: Компьютерные технологии, управление, радиоэлектроника @vestnik-susu-ctcr

Рубрика: Краткие сообщения

Статья в выпуске: 4 т.21, 2021 года.

Бесплатный доступ

The development of digital signal processing and microprocessor technology creates conditions for improving methods for diagnosing the functional state of organs. Wavelet analysis is a modern and promising method of information processing. In order to determine the effective optimal filtering of the electrocardiography signal based on the wavelet transform, wavelet filtering was performed using wavelets of different families, the efficiency of using different levels of decomposition, methods for calculating the threshold and types of the threshold function was investigated. Aim. Determination of effective optimal filtering of electrocardiography signal based on wavelet transform. Materials and methods. Cardiograms were taken for analysis. Then they were digitized and entered into a computer for processing. A program was written in the Matlab environment that implements continuous and discrete wavelet transform. Results. As a result of the research, 56 combinations of noise reduction parameters were tested for three noise levels. It was found that the maximum degree of signal purification from noise was obtained using the Coiflets 5 wavelet using a rigid thresholding method, with a heuristic method for calculating the threshold value. Wavelet Simlet 8 has lower correlation coefficient values than Coiflets 5, at 35 dB the best result is 97%, the noise level is 40 dB the best result is 98.7%, the noise level is 45 dB the best result is 99.3%, which is generally negligible differs from the correlation coefficients of the wavelet Coiflets 5. Conclusion. As a result of the study, the first and the present work, the following conclusions were made: the optimal level of the wavelet decomposition of the ECG signal N = 2; the maximum degree of signal cleaning from noise was obtained using the Coiflets 5 wavelet using a rigid thresholding method, with a heuristic method for calculating the threshold value; Simlet 8 wavelet using a soft thresholding method with a minimax thresholding method also shows noteworthy results, slightly inferior to Coiflets 5 wavelet results.

Еще

Ecg signal, wavelet simlet 8, wavelet coiflets 5, thresholding method, optimal level

Короткий адрес: https://sciup.org/147236497

IDR: 147236497 | DOI: 10.14529/ctcr210415

Текст краткого сообщения Optimum ECG signal filtering based on wavelet transformation

The development of means of digital signal processing and microprocessor technology create conditions for improving methods for diagnosing the functional state of organs [1–3]. Wavelet analysis is a modern and promising method of information processing. The wavelet analysis apparatus was developed in the early 1980 [4–6]. The results obtained in various fields using wavelet analysis have increased interest in this area and contribute to its continuous development [7–9].

Wavelet analysis can be successfully used to smooth and remove noise in the ECG signal. The cardio signal stripped of noise components, looks clearer, while its volume is from 10% to 5% of the original signal, which largely solves the problem of storing cardiac records [10–12].

To implement the procedure for the wavelet filtering of the CS, the method of threshold processing of the coefficients was chosen. In the course of the work, an algorithm for the wavelet filtering of the CS by the thresholding method was developed and implemented. There is a wide choice of wavelet bases used for filtering signals by the thresholding method, the choice of the wavelet function and noise reduction parameters, such as the type of threshold, the level of decomposition, etc., plays a decisive role in the operation of the method [13–15].

In order to determine the effective optimal filtering of the electrocardiography signal based on the wavelet transform, wavelet filtering was performed using wavelets of different families, the efficiency of using different levels of decomposition, methods for calculating the threshold and types of the threshold function was investigated.

Determination of the effective filter parameters

Let us determine the signal-to-noise ratio and the correlation coefficient for each set of parameters for the selected decomposition level N = 2.

Let's test 7 selected types of wavelet functions: Haar wavelet; Daubechies wavelet 4; Daubechies wavelet 6; Coiflets wavelet 5; wavelet Simlet 4; wavelet Simlet 6; wavelet Simlet 8.

For each type of wavelet, we use a hard or soft thresholding method. Let us calculate the threshold value by each of the four methods for calculating the threshold: adaptive, heuristic, logarithmic and minimax calculation method.

Thus, for the study, it is necessary to enumerate 56 variants of possible combinations of noise reduction parameters for each noise level.

The calculated data are presented in Tables 1, 2, each cell contains data for three noise levels SNR 1 = 35, SNR 2 = 40, SNR 3 = 45.

Consider the signal-to-noise ratio for all combinations of parameters; the calculation results are shown in Table 1.

Table 1

Signal-to-noise ratios for all combinations of parameters

Parameters	Soft method				Hard method
Parameters	rigrsure	sqtwolog	minimaxi	heursure	rigrsure	sqtwolog	minimaxi	heursure
	36.740	36.805	36.829	36.880	36.770	36.695	36.697	36.668
Haar	38.150	38.078	38.107	38.15	38.112	38.146	38.092	38.094
	38.620	38.619	38.638	38.64	38.634	38.626	38.642	38.621
	39.994	39.886	40.166	40.028	39.552	39.881	39.586	39.796
Simlet 4	43.372	42.971	43.47	43.223	43.115	43.258	43.298	43.137
	45.246	45.278	45.224	45.276	45.17	45.171	45.306	45.181
	39.964	39.716	39.836	39.669	39.614	39.505	39.877	39.673
Simlet 6	42.846	42.950	42.999	43.015	42.811	43.055	43.236	43.002
	44.643	44.733	44.755	44.603	44.734	44.657	44.681	44.683
	40.512	40.530	40.517	40.440	40.382	40.248	40.48	40.535
Simlet 8	44.033	44.264	43.906	44.23	44.149	43.838	44.054	43.946
	46.427	46.535	46.502	46.544	46.613	46.363	46.456	46.458
	39.958	40.079	40.058	39.994	39.751	40.273	40.021	40.16
Daubechies 4	43.430	43.400	43.446	43.616	43.273	43.582	43.222	43.237
	45.306	45.083	45.320	45.309	45.435	45.268	45.335	45.225
	39.619	39.446	39.643	39.804	39.957	40.135	40.039	39.904
Daubechies 6	43.031	42.978	43.194	43.108	43.153	43.005	43.237	42.821
	45.057	44.874	44.871	44.937	44.961	44.893	44.934	44.970
	40.575	40.102	40.001	40.440	40.525	40.279	40.290	40.770
Coiflets 5	43.865	43.634	44.022	43.764	44.192	44.025	44.236	44.404
	46.828	46.975	46.697	46.811	46.832	46.642	46.655	46.863

As a result of the analysis of the obtained data on the signal-to-noise ratios of all combinations of parameters, it was revealed:

– the least effective wavelet for filtering ECG signals is the Haar wavelet;
– the most optimal wavelet from the Simlet family – Simlet 8;
– Daubechies 4 wavelet has a higher signal-to-noise ratio for all noise levels than Daubechies 6 wavelet;
– Simlet 8 and Coiflets 5 wavelets have the highest signal-to-noise ratios among the considered wavelets.

Consider the correlation coefficients for all combinations of parameters, the calculation results are shown in Table 2.

Table 2

Correlation coefficients for all combinations of parameters

Parameters	Soft method				Hard method
Parameters	rigrsure	sqtwolog	minimaxi	heursure	rigrsure	sqtwolog	minimaxi	heursure
	92.4	92.5	92.6	92.5	92.5	92.3	92.4	92.4
Haar	94.5	94.4	94.4	94.5	94.4	94.5	94.4	94.4
	95.0	95.0	95.1	95.1	95.1	95	95.1	95
	96.5	96.4	96.6	96.6	96.2	96.5	96.2	96.4
Simlet 4	98.4	98.3	98.4	98.4	98.3	98.3	98.4	98.3
	98.9	99	98.9	99.0	98.9	98.9	99.0	98.9
	96.5	96.4	96.5	96.3	96.3	96.2	96.3	96.3
Simlet 6	98.2	98.2	98.3	98.2	98.2	98.2	98.3	98.3
	98.8	98.8	98.8	98.8	98.8	98.8	98.8	98.8
	97.0	96.8	97.0	96.9	96.9	96.7	96.9	97
Simlet 8	98.6	98.7	98.6	98.7	98.7	98.5	98.6	98.6
	99.2	99.2	99.2	99.2	99.2	99.2	99.2	99.2
	96.5	96.6	96.6	96.6	96.3	96.8	96.6	96.7
Daubechies 4	98.4	98.4	98.4	98.5	98.3	98.4	98.3	98.3
	99.0	98.9	99.0	99.0	99.0	98.9	99.0	98.9
	96.3	96.1	96.3	96.5	96.4	96.7	96.7	96.5
Daubechies 6	98.3	98.2	98.3	98.3	98.3	98.2	98.3	98.1
	98.9	98.8	98.8	98.9	98.9	98.9	98.9	98.9
	97.0	96.6	96.5	96.9	96.9	96.7	96.8	97.2
Coiflets 5	98.6	98.6	98.6	98.5	98	98.6	98.7	98.7
	99.3	99.3	99.2	99.3	99.3	99.2	99.2	99.3

As a result of the analysis of the obtained data on the correlation coefficients for all combinations of parameters, it was revealed:

– filtering using the Haar wavelet showed the worst results;
– the most optimal wavelet from the Simlet family – Simlet 8;
– Daubechies 4 wavelet at all noise levels has better correlation coefficients than Daubechies 6;
– The highest correlation coefficients were obtained as a result of filtering with Simlet 8 and Coiflets 5 wavelets.

After considering and generalizing the conclusions made on the calculated signal-to-noise ratios and correlation coefficients, two wavelets that filter the ECG signal most effectively were identified: Simlet 8 and Coiflets 5.

To visualize the collected data and identify the optimal set of parameters for each of the two identified wavelets, a graphical data analysis program was written. Figs. 1, 2 show the result of the graphical data analysis program.

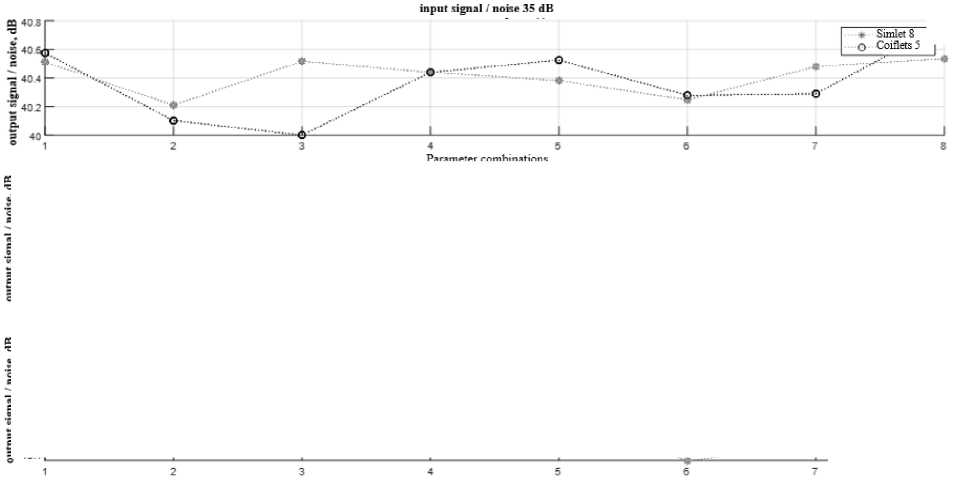
F ig. 1 shows a comparison of the output signal-to-noise ratios of Simlet 8 and Coiflets 5 wavelets for eight combinations of parameters presented in Table 1. The figure shows three graphs for three noise levels SNR 1 = 35, SNR 2 = 40, SNR 3 = 45.
F ig. 2 shows a comparison of the correlation coefficients of the Simlet 8 and Coiflets 5 wavelets for eight combinations of parameter parameters presented in Table 2. The figure shows three graphs for three noise levels SNR 1 = 35, SNR 2 = 40, SNR 3 = 45.

As a result of the graphical analysis of the collected data, it was revealed:

– The highest output signal-to-noise ratio for all considered noise levels has the Coiflets wavelet 5 using a rigid thresholding method, with a heuristic method for calculating the threshold value;
– for most sets of parameters the values of the signal-to-noise ratio of the wavelet Coiflets 5 exceed the values of the signal-to-noise ratio of the wavelet Simlet 8, which is especially clearly seen for the input noise level of 45 dB;
– The largest values of the correlation coefficient for all considered noise levels (97.2%, 98.7%, 99.3%) have the Coiflets 5 wavelet using a rigid thresholding method, with a heuristic method for calculating the threshold value;
– Simlet 8 wavelet has lower correlation coefficient values than Coiflets 5, at a noise level of 35 dB the best result is 97%, a noise level of 40 dB is the best result 98.7%, a noise level of 45 dB is the best result 99.3%, which, in general, slightly different from the correlation coefficients of the wavelet Coiflets 5;
– Simlet 8 wavelet shows good filtering results using soft thresholding method, with minimax thresholding method.

Parameter combinations

Fig. 1. Comparison of the output signal-to-noise ratios of Simlet 8 and Coiflets 5 wavelets for eight combinations of parameters

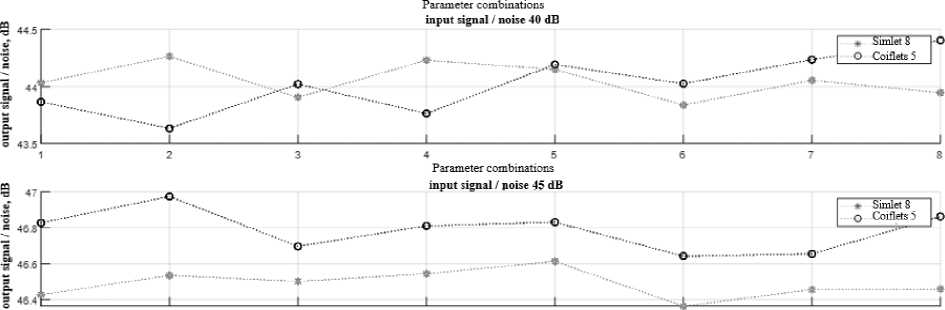
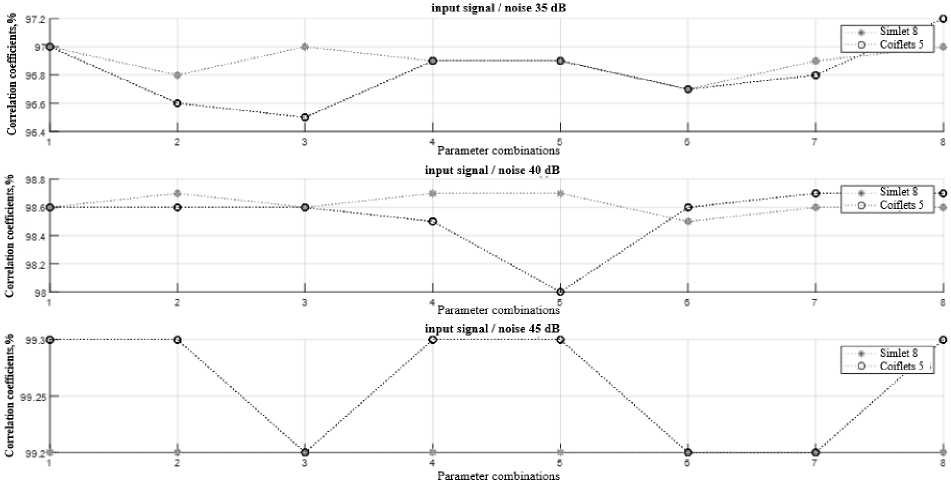
Fig. 2. Comparison of the correlation coefficients of wavelets Simlet 8 and Coiflets 5 for eight combinations of parameters

As a result of the research, 56 combinations of noise reduction parameters were tested for three noise levels. It was found that the maximum degree of signal purification from noise was obtained using the Coiflets 5 wavelet using a rigid thresholding method, with a heuristic method for calculating the threshold value.

Conclusion

As a result of the study, the following conclusions were made: optimal level of wavelet decomposition of ECG signal N = 2; the maximum degree of signal purification from noise was obtained using Coiflets 5 wavelet using a rigid thresholding method, with a heuristic method for calculating the threshold value; Simlet 8 wavelet using a soft thresholding method, with a minimax thresholding method, also shows noteworthy results, slightly inferior to the Coiflets 5 wavelet results.

Список литературы Optimum ECG signal filtering based on wavelet transformation

Bohan C., Hongliu, Y. ECG Signal Processing and Human State Detection Based on Wearable Electrodes. Journal of Physics: Conference Series, 2021, pp. 1-8. DOI: 10.1088/1742-6596/1952/3/032055
Saidov B., Telezhkin V. Transformation of the Amplitude-Modulated Spectrum of a Signal on a Nonlinear Element. 2020 International Russian Automation Conference (RusAutoCon), 2020, pp. 757-761. DOI: 10.1109/RusAutoCon49822.2020.9208134
Phinyomark A., Limsakul C., Phukpattaranont P. An Optimal Wavelet Function Based on Wavelet Denoising for Multifunction Myoelectric Control. 6th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON 2009), Thailand, 2009, vol. 2, pp. 1098-1110. DOI: 10.1109/ECTIC0N.2009.5137236
Burhan E. Signal and Image Denoising Using Wavelet Transform. Advances in Wavelet Theory and Their Applications in Engineering, Physics and Technology, 2012, pp. 495-514. DOI: 10.5772/36434
Singh B.N., Tiwari A.K. Optimal Selection of Wavelet Basis Function Applied to ECG Signal Denoising. Digital Signal Processing, 2006, vol. 16 (3), pp. 275-287. DOI: 10.1016/j.dsp.2005.12.003
Bagheri F., Ghafarnia N., Bahrami F. Electrocardiogram (ECG) Signal Modeling and Noise Reduction Using Hopfield Neural Networks. Eng. Technol. Appl. Sci. Res., 2013, vol. 3, no. 1, pp. 345-348. DOI: 10.48084/etasr.243
Sameni R., Shamsollahi M.B., Jutten C., Babaie-Zadeh M. Filtering noisy ECG signals using the extended kalman filter based on a modified dynamic ECG model. Computers in Cardiology, 2005, pp. 1017-1020. DOI: 10.1109/CIC.2005.1588283
Shemi P.M., Shareena E.M. Analysis of ECG signal denoising using discrete wavelet transform. 2016 IEEE International Conference on Engineering and Technology(ICETECH), 2016, pp. 713-718, DOI: 10.1109/ICETECH.2016.7569341
Chouakri S.A., Bereksi-Reguig F., Ahmaïdi S., Fokapu O. Wavelet Denoising of the Electrocardiogram Signal Based on the Corrupted Noise Estimation. Computers in Cardiology, 2005, pp. 1021-1024. DOI: 10.1109/CIC.2005.1588284
Telezhkin V., Saidov B. Integrated Information Processing in Wireless (Secure) Communications of Corporate Communication Systems. 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), 2020, pp. 1-5. DOI: 10.1109/FarEastCon50210.2020.9271417
Sameni R., Shamsollahi M.B., Jutten C., Clifford G.D. A Nonlinear Bayesian Filtering Framework for ECG Denoising. IEEE Transactions on Biomedical Engineering, 2007, vol. 54, no. 12, pp. 2172-2185. DOI: 10.1109/TBME.2007.897817
Mishu M.M.H., Hossain A.B.M.A., Emon M.E.A. Denoising of ECG signals using dual tree complex wavelet transform. 2014 17th International Conference on Computer and Information Technology (ICCIT), 2014, pp. 379-382. DOI: 10.1109/ICCITechn.2014.7073141
Aowlad Hossain A.B.M., Haque M.A. Analysis of Noise Sensitivity of Different ECG Detection Algorithms. International Journal of Electrical and Computer Engineering (IJECE), 2013, vol. 3, no. 3, pp. 307-316. DOI: 10.11591/ijece.v3i3.2516
Omid S., Mohammad B.Sh. ECG Denoising and Compression Using a Modified Extended Kalman Filter Structure. IEEE transactions on biomedical engineering, 2008, vol. 55, no. 9, pp. 22402248. DOI: 10.1109/TBME.2008.921150
Telezhkin V., Saidov B., Ragozin A. Recognition and Elimination of Anomalies in Information Leakage Channels in Opto-Ultrasonic Communication Channels in Data Streams of Industrial Automated Systems. 2021 International Russian Automation Conference (RusAutoCon), 2021, pp. 201-206. DOI: 10.1109/RusAutoCon52004.2021.9537495

Еще

Краткое сообщение