Option Pricing Under Stochastic Interest Rates

Published Online June 2012 in MECS

Available online at

• 1.    Introduction

  Black, Scholes (1973) and Merton[2] (1973) showed in their seminal papers that a derivative security can be priced by creating a replicating portfolio, i.e. a portfolio of primitive securities which matches the payoff of the derivative at maturity. Since both the replication portfolio and the derivative offer the same payoff at maturity, they have to have the same price at any preceding time. Deviations from this equality lead to arbitrage possibilities. Hence, the pricing by duplication procedure inhibits arbitrage by construction. Since then the field of financial engineering has grown phenomenally. The Black– Scholes–Merton risk neutrality formulation of the option pricing theory is attractive because the pricing formula of a derivative deduced from their model is a function of several directly observable parameters (except one, which is the volatility parameter). The derivative can be priced as if the market price of the underlying asset’s risk is zero.

• 2.    European option pricing Formula

Detemple[8](2005) reviewed the valuation of American options. Several semi-analytical approximations for American option prices have been proposed in the literature (Barone Adesi and Whaley[1], 1987; Broadie and Detemple[5], 1996; Bunch and Johnson[6], 2000). Although these approaches are fast and accurate, they can not easily be extended beyond the Black-Scholes model. It has been firmly established that the Black-Scholes model is not consistent with quoted option prices. The literature advocates the introduction of stochastic volatility or jump store produce the implied volatility smile observed in the market. The introduction of an additional stochastic volatility factor enormously complicates the pricing of American options. Presently, this can only be done by means of numerical schemes, which involve solving integral equations(Kim[16],1990; Huang, Subrahmanyam, and Yu[13], 1996; Sullivan[20],2000; Detemple and Tian[9],2002), performing Monte Carlo simulations(Broadie and Glasserman[4], 1997; Longstaff and Schwartz[17],2001; Rogers[19], 2002;

* Corresponding author.

Haugh and Kogan[12],2004), or discrete the partial differential equation(Brennan and Schwartz[3], 1977; Clarke and Parrott[7], 1999; Ikonen and Toivanen[15], 2007). The early exercise premium of the American put option depends on the cost of carry determined by interest rates. Consequently, the volatility of interest rates does affect the decision to exercise this option at any point in time. This fact is recognized in the literature dealing with models with stochastic interest rates(Ho,Stapleton, and Subrahmanyam[11], 1997; Menkveld and Vorst[18],2001;Detemple and Tian[9], 2002). This literature, however, considers only two-factor extensions of the Black-Scholes model assuming that the volatility of the underlying asset is constant.

In this paper, we assume that the interest rate subject to a given Vasicek stochastic differential equations , by using martingale method to study the stochastic interest rate model of European option pricing and obtain the pricing formula.

The paper is organized as follows. In Section 2 we describe the assumptions of the option model, using martingale method, by solving a second order parabolic partial differential equation, we obtain the European option pricing formula. In Section 3 we compare the differences between the standard European option pricing formulas and European option pricing formula under stochastic interest rate .

The standard BS model makes the following assumptions: the market is frictionless (i. e. no transaction costs or taxes and no penalties for short selling); the market operates continuously, the risk-free interest rate r is a known constant; the asset X price t follows Geometrical Brownian Motion(GBM) with constant volatility σ > 0 and pays no dividends; options and

X derivatives are European (i. e. no early exercise) and expire at time T with a payoff that depends only on T ; the market is arbitrage free.

X

Under the assumption of GBM, the asset price t satisfies a stochastic differential equation (sde) of the form dXt — X (^dt + CTdBt)  Xo = x0

, where ^ is the growth rate of the asset. The term Bt is a standard Brownian motion under a measure P (called the real-world measure).

Theorem 1 (Ito’s Lemma) Let X t satisfy the sde dX t   ^{a ( xt} ) ^{dt + в ( x} , t ) dB¹ where x X and let V ⁽ x , t ) be any

• ^2,1    function. Then V ( X ^t , t ) satisfies the sde

dv — V + aVx + -в^хх dt + PVxdBt t         x        '      xx           ' x t where subscripts on V denote partial derivatives. It is sometimes more instructive to write this last sde in the equivalent form dv — V +-^V dt + VxdXt t               xx             x     t

Itô’s Lemma is the main tool used to solve sde’s. For example, the sde (1) for GBM can be solved by taking 1 2

Y /^^ x -^^ (   / x               Y              dY^ — (^     ct ) dt + CTdB_t

• ^{t t}      g ^{t 0} . The sde for ^t then becomes              2                 , and this is readily integrated to give

the representation

d

X, — x, exp {( ^ - - CT ²) t } + CT tZZ    Z □ N (0,1)

X

Now, let’s deduce the euro-options pricing formula under stochastic interest rate. Assume the asset price ^t satisfies

GBM dX

----= rdt + ст, ( r , t ) dB

_Xt        t          1 t         t

The interest rate is given by Vasicek Model[21]

dr = a ( 9 — r ) dt + c ₂ ( r , t ) dB 2

,     {B1 : t > 0} {B,2 : t > 0}       .   ,   , „ where t        , t        are standard Brown motions, cov( dB,', dB,2) = pdt  (| p < 1)

Let V  ^{V (} X ’ r’ t ) denote the price of the call European option,

^{V   ( X} t   K ) , K is the strike price.

We will find the option price. Using ^A and obtain the portfolio

hedging technical we derive function V ( X ^t , r ^t , t ) satisfy the appropriate sde,

П t = V —A , , x , — A 2 , p ,

Choose ^A 1 t share of stock and ^{A 2} t share of zero-coupon , the portfolio ^П t is risk-free in the period [ t , t ^{+ dt ]} .It’s also mean if choose appropriate ^A 1 t and ^{A 2} t , then we can get

d П = dV, — Aj _tdX_t — A₂ dP, which is risk-free, and then

,

d П _t = г , П _tdt = r [V, - A 1 X, — A₂ ,P, ] dt

P = P ( r , t ; T ).

Here ^tt ,      is the price of zero-coupon , and satisfies a stochastic differential equation (sde) of the form[22]

dP

-=- = rdt — X_v ( t ^cdB,

(Vasicek Model)

or

dP

-= = rdt — X_c .( t С r_tdB_t

(C-I-R Model).

By Itô’s Lemma, (4) can be written as

FdV 1  2v2d2V         v d2V 1  2d2V 1, dП, = — + -c.X —7+ ССРX---+ -a,—r dt t     dt   2  1    dx 2    1 2    dxdr  2  2 dr2

(d V Id X

—

(ay

A, I dX, + 1

1 t             t

J      V dr

—

к 5P L

^A 2 -T" I ^d r t d r )

_A  ( d P  1 2 d ² P I

—

A₂,    + -cdt

• ² t V d t    2    2 d r ² J

  
  

The third term of the right equation can be substitute as

( „   _ a p, I,

• —A₂ rP — a( 9 — r —) dt

2 t

V            d r J

In order to eliminate the risk, let d v A , a v ,a>p — = A., A2, = —/ — dx 1 t 2 t at ar

, , considering (7) and (2), we obtain дV 1 2v2 д2V        д VV   1 2 d2V

--1— a, X —— + ^л2 p X--1— <79 —— + rX — д t 2 1    дX2    1 2 дX д r 2 2 д r2

.. .ar _      . __

+ a ( 0 — r )-- rV = 0    ( r €□ , X eD⁺ , t e [0, T ])

'       - дr                     '        '' as t = TV (X, t, T) = (X — K)+   (r €□ , X eD+ )

as,

We know by the martingale method option pricing theory[10], there exist a martingale measure Q, such that

V, = E^q I e ^—^ ' r ^{Td T} ( X_T — K ) ⁺ | r ( t ) = r , X ( t ) = X_t |

^{V                                      7}                                                       (10)

л                             .              P = P(rd ; T )                         .

To transform valuation of unit of account , that zero-coupon ^tt , as a new unit of account , and a corresponding price system introduced

X L, V t = V p      p

Based on unit conversion valuation theory, the equivalent martingale measure exists , such that ( 10) can be rewritten as

U

V = e^q

(V t | r ( t ) = r t , X ( t ) = X t )

U = E^QU

—

Г к I p (t) = p, x (t) = x,

= E Q U | ( X t — K ) ⁺ P ( t ) = P, , X ( t ) = X,

P = 1

In the last equation, we use the fact ^T .

X

(12) showed that the proceeds at the time T , function V ^t can be transformed into only depends on ^t . In the Vasicek dP

—L = r.dt — M (t )QdB, Ptt model, zero-coupon price processes satisfies stochastic differential equation, t

d In p = rt so,            L

—

1 < r ₂ ² X 2 ( t ) dt — < r₂ X_v ( t ) dB²

According to (1),

d In X_t = r_t

t

—

— ^ ² dt + ^ dB ²

2   1             1

X t = Xt-

P

As for         t ,such that d In Xt = d In X — d In p

= 1 [ ct₂ ² X ² ( t ) — ^ ² ] dt + ^ dB 1 + ^ X ( t ) dB²

This shows that for the Vasicek model, the stochastic differential equations of X ^t is no longer significant contain with

Xr t and t , so we can put (12) rewritten as

V t = E Q I ( X T - K ) + X ( t ) = X t

к         г                    f   { X t , V t }                i v V t — V ( X t , t )i

This shows that for the new price system        ^t , function correlation ^t            holds.

To solve problem (8) and (9), we draw a new transformation of independent variables, X y — —--—

P ( r , t ; T )

and a new unknown function denotes as

V ( y , t) —

V ( X , r , t ) P ( r , t ; T )

According to primarily computations,

d V ,.PP  dV^v   d V d P

- — v —+ p--y-- dt     dt     dt     dy dt dV  dPP   dV dP

-- — V--y dr    dr    dy dr dV _8V_ dX ~ dy d2V „P2P   dV d2P 2 d2 V 1 (dPY

— V       yy         I     I dr2     dr2    dy dr2     dy P ^ dr )

d 2 V       d ² V 1 d P

— - y dr dX     dy2 P dr d2V _ 1 d2 V dX? ~ P dy?

P ( r , t ; T )

Substitute them into (8), and divided by           , such that

d V  1

1 d t   2

2 X ²

—

„      X d P  1  _{2 2} ( 1 d P ^ ²

2 ct^tP ---+ — < r₂ y--

¹² P d r  2 ²   ( P d r j

d ² V d y y

1   d P

+

P d t

a_T ² d ² P

2 d r ²

d P  X

+ a ( 0 — r )-- r — d r   y

d V

y dy

+1 d P P "d t"

ct₂ ² d ² P

d r ²

. dP

+ a( 0 — r )-- rP V — 0

d r

Considering transformation (13) and the function problem

P ( r , t ; T )

satisfies the following second order parabolic pde’ s Cauchy

^{d P} + ^- ^d-^P + a ( 0 — r ) ^{d P} — rP — 0  ( r eD , t e [0, T ])

¹ dt 2 d r¹             d r

_ P ( r , T ) — 1.

<

Then, we immediately find that function V ( y , t ) satisfies the equation

5 r  2        d y

, v ( у , t ) = V(X|r,Tr = ( у - к)+ and the definitely solution condition is            P(r,T; T)

where K is the option’s strike price,

a ( t ) = ^a¹ + 2 paa x ( t ) + a ₂ ² x ² ( t )

X ( t ) = - 7 I P

P d r

The solution of problem (15) can be expressed by the general Black-Scholes formula

V ( У , t ) = yN ( d i ) - KN ( d 2 )

T 2

d2 = dx - J a (r)dr t

Reverse to the original variables X , r , t and unknown function V by the transformation (13) and (14), such that (16) and (17) become

V ( X , r , t ) = P ( r , t ; T ) V | —-, t I ( P ( r , t ; T )   )

=X N ( d J ) - KP ( r , t ; T ) N ( d ₂)

X                 1 ^{T 2}

In--In P ( r, t ; T ) + — [ a ( r ) d r d ² = _JK ------,       ^{2 J t}---------

T 2

This formula was first proposed by Merton in 1973, when he was not received the random model of short-PP term interest rate r , but directly starting from the zero-coupon t , assuming t to meet the geometric Brownian motion, under the martingale measure, it is described by the following Stochastic differential equations,

dP            1

= rdt + a dBt where {Bt : t - 0} is standard Brown motion, aP is the zero-coupon’s (bonds) volatility.

Thus, European call option pricing formula is

V ( X , P , t )=X N ( d J ) - KPN ( d₂)

which

X1

ln - ln P + σ ( τ ) d τ

• *= K2

• 3. Conclusions

σ (τ)dτ t d =d -

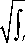
σ ( τ ) d τ

Compared with the standard European option pricing formula and European option under stochastic interest rate, there - r ( T - t )

are only two differences: one is zero-coupon replaced by e      ; another is that using σ instead of stock price volatility

σ ¹ . Except that the pricing formulas is exactly the same form .

Analysis from the actual markets, σP   σ1 means zero-coupon’s (bonds) volatility is far smaller than stock market’s volatility, but in general PP, P is monotonic decreasing, and t→T          . σ and 1 in fact has the minor difference. Because in general, stock prices and bond prices are positively correlated, then ρ > 0 . Therefore, ifσP < 2ρσ1 , by equation (24) we know σσ1 holds. Therefore under stochastic interest rates, the price of an option but have slightly decreased.

If a short-term interest rate model is given, only for the Vasicek model and Hull-White model[14], European option pricing formula has a simple form of the Merton formula (23). For C-I-R model, the corresponding zero-coupon stochastic

r model, the fluctuations in the rate of entry also including t , so it can not write (22), so by pricing unit conversion of lower dimension than Number of purposes, such as lost that possible style of (24).